Assets can be real or financial. Securities, like shares and bonds or debentures are called financial assets, while physical assets, like plant and machinery, are called real assets. The concepts of return and risk, as the determinants of value, are as fundamental and valid to the valuation of securities as to that of physical assets. We must clarify at the outset that there is no easy way to predict the prices of shares and bonds and thus, to become rich by a superior performance in the stock exchange. The unpredictable nature of the security prices is, in fact, a logical and necessary consequence of efficient capital markets. Efficient capital market implies a well-informed, properly functioning capital market. We can show why some securities are priced higher than others by using the concept of present value. This will help the financial managers to know the variables, which influence the security prices. They can then design their investment and financing activities in a manner, which exploits the relevant variables to maximize the market value of shares.
It should also be noted that ordinary shares are riskier than bonds (or debentures), and also that some shares are more risky than others. It, therefore, naturally follows that investors would commit funds to shares only when they expect that rates of return are commensurate with risk. We know from our earlier discussion in chapter 3 that the present value formulae are capable of taking into account both time and risk in the evaluation of assets and securities. For the purpose of our discussion, we shall assume risk as known. A detailed analysis of risk has been deferred to chapter 5.
CONCEPTS OF VALUE
Book Value
How are bonds and shares valued?1 What is the role of earnings per share (EPS) and priceearnings (P/E) ratios in the valuation of shares? EPS and P/E ratios are the most frequently used concepts by the financial community. Do they really have significance in the valuation of shares? Let us emphasize that the present value is the most valid and true concept of value. There are many other concepts of value that are used for different purposes. They are explained below.
Book value is an accounting concept. Assets are recorded at historical cost, and they are depreciated over years. Book value may include intangible assets at acquisition cost minus amortized value. Thus, the book value of an asset is its depreciated or amortized value. The book value of debt is stated at the outstanding amount. The difference between the book values of assets and liabilities is equal to shareholders’ funds or net worth. Book value per share is determined as net worth divided by the number of shares outstanding. Book value reflects historical cost, rather than value. Value is what an asset is worth today in terms of its potential benefits.
Replacement Value
Replacement value is the amount that a company would be required to spend if it were to replace its existing assets in the current condition. Thus, replacement value is conceptually superior to the book or historical value. It is difficult to find value of assets currently being used by the company. Replacement value is also likely to ignore the benefits of intangibles and the utility of existing assets. Hence, it does not reflect the real worth of assets.
Liquidation Value
Liquidation value is the amount that a company could realize if it sold its assets, after having terminated its business. It would not include the value of intangibles since the operations of the company are assumed to cease. Liquidation value is generally a minimum value, which a company might accept if it sold its business.
Going Concern Value
Going concern value is the amount that a company could realize if it sold its business as an operating business. Going concern value would always be higher than the liquidation value, since it reflects the future value of assets and value of intangibles.
Market Value
Market value of an asset or security is the current price at which the asset or the security is being sold or bought in the market. Market value per share is expected to be higher than the book value per share for profitable, growing firms. A number of factors influence the market value per share, and therefore, it shows wide fluctuations. What is important is the long-term trend in the market value per share. In ideal situation, where the capital markets are efficient and in equilibrium, market value should be equal to present (or intrinsic) value of a share.
Check Your Concepts
- Define book value and replacement value. What is the difference between them?
- Define and compare going concern value and liquidation value.
- What is market value? Is it different from the present value?
FEATURES OF A BOND OR DEBENTURE
The main features of a bond or debenture are discussed below.
A bond is a long-term debt instrument or security. Bonds issued by the government do not have any risk of default. The government will always honour obligations on its bonds. Bonds of the public sector companies in India are generally secured, but they are not free from the risk of default. The private sector companies also issue bonds, which are also called debentures in India. A company in India can issue secured or unsecured debentures. In the case of a bond or debenture, the rate of interest is generally fixed and known to investors. The principal of a redeemable bond or bond with a maturity is payable after a specified period, called maturity period.
Face value
Face value is called par value. A bond (debenture) is generally issued at a par value of `100 or `1,000, and interest is paid on face value.
Interest rate
Interest rate is fixed and known to bond-holders (debenture-holders). Interest paid on a bond/debenture is tax deductible. The interest rate is also called coupon rate. Coupons are detachable certificates of interest.
Maturity
A bond (debenture) is generally issued for a specified period of time. It is repaid on maturity. Thus, a bond/debenture with a maturity is called redeemable bond/ debenture.
Redemption value The value that a bond-holder (debenture-holder) will get on maturity is called redemption, or maturity, value. A bond (debenture) may be redeemed at par or at a premium (more than par value).
Market value
A bond (debenture) may be traded in a stock exchange. The price at which it is currently sold or bought is called the market value of the bond (debenture).
Market value may be different from par value or redemption value.
BOND VALUES AND YIELDS
It is relatively easy to determine the present value of a bond since its cash flows and the discount rate can be determined without much difficulty. If there is no risk of default, then there is no difficulty in estimating the cash flows associated with a bond. The expected cash flows consist of annual interest payments plus repayment of principal. The appropriate capitalization, or discount rate would depend upon the risk of the bond. The risk in holding a government bond is less than the risk associated with a debenture issued by a company. Consequently, a lower discount rate which may be equal to the risk-free rate would be applied to the cash flows of the government bond and a higher rate to the cash flows of the company debenture. Thus, the required rate of return of a bond is given as follows:
Bond’s required rate of return = Risk-free rate + risk premium on risky bond
Bonds may be classified into three categories: (a) bonds with maturity, (b) pure discount bonds and (c) perpetual bonds.
Bonds with Maturity (Redeemable Bonds)
The government and companies mostly issue bonds that specify the interest rate (coupon) and the maturity period. The present value of a bond (debenture) is the discounted value of its cash flows. The discount rate is the interest rate that investors could earn on bonds with similar characteristics. By comparing the present value of a bond with its current market value, it can be determined whether the bond is overvalued or undervalued. Let us consider Illustration 4.1.
ILLUSTRATION 4.1: Value of Bond with Maturity
The investor will receive cash `70 as interest each year for 5 years and `1,000 on maturity (i.e., at the end of the fifth year). We can thus determine the present value of the bond (B0) as follows
Suppose an investor is considering the purchase of a five-year, `1,000 par value bond, bearing a nominal rate of interest of 7 per cent per annum. The investor’s required rate of return is 8 per cent. What should he be willing to pay now to purchase the bond if it matures at par?
70 70 70 70 70 1,000
B0 (1.08)1 (1.08)2 (1.08)3 (1.08)4 (1.08)5 (1.08)5
It may be observed that `70 is an annuity for 5 years and `1,000 is received as a lump sum at the end of the fifth year. Using the present value factors, the present value of bond is:
B0 70 × 3.993 1,000 × 0.681 279.51 681 `960.51
This implies that `1,000 bond is worth `960.51 today if the required rate of return is 8 per cent. The investor would not be willing to pay more than `960.51 for bond today. Note that `960.51 is a composite of the present value of interest payments, `279.51 and the present value of the maturity value, `681.
Since most bonds will involve payment of an annuity (equal interest payments each year) and principal at maturity, we can use the following formula to determine the value of a bond: Bond value = PV of an annuity of interest + PV of maturity value
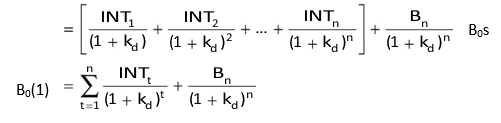
Notice that B0 is the present value of a bond (debenture), INTt is the amount of interest in period t (from year 1 to n), kd is the market interest rate or the bond’s required rate of return, Bn is bond’s terminal or maturity value in period n and n is the number of years to maturity.
In Equation (1), the right-hand side consists of an annuity of interest payments that are constant (i.e., INT1 = INT2… INTt) over the bond’s life and a final payment on maturity. Thus, we can use the annuity formula to value interest payments as shown below:
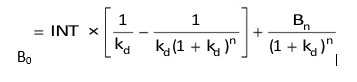
Yield-to-Maturity
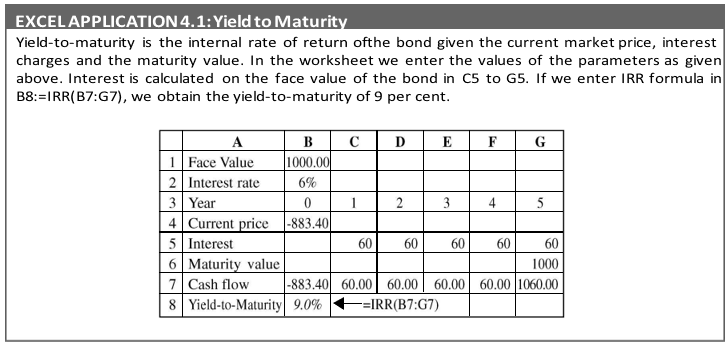
We can calculate a bond’s yield or the rate of return if its current market price and cash flows are known. Suppose the market price of a bond is `883.40 (face value being `1,000). The bond will pay interest at 6 per cent per annum for 5 years, after which it will be redeemed at par. What is the bond’s rate of return? The yield-to-maturity (YTM) is the measure of a bond’s rate of return that considers both the interest income and any capital gain or loss. YTM is bond’s internal rate of return. YTM of 5-year bond, paying 6 per cent interest on the face value of `1,000 and currently selling for `883.40 is 10 per cent as shown below:

It is, however, simpler to calculate a perpetual bond’s YTM. It is equal to interest income divided by the bond’s price. For example, if the rate of interest on `1,000 par value perpetual bond is 8 per cent, and its price is `800, its YTM will be:
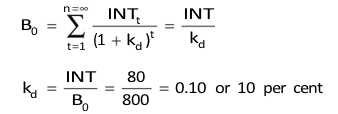
Current Yield
Yield-to-maturity is not the same as the current yield. Current yield is the annual interest divided by the bond’s current value. In the example, the annual interest is `60 on the current investment of `883.40. Therefore, the current rate of return or the current yield is: 60/883.40 = 6.8 per cent. Current yield considers only the annual interest (`60 in the example) and does not account for the capital gain or loss. On maturity, the bond price will increase to `1,000 and there would be a capital gain of `116.60 [`1,000 – `883.40]. Thus bond’s overall rate of return over 5 years period would be more than the current yield. If the bond’s current price were less than its maturity value, its overall rate of return would be less than the current yield.
Yield-to-Call
A number of companies issue bonds with buy back or call provision. Thus, a bond can be redeemed or called before maturity. What is the yield or the rate of return of a bond that may be redeemed before maturity? The procedure for calculating the yield-to-call (YTC) is the same as for YTM. The call period would be different from the maturity period and the call (or redemption) value could be different from the maturity value. Consider an example.
Suppose the 10 per cent, 10-year, `1,000 bond is redeemable (callable) in 5 years at a call price of `1,050. The bond is currently selling for `950. What is bond’s yield-to-call? The bond’s YTC is:
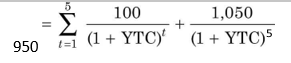
You can solve for YTC through trial and error or use a financial calculator. YTC is 12.7 per cent. Suppose the bond will be redeemed at `1,050 on maturity. What is the YTM? It is given as follows:
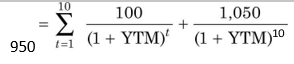
Bond Value and Amortization of Principal
A bond (debenture) may be amortized every year, i.e., repayment of principal every year rather than at maturity. In that case, the principal will decline with annual payments and interest will be calculated on the outstanding amount. The cash flows of the bonds will be uneven. Let us consider Illustration 4.2.
ILLUSTRATION 4.2: Value of a Bond When Principal is Amortized Each Year
The government is proposing to sell a 5-year bond of `1,000 at 8 per cent rate of interest per annum. The bond amount will be amortized (repaid) equally over its life. If an investor has a minimum required rate of return of 7 per cent, what is the bond’s present value for him?
The amount of interest will go on reducing because the outstanding amount of bond will be decreasing due to amortization. The amount of interest for five years will be: `1,000 × 0.08 = `80 for the first year; (`1,000 – `200) × 0.08 = `64 for the second year; (`800 – `200) × 0.08 = `48 for the third year, (`600 – `200) × 0.08 = `32 for the fourth year and (`400 – `200) × 0.08 = `16 for the fifth year. The outstanding amount of bond would be zero at the end of fifth year.
Since the government will have to return `200 every year, the outflows every year will consist of interest payment and repayment of principal: `200 + `80 = `280; `200 + `64 = `264; `200 + `48 = `248;

The formula for determining the value of a bond or debenture that is amortized every year can be written as follows:
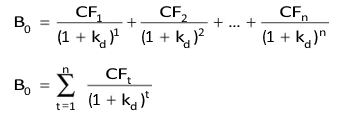
Note that cash flow, CF, includes both the interest and repayment of the principal.
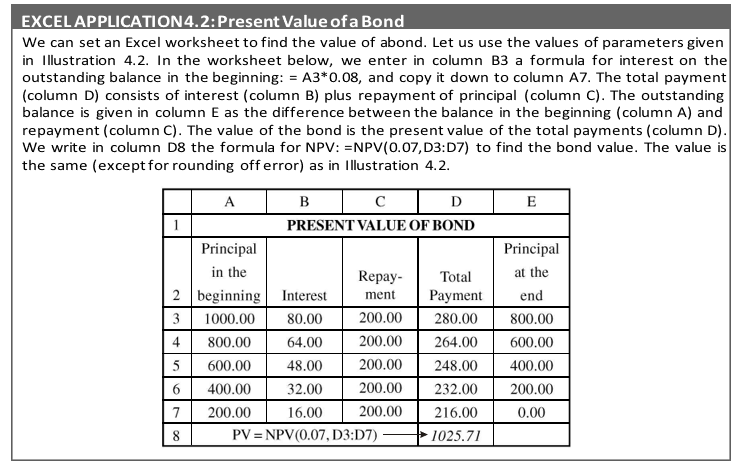
EXCEL APPLICATION 4.2: Present Value of a Bond
Bond Values and Semi-annual Interest Payments
It is a practice of many companies in India to pay interest on bonds (or debentures) semiannually. The formula for bond valuation can be modified in terms of half-yearly interest payments and compounding periods as given below:
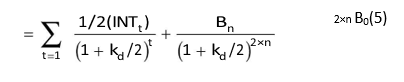

Pure Discount Bonds
Pure discount bonds do not carry an explicit rate of interest. They provide for the payment of a lump sum amount at a future date in exchange for the current price of the bonds. The difference between the face value of the bond and its purchase price gives the return or YTM to the investor. For example, a company may issue a pure discount bond of `1,000 face value for `520 today for a period of five years. Thus, the debenture has (a) purchase price of `520, (b) maturity value (equal to the face value) of `1,000 and (c) maturity period of five years. The rate of interest can be calculated as follows:
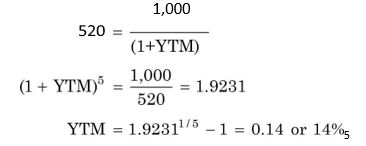
You can also use the trial and error method to obtain YTM, which is 14 per cent.
Pure discount bonds are also called deep-discount bonds or zero-interest bonds or zero coupon bonds. Industrial Development Bank of India (IDBI)* was the first to issue a deep discount bond in India in January 1992. The bond of a face value of `1,00,000 was sold for `2,700 with a maturity period of 25 years. If an investor held the IDBI deep-discount bond for 25 years, she would earn an implicit interest rate of: 2,700 = 1,00,000/(1 + i)25 = 15.54 per cent. IDBI again issued a deep-discount bond in 1998 at a price of `12,750, to be redeemed
after 30 years at the face value of `5,00,000. The implicit interest rate for this bond works out to be 13 per cent.
It is quite simple to find the value of a pure discount bond as it involves one single payment (face value) at maturity. The market interest rate, also called the market yield, kd, is used as the discount rate. The present value of this amount is the bond value. Value of a pure discount bond = PV of the amount on maturity:
Consider the IDBI bond with a face value of `5,00,000 with a maturity of 30 years. Suppose the current market yield on similar bonds is 9 per cent. The value of the IDBI pure-discount bond today is as follows:
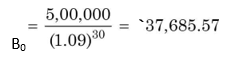
Perpetual Bonds (Irredeemable Bonds)
Suppose that a 10 per cent, `1,000 bond will pay `100 annual interest into perpetuity? What would be its value of the bond if the market yield or interest rate were 15 per cent? The value of the bond is determined as follows:
Perpetual bonds, also called consols, have an indefinite life and therefore, have no maturity value. Perpetual bonds or debentures are rarely found in practice. After the Napoleanic War, England issued these types of bonds to pay off many smaller issues that had been floated in prior years to pay for the war.2 In case of the perpetual bonds, as there is no maturity, or terminal value, the value of the bonds would simply be the discounted value of the infinite stream of interest flows.
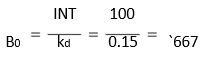
If the market yield is 10 per cent, the value of the bond will be `1,000 and if it is 20 per cent the value will be `500. Thus the value of the bond will decrease as the interest rate increases and vice-versa. Table 4.1 gives the value of a perpetual bond paying annual interest of `100 at different discount (market interest) rates.
Table 4.1: Value of a Perpetual Bond at Different Bond at Different Discount Rates

VALUATION OF PREFERENCE SHARES
A company may issue two types of shares: (a) ordinary shares and (b) preference shares. Ordinary shares are known as common shares in USA. Owners of shares are called shareholders, and capital contributed by them is called share capital. Ordinary shareholders are also called equity shareholders.
Preference shares have preference over ordinary shares in terms of payment of dividend and repayment of capital if the company is wound up. They may be issued with or without a maturity period. Redeemable preference shares are shares with maturity. Irredeemable preference shares are shares without any maturity.* The holders of preference shares get dividends at a fixed rate. With regard to dividends, preference shares may be issued with or without cumulative features. In the case of cumulative preference shares unpaid dividends accumulate and are payable in the future. Dividends in arrears do not accumulate in the case of non-cumulative preference shares.
Preference Shares vs Ordinary Shares
The following are the features of preference and ordinary shares:
ConversionA company can issue convertible preference shares. That is, after a stated period, such shares can be converted into ordinary shares.
Claims Preference shareholders have a claim on assets and incomes prior to ordinary shareholders. Equity (ordinary) shareholders have a residual claim on a company’s incomes and assets. The equity shareholders are the legal owners of the company. Dividend. The dividend rate is fixed in the case of preference shares. Preference shares may be issued with cumulative rights, i.e., dividend will accumulate until paid-off. In the case of equity shares, neither the dividend rate is known, nor does dividend accumulate. Dividends paid on preference and equity shares are not tax deductible. In India, if a company pays dividend, it has to pay dividend distribution tax. RedemptionRedeemable preference shares have a maturity date. Equity shares have no maturity date.
Like bonds, it is relatively easy to estimate cash flows associated with preference shares. The cash flows may include annual preference dividend and redemption value on maturity in case of redeemable preference shares. The value of the preference share would be the sum of the present values of dividends and the redemption value.
ILLUSTRATION 4.4: Value of a Preference Share
Suppose an investor is considering the purchase of a 12-year, 10 per cent `100 par value preference share. The redemption value of the preference share on maturity is `120. The investor’s required rate of return is 10.5 per cent. What should she be willing to pay for the share now?
The investor would expect to receive `10 as preference dividend each year for 12 years and `120 on maturity (i.e., at the end of 12 years). We can use the present value annuity factor to value the constant stream of preference dividends and the present value factor to value the redemption payment.
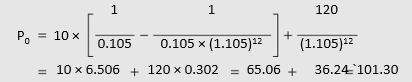
Note that the present value of `101.30 is composite of the present value of dividends, `65.06 and the present value of the redemption value, `36.24. The `100 preference share is worth `101.3 today at 10.5 per cent required rate of return. The investor would be better off by purchasing the share for `100 today.
A formula similar to the valuation of bonds can be used to value preference shares with a maturity period:

PDIVt is the preference dividend per share in period t, kp the required rate of return of preference share and Pn the value of the preference share on maturity. Since PDIV is an annuity, Equation (8) can also be written as follows:
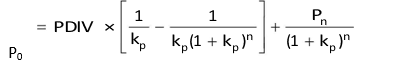
Note that the term within parentheses on the right-hand side of the equation is the present value factor for an annuity of `1.
Valuing Irredeemable Preference Share
Assume if irredeenable preference shares were allowed. How can we value an irredeemable preference share? Consider that a company has issued `100 irredeemable preference shares on which it pays a dividend of `9. Assume that this type of preference share is currently yielding a dividend of 11 per cent. What is the value of the preference share? The preference dividend of `9 is a perpetuity. Therefore, the present value of the preference share is:
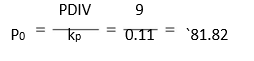
Yield on Preference Share
We can ask a different question. If the price of the irredeemable preference share is `81.82, what return do investors require? In that case, we will have to solve the following equation
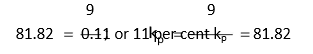
VALUATION OF ORDINARY SHARES
The valuation of ordinary or equity shares is relatively more difficult. The difficulty arises because of two factors:5 First, the rate of dividend on equity shares is not known; also, the payment of equity dividend is discretionary, i.e., dependent on the company’s discretion. Thus, the estimates of the amount and timing of the cash flows expected by equity shareholders are more uncertain. In the case of debentures and preference shares, the rate of interest and dividend, respectively, are known with certainty. It is, therefore, easy to make the forecasts of cash flows associated with them. Second, the earnings and dividends on equity shares are generally expected to grow, unlike the interest on bonds and preference dividend. This feature of variable dividend on equity shares makes the calculation of share value difficult.
Dividend Capitalization
The general principle of valuation applies to the share valuation. The value of a share today depends on cash inflows expected by investors and the risks associated with those cash inflows. Cash inflows expected from an equity share consist of dividends that the owner expects to receive while holding the share and the price, which he expects to obtain when the share is sold. The price, which the owner is expected to receive when he sells the share, will include the original investment plus a capital gain (or minus a capital loss).
Single Period Valuation
Normally a shareholder does not hold shares in perpetuity. He holds shares for some time, receives the dividends and finally, sells them to a buyer to obtain capital gains. But when he sells the share, the new buyer is also simply purchasing a stream of future dividends and a liquidating price when he in turn sells the share. The logic can be extended further. The ultimate conclusion is that, for shareholders in general, the expected cash inflows consist only of future dividends and, therefore, the value of an ordinary share is determined by capitalising the future dividend stream at the opportunity cost of capital. The opportunity cost of capital is the return that the shareholder could earn from an investment of equivalent risk in the market. The value of a share is the present value of its future stream of dividends. How can a share be valued?
Let us assume that an investor intends to buy a share and will hold it for one year. Suppose he expects the share to pay a dividend of `2 next year, and would sell the share at an expected price of `21 at the end of the year. If the investor’s opportunity cost of capital or the required rate of return (ke) is 15 per cent, how much should he pay for the share today?
The present value of the share today, P0, will be determined as the present value of the expected dividend per share at the end of the first year, DIV1, plus the present value of the expected price of the share, after a year, P1.
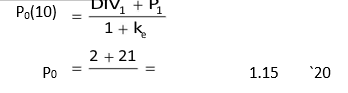
Equation (10) gives the ‘fair’ or ‘reasonable’ price of the share since it reflects the present value of the share. The investor would buy the share if the actual price were less than `20. In a well-functioning capital market, there ought not to be any difference between the present value and market value of the share. Investors would have full information and it would be reflected in the market price of the share in a well-functioning market. In practice, there could be a difference between the present value and the market value of a share due to imperfections in the capital markets. An under-valued share has a market price less than the share’s present value. On the other hand, an over-valued share has a market price higher than the share’s present value.
It may be seen in the example that the share value after a year represents an expected growth (g) or capital gain of 5 per cent:
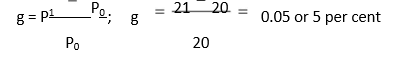
An investor can, thus, represent his expectation with regard to the future share price in terms of expected growth. If the share price is expected to grow at g per cent, then we can write P1 as follows:

In other words, the present value of a share is determined by its expected dividend, discounted by the difference of the shareholder’s capitalization, or required, rate of return (ke) and growth rate (g). In the example, if the investor would have expected the share price to grow at 5 per cent, the value of the share today using Equation (12) will be:
2 2
P0 0.15 0.05 0.10 `20
Multi-period Valuation
In the preceding section, we discussed a single-period share valuation model, where the investor was expected to hold the share for one year and then sell it at the end of the year. The investor will receive dividend for one year, DIV1, and the share value, P1, when he sells the share at the end of the year. The value of the share today is given by Equation (10).
Multi-period Valuation
In the preceding section, we discussed a single-period share valuation model, where the investor was expected to hold the share for one year and then sell it at the end of the year. The investor will receive dividend for one year, DIV1, and the share value, P1, when he sells the share at the end of the year. The value of the share today is given by Equation (10).
Why does the new investor purchase the share at the end of one year? Because he also expects a stream of dividends during the period he holds the share plus the liquidating price of the share. What determines the next year’s price (P1) if the share is held for one year? The price next year (P1) will depend on expected dividend in year 2 and expected price of the share at the end of year 2. For example, if we consider that DIV2 = `2.10 and P2 = `22.05, then P1 is:
2.10 22.05
P1 – 1.15 `21
Today’s price (P0) can be calculated as the discounted value of dividends in years 1 and 2 and liquidating price at the end of year 2 as follows:
2 2.10 22.05
P0 – 1.15 (1.15)2 = `20
Thus, if Equation (10) holds, P1 should be given by the following formula:
P1 – DIV1 2 keP2
We can express P0 as follows:
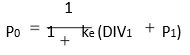
By substituting the value of P1 from Equation (13), we obtain the share price today as given below:
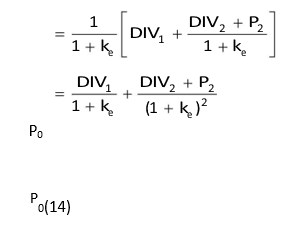
We can further extend the time horizon. We can, for example, determine the price of the share after 2 years (P2):
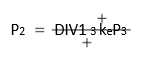
and determine today’s price, P0, in terms of dividends for 3 years and price after 3 years. If the final period is n, we can write the general formula for share value as follows:
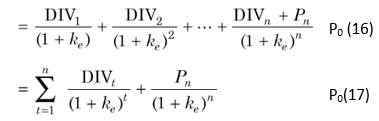
How does Equation (17) work? Consider an example, as given in Illustration 4.5.
ILLUSTRATION 4.5: Value of a Share Under Constant Growth
Suppose the price of a share today (P0) is `20 and it is expected to increase at an annual rate of 5 per cent. Thus, the price after a year will be: `20 (1.05) = `21; after two years: `21 (1.05) = `22.05 and so on. Further, assume that the expected dividend after a year (DIV1) is `2, and it is also expected to grow at a rate of 5 per cent per annum. Thus, the expected dividend after two years will be: `2 (1.05) = `2.10; after three years: `2.10 (1.05) = `2.21 and so on. Suppose the opportunity cost of capital is 15 per cent, what would be the price of share if it were held for 5 years?
The price would equal the present value of dividends for 5 years plus the present value of the share price at the end of 5 years. That is:
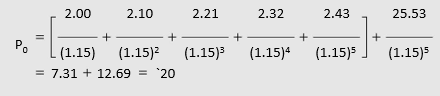
The present value of the stream of dividends is `7.31 and of the share price at the and of five years is `12.69. The total present value of the share is `20.
We use the values in Illustration 4.5 to show the present values of dividend stream [PV (DIVt)] and the future price [PV (Pn)] separately in Table 4.2. You can see from Table 4.2 and Figure 4.1 that as the time horizon lengthens, the proportion of present value contributed by the dividends increases. The present value of future (terminal or liquidating) price declines as the time horizon increases; it is almost zero for 50-year or higher time horizon. You may also notice that after about 50 years the present value contribution of additional dividends
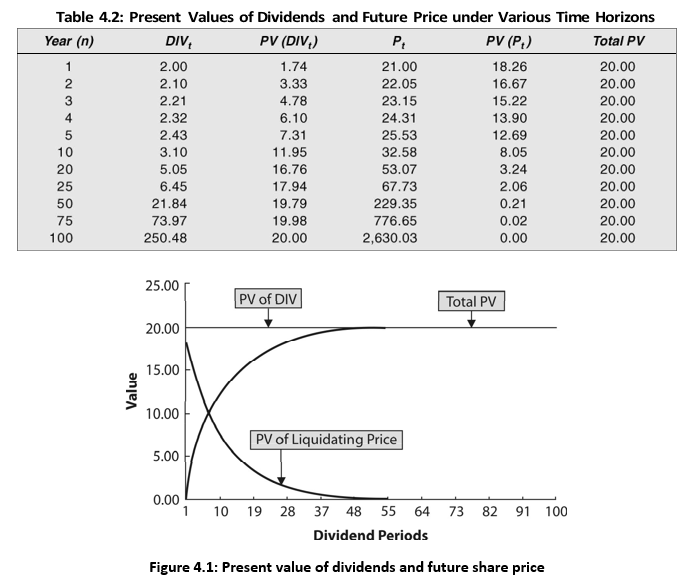
is insignificant. The total present value of dividends plus terminal price remains the same, i.e., `20, irrespective of the time horizon.4
n could be very large; in fact, it can be assumed to approach
infinity ( ). If the time horizon, n, approaches to infinity, then the present value of the future price will approach to zero. Thus the price of a share today is the present value of an infinite stream of dividends
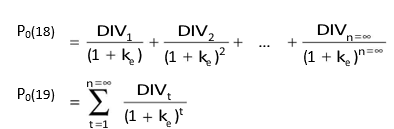
It will be observed that the procedure for calculating the share value is similar to the calculation of an asset’s present value; cash flows in terms of dividend stream are discounted by the opportunity cost of capital or the capitalization rate. It must be remembered that the formula for determining the share price, i.e., Equation (18) or Equation (19), does not ignore terminal value of the share and capital gains. The basis of formula was the assumption that value is determined by expected dividends and the terminal price, Pn.5 The term representing the terminal price has disappeared from the formula because, as we have shown in Table 4.2 and Figure 4.1, as the holding period approaches infinity, the present value of the terminal price approaches zero.
Dividends, DIVt, in Equation (17 or 19) represent stream of expected dividends. In practice, DIVt could rise, fall, remain constant, or fluctuate randomly. In the following sections, we discuss the cases of rising, falling and constant dividends.
Growth in Dividends
Dividends do not remain constant. Earnings and dividends of most companies grow over time, at least, because of their retention policies. Historical evidence indicates that most companies have been retaining a substantial portion of their earnings (about 50 per cent) for reinvestment in the business. This policy would increase the ordinary shareholder’s equity as well as the firm’s future earnings. If the number of shares does not change, this policy should tend to increase the earnings per share, and consequently, it should produce an expanding stream of dividends per share.
Normal Growth
If a totally equity financed firm retains a constant proportion of its annual earnings (say, b) and reinvests it at its internal rate of return, which is its return on equity (ROE) without any external funds, then it can be shown that the dividends will grow at a constant rate equal to the product of retention ratio and return on equity; that is, g = b × ROE. To illustrate how dividends grow over time, consider a numerical example.
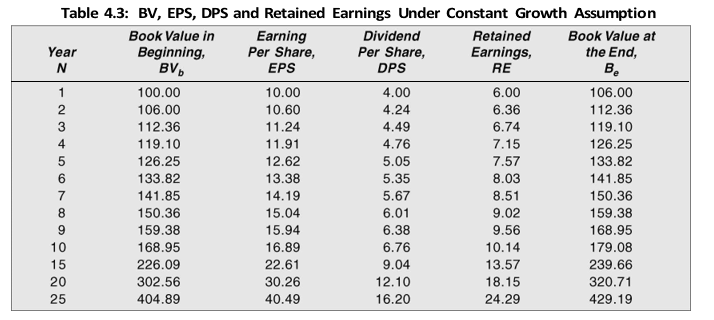
Suppose the book value of a firm’s equity per share today is `100, and its return on equity (ROE) is 10 per cent. The firm’s retention ratio is 60 per cent (which implies a payout ratio of 40 per cent). It is expected that the firm will also earn 10 per cent on its retained earnings. Let us also assume that the firm has no debt. The firm’s earnings per share after one year will be: EPS1 = `100 × 0.10 = `10. The firm will retain `6 and distribute `4 as dividends. The book value of equity per share at the end of the first year will be: BV1 = `100 + `6 = `106. The firm’s EPS in second year will be: EPS2 = `106 × 0.10 = `10.6. Again, it will retain 60 per cent of the earnings, viz., `6.36 and distribute 40 per cent, viz., `4.24. The growth in dividend per share will be:

You can verify that EPS has also grown at the rate of 6 per cent. It may be noticed that the increase in dividend per share by `0.36 in the second year has occurred on account of the reinvestment of earnings. The firm had retained `6 per share out of the first year’s earnings of `10 per share, and earned additional earnings of `0.60 per share at the rate of 10 per cent. The 40 per cent of the additional income has also gone as dividend to the shareholders in the second year. The example can be extended to verify that dividends in subsequent years will continue growing at a constant rate of 6 per cent.
Table 4.3 shows the growth in book value, earnings per share, dividend per share and retained earnings over a given period of time. It should be noted that 6 per cent growth in dividends is equal to the product of retention rate of 60 per cent and return on equity of 10 per cent: 0.60 × 0.10 = 0.06 or 6 per cent:
Growth = Retention ratio × Return on equity
g = b × ROE
It can be seen that growth will be more if the firm retains higher portion of earnings. The current dividend will, however, be reduced. A share valuation model should explicitly involve growth expectations. Let us assume that dividends grow at a constant rate to infinity. If the firm now pays dividend DIV0 (that is, dividend in year, 0), then dividend at the end of first year will be:
DIV = DIV (1+ )1 0 g 1
and at the end of the second year, it will be:


In words, the present value of a share is equal to the dividend after a year, DIV1, divided by the difference of the capitalization rate (ke) and the growth rate (g); that is, (ke – g). Equation (23) is the perpetual growth model. It is based on the following assumptions:6
The capitalization rate or the opportunity cost of capital must be greater than the growth rate, (ke > g), otherwise absurd results will be attained. If ke = g, the equation will yield an infinite price, and if ke < g, the result will be a negative price. The initial dividend per share, DIV1, must be greater than zero (i.e., DIV1 > 0), otherwise Equation (23) will obtain a zero price.
The relationship between ke and g is assumed to remain constant and perpetual.

Super-normal Growth
The dividends of a company may not grow at the same constant rate indefinitely. It may face a two-stage growth situation. In the first stage, dividends may grow at a super-normal growth
ratewhen the company is experiencing very high demand for its products and is able to extract premium from customers. Afterwards, the demand for the company’s products may normalize and therefore, earnings and dividends may grow at a normal growthrate. The share value in a two-stage growth situation can be determined in two parts. First, we can find the present value of constantly growing dividend annuity for a definite super-normal growth period. Second, we can calculate the present value of constantly growing dividend, indefinitely (in perpetuity), after the super-normal growth period. Let us consider an example in Illustration 4.8.
Thus, it is clear that the value of the share is equal to the discounted value of dividends for the first six years, growing at an above-average or super-normal growth rate of 15 per cent, plus the discounted value of dividends indefinitely after six years, growing at the normal rate of 8 per cent.
We find from Illustration 4.8 that the basic valuation methodology remains the same in two-stage growth situation. The perpetual growth model, as given in Equation (23), should be appropriately modified. By expanding Equation (23) one could incorporate various growth


periods in the analysis. If the dividends of a firm are expected to grow at a super normal growth rate, gs, for n years and then grow at a normal growth rate, gn, till infinity, the value of the share is given as follows:
super-normal growth period
+ PV of dividends during indefinite normal growth period
| EXCEL APPLICATION 4.3: Two-Stage Growth |
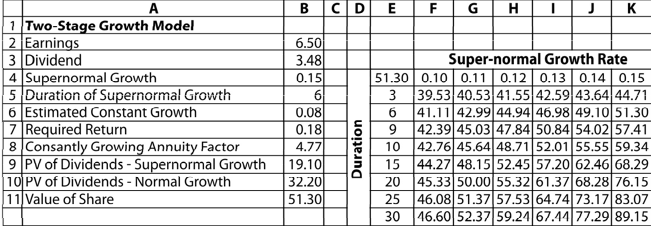
We can solve the two-stage growth model in Excel. The following is the worksheet based on the data given in Illustration 4.8. For the first 6 years, the dividend grows at a constant rate of 15 per cent per annum. Given 15 per cent growth rate, 18 per cent required rate of return and the time duration of 6 years, in column B8 of the worksheet we enter the formula for a constantly growing annuity:
= (1/(B7–B4))*(1–((1+B4)/(1+B7))^B5)
To obtain the present value of the dividends over six years, in column B9 we write the formula: = B3*(1+B4)*B8. In this formula the dividend in the first year is given by: DIV1 = B3*(1+B4). After 6 years, the dividend grows at 8 per cent indefinitely. The value of these dividends is given by: V0 = [DIV7/(0.18 – 0.15)] × (1/(1.18)6. We enter a formula in B10: = ((B3*(1+B6)^B5)*(1+B6))/(B7-B4))*(1/ (1+B7)). The formula in B11: =B9+B10 gives the total value of the share.
Using Excel, we create a two-variable table that explains the sensitivity of the share value with regard to changes in the super-normal growth rate (in row) and its duration (in column). The longer the super-normal growth rate is, the higher the value of the share will be.
You may use the following steps to calculate the value of a share growing at the supernormal rate for some period and then at the normal rate forever:7
Calculate dividend per share for the super-normal growth period and use the common procedure for calculating the present value of the stream of dividends for the supernormal growth period.
Calculate the present value of the share at the end of the supernormal growth period (Pn) as shown below:
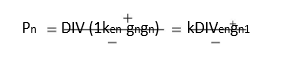
Calculate the present value of Pn at t = 0. That is
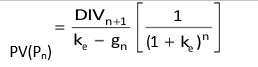
Calculate the total value of the share by adding values arrived in the first and third steps.
What would be the price of the share in Illustration 4.8 if (a) growth in dividends is zero and (b) growth in dividends is 8 per cent per annum forever? If g = 0, then P0 will be:

It may be noticed from the preceding illustrations that as one moves from zero-growth assumption to supernormal-growth assumption, the price of the share increases from `19.33 to `37.30. Thus, the price of a share increases with growth in earnings and dividends, other things remaining the same.
Firm Paying no Dividends
It sometimes so happens that a company although earns profits but does not declare dividends. How would the dividend-capitalization model explain the share value under such circumstances? However, companies paying no dividends do command positive market prices for their shares since the price today depends on the future expectation of dividends. The non-payment of dividends may not last forever. Eventually, these companies may start paying dividends one day. Shareholders hold shares of such companies because they expect that in the final analysis dividends will be paid, or they will be able to realize capital gains. Thus, the dividend capitalization model is a valid share valuation model even for those companies that are presently paying no dividends.
Suppose a company is expected to pay a dividend of `2 per share on its shares from fifth year to infinity. In present value terms, the share is worth the present value of dividends from year five to infinity, discounted at the opportunity cost of capital. For example, at a required rate of return of 20 per cent, a perpetual sum of `2 starting from fifth year, is worth `10 at the end of fourth year:
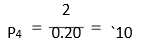
The `10 may be considered as a lump sum received at the end of fourth year. The worth of the share today will be the discounted value of `10:
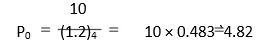
Alternatively, we assume that `2 flows in from the very beginning, and thus, calculate the worth of the share today as: `10 (P0 = `2/0.20). But we know that the firm will not pay any dividend for the first four years. If we subtract the present value of dividends not received from the calculated price of `10, we obtain the actual present worth of the share; this would again be `4.82; that is, `10 – (`2 × 2.589) = `4.82. (Note that the factor, 2.589, is the present value annuity factor for four years at 20 per cent rate). This procedure can be adopted to incorporate growth in dividends.
Earnings Capitalization
The dividend capitalization model, discussed so far, is the basic share valuation model. However, under two cases, the value of the share can be determined by capitalizing the expected earnings:8 When the firm pays out 100 per cent dividends, that is, it does not retain any earnings. When the firm’s return on equity (ROE) is equal to its opportunity cost of capital (ke). The first case in which the earnings capitalization model may be employed is the one when the earnings of the firm are stable. The earnings will not grow if the firm does not retain the earnings (and also does not employ any debt). Thus, if the retention rate, b, is zero, then the growth rate, g, would also be equal to zero and DIV1 would be equal to EPS1. Under these conditions, the value of the share will be equal to the expected earnings per share divided by the equity capitalization rate. Since DIV1 = EPS1 (1 – b) and g = rb (where r is assumed to be equal to ROE), we can write formula for share valuation as follows:

The second situation, in which the earnings capitalization will yield the same result as the dividend capitalization, is when the firm lacks real growth opportunities. That is, it earns a rate equal to its cost on its retained earnings. If r = ke, then g = rb = keb. Substituting the value of g in Equation (26), we obtain:
![]()
Thus, true growth, as opposed to mere expansion, is dependent on the existence of growth opportunities, to reinvest retained earnings at a rate higher than the capitalization rate, ke, thereby creating net present value over and above the investment outlays required.9
ILLUSTRATION 4.10: Earnings Model
Calculate the price of a share if EPS = `2.50, b = 0.4, ke = 0.10 and ROE = r = 0.20. What shall be the price if r = ke = 0.10?
Employing Equation (26) the price of share, when r = 0.20 will be

However, if r = ke, the price can be determined simply as P0 = EPS1/ke. In this illustration using this formula we shall have the same answer as above.
Caution in Using Constant-growth Formula
The constant growth formula is a useful rule of thumb for calculating the present value of a share and the opportunity cost of capital (or the capitalization rate)11. A blind faith in the formula can be misleading. One should be cautious in using the formula for the following:
Estimation errors: It is dangerous to estimate the capitalization rate, ke, by analysing just one share. A large sample of equivalent risk shares should be employed to estimate ke. This procedure would help at least to reduce the extent of estimating errors.
Unsustainable high current growth: The formula should not be used for those companies which have high current growth rates. The constant-growth formula unrealistically assumes that such growth rates can be sustained indefinitely. Since growth rates slow down with the maturity of firms, the assumption tends to overestimate ke. It is not realistic to assume that a firm will continue growing forever at 50 per cent, or even 25 per cent.
Errors in forecasting dividends: The market’s estimate of the value of a share may be different from the estimate derived from the constant-growth formula. That does not mean that the formula is incorrect; the reason probably may be that dividend stream has not been correctly forecasted.
Check Your Concepts
- What is meant by dividend capitalization?
- How are ordinary shares valued under no-growth situation?
- What is dividend-growth model of share valuation? Why is it called perpetual-growth model?
- What is super-normal growth? How is a share valued when its dividends grow in two stages—first at super-normal growth and later at normal growth rate?
- Under what conditions can we use earnings capitalization approach for share valuation?
- What cautions should be taken in using the constant-growth model of share valuation?
EQUITY CAPITALIZATION RATE
Suppose the current market price of BHEL’s share is `240 and the current dividend per share is `12. You expect dividend per share to grow at 10 per cent per annum forever. How much return do you require for investing in the share? We assume that the current price of BHEL’s share is a fair price. The expected dividend per share next year, DIV1, is `13.20 (12 × 1.10). The expected dividend yield is 5.5 per cent (13.20/240) and the expected growth rate is 10 per cent. Therefore, your minimum required rate of return is 15.5 per cent. If you earn less than 15.5 per cent, the current share price cannot be maintained.
So far we have discussed how the present value of a share can be calculated. One must know the expected dividends and the required rate of return (the opportunity cost of capital or capitalization rate). The required rate of return will depend upon the risk of the share. Hence, the required rate of return will be equal to the risk-free rate of interest plus the riskpremium to account for the share’s risk. The risk premium would be different for different shares because of the difference in their risk. We shall discuss this method of calculating the required rate of return on equity in a chapter later on.
In a well-functioning capital market, the market price is the fair price of a share. Therefore, the shareholders expect the share to earn a minimum return that keeps the current share price intact. For firms for which dividends are expected to grow at a constant rate indefinitely and the current market price is given, we can modify and use Equation (23) to estimate the capitalization or the required rate of return of the share:
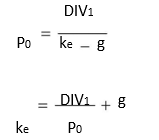
ILLUSTRATION 4.11: Equity Capitalization Rate
A company’s share is currently selling for `50 per share. It is expected that a dividend of `3 per share will be paid after one year, which will grow at 8 per cent indefinitely. What is the equity capitalization rate? The equity capitalization rate is given as follows:
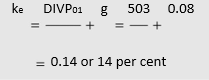
SUMMARY
In this chapter we have applied the concept of present value to explain the value of bonds and shares. Like any other assets, the present value of a bond or a share is equal to the discounted value of the stream of cash flows—the discount rate being the rate of return that investors expect from securities of comparable risk.
Bonds or debentures are debt instruments or securities. In case of a bond/debenture the stream of cash flows consists of annual interest payments and repayment of principal. These flows are fixed and known. The value of the bond can be found by capitalizing these flows at a rate of return, which reflects their risk. The market interest
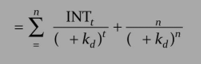
rate or yield is used as the discount rate in case of bonds (or debentures). The basic formula for the bond value is as follows:
B
B0
t 1 1 1
When the price of a bond is given, a bond’s yield to maturity or internal rate of return can be found by equating the present value of the bond’s cash outflows with its price.
Zerointerest bonds (called zerocoupon bonds in USA) do not have explicit rate of interest. They are issued for a discounted price; their issue price is much less than the face value. Therefore, they are also called deepdiscount bonds. The basic discounting principles apply in determining the value or yield of these bonds.
Preference shares have a preference over ordinary shareholders with regard to dividends. The preference dividend is specified and known. Preference share value can be determined in the same way as the bond value.
Cash flows of an ordinary (or equity) share consist of the stream of dividends and terminal price of the share. Unlike the case of a bond, cash flows of a share are not known. Thus, the risk of holding a share is higher than the risk of a bond. Consequently, equity capitalization rate will be higher than that of a bond. The general formula for the share valuation is as follows:
P0 1 1 1 1 2 1 1 n
As the time horizon, n, becomes very large (say, extends to infinity) the present value of future price approaches zero. Thus the term Pn disappears from the formula, and we can use the following equation to find the value of a share today:
P0 1 1 t t 1

Review Questions
- Explain the concept of valuation of securities? Why is the valuation concept relevant for financialdecision-making purposes?
- What is a bond? Is it same as a debenture? What are the features of a bond?
- Illustrate the method of valuing (i) bonds in perpetuity and (ii) bonds with maturity.
- What is the difference between the valuation of a bond and of a preference share? Illustrate.
- What is the meaning of the term yield-to-maturity for bonds and preference shares? Is it appropriateto talk of a yield-to-maturity on a preference share that has no specific maturity date?
- What is an ordinary share? What are its features? How does it differ from a preference share anda debenture?
- Explain in detail the method of valuing an ordinary share.
- What is the perpetual growth model? What are its assumptions? Is this model applicable in afinite case?
- Why are dividends important in determining the present value of a share? How would you accountfor the positive market value of a company’s share, which currently pays no dividend?
- How will you value a share which grows at an abnormal rate for a finite period followed by normalgrowth in perpetuity? Illustrate your answer with an example.
- What are the conditions for using earning-capitalization model for valuing a share?
