RISK AND UNCERTAINTY
Risk involves situations or events which may or may not occur, but whose probability of occurrence can be calculated statistically and the frequency of their occurrence predicted from past records. Thus insurance deals with risk.
Uncertain events are those whose outcome cannot be predicted with statistical confidence.
In everyday usage the terms risk and uncertainty are not clearly distinguished. If you are asked for a definition, do not make the mistake of believing that the latter is a more extreme version of the former. It is not a question of degree, it is a question of whether or not sufficient information is available to allow the lack of certainty to be quantified. As a rule, however, the terms are used interchangeably.
Risk preference
People may be risk seekers, risk neutral or risk averse.
A risk seeker is a decision maker who is interested in the best outcomes no matter how small the chance that they may occur.
A decision maker is risk neutral if he is concerned with what will be the most likely outcome.
A risk averse decision maker acts on the assumption that the worst outcome might occur.
This has clear implications for managers and organisations. A risk seeking manager working for an organisation that is characteristically risk averse is likely to make decisions that are not congruent with the goals of the organisation. There may be a role for the management accountant here, who could be instructed to present decision-making information in such a way as to ensure that the manager considers all the possibilities, including the worst.
ALLOWING FOR UNCERTAINTY
Management accounting directs its attention towards the future and the future is uncertain. For this reason a number of methods of taking uncertainty into consideration have evolved.
Research techniques to reduce uncertainty
Market research can be used to reduce uncertainty.
Market research is the systematic process of gathering, analysing and reporting data about markets to investigate, describe, measure, understand or explain a situation or problem facing a company or organisation.
Market research involves tackling problems. The assumption is that these problems can be solved, no matter how complex the issues are, if the researcher follows a line of enquiry in a systematic way, without losing sight of the main objectives. Gathering and analysing all the facts will ultimately lead to better decision making.
The role of market research
In the last 20 years or so market research has become a much more widespread activity. Organisations – in the private sector, the public sector and the not-for-profit sector – rely on research to inform and improve their planning and decision making.
Market research enables organisations to understand the needs and opinions of their customers and other stakeholders. Armed with this knowledge they are able to make better quality decisions and provide better products and better services.
Thus, research influences what is provided and the way it is provided. It reduces uncertainty and monitors performance. A management team which possesses accurate information relating to the marketplace will be in a strong position to make the best decisions in an increasingly competitive world.
Decision-makers need data to reduce uncertainty and risk when planning for the future and to monitor business performance. Market researchers provide the data that helps them to do this.
Types of data collected
Data can be either primary (collected at first hand from a sample of respondents), or secondary (collected from previous surveys, other published facts and opinions, or from experts). Secondary research is also known as desk research, because it can be carried out from one’s desk.
More importantly for research practice and analysis, data can be either quantitative or qualitative.
Quantitative data usually deals with numbers and typically provides the decision maker with information about how many customers, competitors etc act in a certain way. Quantitative data can, for example, tell the researcher what people need or consume, or where, when and how people buy goods or consumer services.
Qualitative data tells us why consumers think/buy or act the way they do. Qualitative data is used in consumer insight (eg understanding what makes consumers prefer one brand to another), media awareness (eg how much of an advertisement is noticed by the public), new product development studies and for many other reasons.
Qualitative research has as its specific purpose the uncovering and understanding of thought and opinion. It is carried out on relatively small samples and unstructured or semi-structured techniques, such as individual in depth interviews and group discussions (also known as focus groups), are used.
Conservatism
This approach simply involves estimating outcomes in a conservative manner in order to provide a built-in safety factor.
However, the method fails to consider explicitly a range of outcomes and, by concentrating only on conservative figures, may also fail to consider the expected or most likely outcomes.
Conservatism is associated with risk aversion and prudence (in the general sense of the word). In spite of its shortcomings it is probably the most widely used method in practice.
Worst/most likely/best outcome estimates
A more scientific version of conservatism is to measure the most likely outcome from a decision, and the worst and best possible outcomes. This will show the full range of possible outcomes from a decision, and might help managers to reject certain alternatives because the worst possible outcome might involve an unacceptable amount of loss. This requires the preparation of pay-off tables.
Pay-off tables
Pay-off tables identify and record all possible outcomes (or pay-offs) in situations where the action taken affects the outcomes.
PROBABILITIES AND EXPECTED VALUES
Expected values indicate what an outcome is likely to be in the long term with repetition. Fortunately, many business transactions do occur over and over again.
Although the outcome of a decision may not be certain, there is some likelihood that probabilities could be assigned to the various possible outcomes from an analysis of previous experience.
Expected values
Where probabilities are assigned to different outcomes we can evaluate the worth of a decision as the expected value, or weighted average, of these outcomes. The principle is that when there are a number of alternative decisions, each with a range of possible outcomes, the optimum decision will be the one which gives the highest expected value.
Limitations of expected values
The preference for B over A on the basis of expected value is marred by the fact that A’s worst possible outcome is a profit of RWF5,000, whereas B might incur a loss of RWF2,000 (although there is a 70% chance that profits would be RWF7,000 or more, which would be more than the best profits from option A).
Since the decision must be made once only between A and B, the expected value of profit (which is merely a weighted average of all possible outcomes) has severe limitations as a decision rule by which to judge preference. The expected value will never actually occur.
Expected values are used to support a risk-neutral attitude. A risk-neutral decision maker will ignore any variability in the range of possible outcomes and be concerned only with the expected value of outcomes.
Expected values are more valuable as a guide to decision making where they refer to outcomes which will occur many times over. Examples would include the probability that so many customers per day will buy a can of baked beans, the probability that a customer services assistant will receive so many phone calls per hour, and so on.
DECISION RULES
The ‘play it safe’ basis for decision making is referred to as the maximin basis. This is short for ‘maximise the minimum achievable profit’.
A basis for making decisions by looking for the best outcome is known as the maximax basis, short for ‘maximise the maximum achievable profit’.
The ‘opportunity loss’ basis for decision making is known as minimax regret.
The maximin decision rule
The maximin decision rule suggests that a decision maker should select the alternative that offers the least unattractive worst outcome. This would mean choosing the alternative that maximises the minimum profits.
Suppose a businessman is trying to decide which of three mutually exclusive projects to undertake. Each of the projects could lead to varying net profit under three possible scenarios.
Minimax regret rule
The minimax regret rule aims to minimise the regret from making the wrong decision. Regret is the opportunity lost through making the wrong decision.
We first consider the extreme to which we might come to regret an action we had chosen.
Regret for any combination of action and circumstances = Profit for best action in those circumstances – Profit for the action actually chosen in those circumstances
The minimax regret decision rule is that the decision option selected should be the one which minimises the maximum potential regret for any of the possible outcomes
Contribution tables
Questions requiring application of the decision rules often incorporate a number of variables, each with a range of possible values. For example these variables might be:
− Unit price and associated level of demand
− Unit variable cost
Each variable might have, for example, three possible values.
Before being asked to use the decision rules, exam questions could ask you to work out contribution for each of the possible outcomes. (Alternatively profit figures could be required if you are given information about fixed costs.)
The number of possible outcomes = number of values of variable 1 x number of values of variable 2 x number of values of variable 3 etc
So, for example, if there are two variables, each with three possible values, there are 3 x 3 = 9 outcomes.
Perhaps the easiest way to see how to draw up contribution tables is to look at an example.
DECISION TREES
Decision trees are diagrams which illustrate the choices and possible outcomes of a decision.
Rollback analysis evaluates the EV of each decision option. You have to work from right to left and calculate Evs at each outcome point.
A probability problem such as ‘what is the probability of throwing a six with one throw of a dice? Is fairly straightforward and can be solved using the basic principles of probability.
More complex probability questions, although solvable using the basic principles, require a clear logical approach to ensure that all possible choices and outcomes of a decision are taken into consideration.
Decision trees are a useful means of interpreting such probability problems.
A decision tree is a pictorial method of showing a sequence of interrelated decisions and their expected outcomes. Decision trees can incorporate both the probabilities of, and values of, expected outcomes, and are used in decision-making
Exactly how does the use of a decision tree permit a clear and logical approach?
− All the possible choices that can be made are shown as branches on the tree.
− All the possible outcomes of each choice are shown as subsidiary branches on the tree.
Constructing a decision tree.
There are two stages in preparing a decision tree.
− Drawing the tree itself to show all the choices and outcomes
− Putting in the numbers (the probabilities, outcome values and EVs)
Every decision tree starts from a decision point with the decision options that are currently being considered.
- It helps to identify the decision point, and any subsequent decision points in the tree, with a symbol. Here, we shall use a square shape.
- There should be a line, or branch, for each option or alternative
It is conventional to draw decision trees from left to right ,and so a decision tree will start as follows.
If the outcome from any choice is certain, the branch of the decision tree for that alternative is complete.
If the outcome of a particular choice is uncertain, the various possible outcomes must be shown.
We show the various possible outcomes on a decision tree by inserting an outcome point on the branch of the tree. Each possible outcome is then shown as a subsidiary branch, coming out from the outcome point. The probability of each outcome occurring should be written on the branch of the tree which represents that outcome.
To distinguish decision points from outcome points, a circle will be used as the symbol for an outcome point.
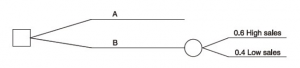
Evaluating the decision with a decision tree
Rollback analysis evaluates the V or each decision option. You have to work from right to left and calculate EVs at each outcome point.
The EV of each decision option can be evaluated, using the decision tree to help with keeping the logic on track. The basic rules are as follows.
We start on the right hand side of the tree and work back towards the left hand side and the current decision under consideration . This is sometimes known as the
‘rollback’ technique or ‘rollback analysis’
Working from right to left, we calculate the EV of revenue, cost contribution or profit at each outcome point on the tree
THE VALUE OF INFORMATION
Perfect information is guaranteed to predict the future with 100% accuracy. Imperfect information is better than no information at all but could be wrong in its prediction of the future.
The value of perfect information is the difference between the EV of profit with perfect information and the EV of profit without perfect information.
Perfect information removes all doubt and uncertainty from a decision, and enables managers to make decisions with complete confidence that they have selected the optimum course of action.
The value of perfect information.
Step 1
If we do not have perfect information and we must choose between two or more decision options we would select the decision option which offers the highest EV of profit. This option will not be the best decision under all circumstances. There will be some probability that what was really the best option will not have been selected, given the way actual events turn out.
Step 2
With perfect information, the best decision option will always be selected. The profits from the decision will depend on the future circumstances which are predicted by the information nevertheless, the EV of profit with perfect information should be higher than the EV of profit without the information.
Step 3
The value of perfect information is the difference between these two EVs
The value of imperfect information
There is one serious drawback to the technique we have just looked at: in practice, useful information is never perfect unless the person providing it is the sole source of the uncertainty. Market research findings or information from pilot tests and so on are likely to be reasonably accurate, but they can still be wrong: they provide imperfect information. It is possible, however, to arrive at an assessment of how much it would be worth paying for such imperfect information, given that we have a rough indication of how right or wrong it is likely to be.
. SENSITIVITY ANALYSIS
Sensitivity analysis can be used in any situation so long as the relationships between the key variables can be established. Typically this involves changing the value of a variable and seeing how the results are affected.
Approaches to sensitivity analysis
Sensitivity analysis is a term used to describe any technique whereby decision options are tested for their vulnerability to changes in any ‘variable’ such as expected sales volume, sales price per unit, material costs, or labour costs.
Here are three useful approaches to sensitivity analysis.
- To estimate by how much costs and revenues would need to differ from their estimated values before the decision would change.
- To estimate whether a decision would change if estimated costs were x% higher than estimated, or estimated revenues y% lower than estimated.
- To estimate by how much costs and/or revenues would need to differ from their estimated values before the decision maker would be indifferent between two options.
The essence of the approach, therefore, is to carry out the calculations with one set of values for the variables and then substitute other possible values for the variables to see how this affects the overall outcome.
- From your studies of information technology you may recognise this as what if analysis that can be carried out using a spreadsheet.
- From your studies of linear programming you may remember that sensitivity analysis can be carried out to determine over which ranges the various constraints have an impact on the optimum solution.
- Flexible budgeting can also be a form of sensitivity analysis.
SIMULATION MODELS
Simulation models can be used to deal with decision problems involving a number of uncertain variables. Random numbers are used to assign values to the variables.
One of the chief problems encountered in decision making is the uncertainty of the future. Where only a few factors are involved, probability analysis and expected value calculations can be used to find the most likely outcome of a decision. Often, however, in real life, there are so many uncertain variables that this approach does not give a true impression of possible variations in outcome.
To get an idea of what will happen in real life one possibility is to use a simulation model in which the values and the variables are selected at random. Obviously this is a situation ideally suited to a computer (large volume of data, random number generation).
The term ‘simulation’ model is often used more specifically to refer to modelling which makes use of random numbers. This is the ‘Monte Carlo’ method of simulation. In the business environment it can, for example, be used to examine inventory, queuing, scheduling and forecasting problems.
Uses of simulation
In the supermarket example above, the supermarket would use the information to minimise inventory holding without risking running out of the product. This will reduce costs but avoid lost sales and profit.
A supermarket can also use this technique to estimate queues with predicted length of waiting time determining the number of staff required.
