
(a) (0 Outline two types of quantitative methods as applied in statistics. (2 marks)
(ii) Differentiate between temporal and spatial classification methods of data. (4 marks)
(b) Explain each of the following terms as applied in sampling:
(i) population; (2 marks)
(ii) statistic; (2 marks)
(iii) parameter. (2 marks)
(c) Table 1 shows the price of different commodities and their corresponding quantities sold in two years. Use it to answer the question that follows
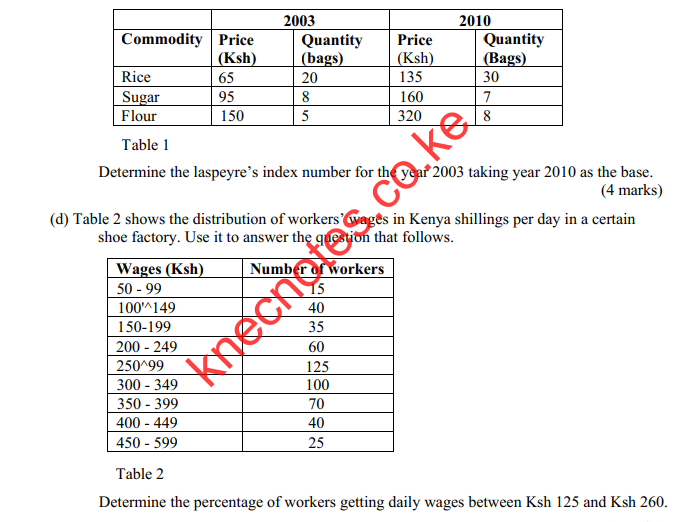
(ii) Explain two types of data tabulations as applied in data collection. (4 marks)
(b) Johnny went for an interview and the interviewer told him that the mean annual income of the 25 employees of the company is Ksh. 60,849. The actual income in Ksh for the employees is;

(i) Determine the mean; mode and median of the employee’s income; (3 marks)
(ii) State whether the interviewer was correct. (1 mark)
(c) With the aid of diagrams, distinguish between the terms skewness and kurtosis as measures of dispersion. (4 marks)
(d) (i) Lucy calculated the mean deviation of marks in percentage in a mathematics exam and got 3.75. Interpret this value. (2 marks)
(ii) In a certain college, it is known that 40% of the students are girls and 50% of students are above the median height. Two thirds of the boys are above the median height.
I. Present this information using a contingency table of probabilities. (2 marks)
II. Determine the probability that a randomly selected student who is below the median height is a girl. (2 marks)
3. (a) (i) Define the term simple index number as used in statistics. (2 marks)
(ii) Explain three factors that should be considered in the construction of an indexnumber. (6 marks)
(b) Table 3 shows the production of maize flour in thousand tonnes from a certain miller for six years.
Use it to answer the question that follows.
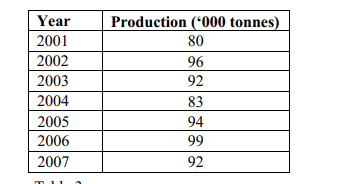
Using the least square method, determine the equation of the straight-line trend. (4 marks)
(c) Newton intends to carry out a research using the simple random sampling method to collect the data. Outline the steps he would follow. (2 marks)
(d) Cyrus, the examinations officer in Gitweh Commercial College intends to prepare a report on the performance of the students in exams and has been provided with the following data;
Out of 350 male candidates who are below 20 years of age, 50 passed;
110 male candidates who are above 20 years of age, 90 failed;
Out of 50 female candidates who are below 20 years of age, 10 passed;
Of the 34 female candidates who are over 20 years of age, 26 failed.
You have been requested to assist Cyrus to present the information in a tabular form. (6 marks)
4 (a) Outline two advantages and two disadvantages of moving averages as a method of measuring secular trends in time series. (4 marks)
(b) (i) Differentiate between the terms correlation and regression as used in statistics. (4 marks)
(ii) An agriculturalist used the Karl Pearson’s coefficient of correlation method to determine the relationship between the amount of fertilizers per unit crop yield per area of land and the unit area of land. He got a figure of 0.994. Interpret this value. (2 marks)
(c) Describe each of the following sampling methods as applied in statistics:
(i) stratified; (3 marks)
(ii) multi-stage. (3 marks)
(d) Table 4 shows the weight of children recorded in a certain clinic in one day. Use it to answer the question that follows.
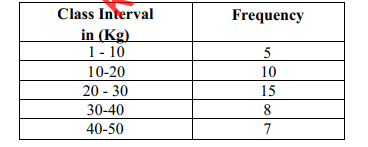
Draw a cumulative frequency curve. (4 marks)
5. (a) Explain each of the following components of time series using a sketch in each case.
(i) trend;
(ii) cyclical variation.
(b) Table 5 shows the cost of advertising a product and the corresponding sales realised.
Use it to answer the questions that follow.
Jan Feb March April May
Cost of advertising (‘000) 10 12 15 23 20
Sales realised (‘000) 14 17 23 25 21
Table 5
(i) Determine the regression equation of X (cost of advertising) on Y (Sales realised). (4 marks)
(ii) Using the equation in (i) calculate the expected sales for the same year for the month of June, given that the company’s budget to advertise in June is ksh. 300,000. (2 marks)
(c) Table 6 shows 12 activities and their duration in days for a certain project. Use it to answer the questions that follow.
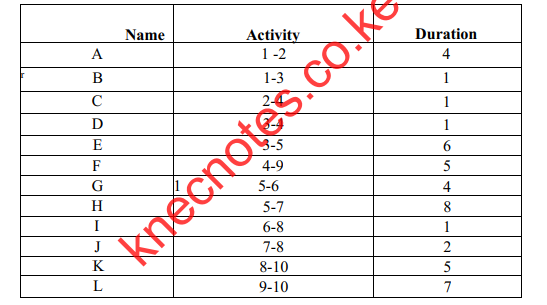
(i) Construct a PERT network; (2 marks)
(ii) Determine the Earliest Start Time (Te) and Latest Start Time (TL ) for each activity; (6 marks)
(iii) Determine the critical path. (2 marks)
6 (a) (i) Define the term coefficient of variation as used in measures of dispersions

Determine the inter-quartile range of the students’ age. (4 marks)
(b) Define each of the following terms as used in probability;
(i) equally likely events; (2 marks)
(ii) independent events; (2 marks)
(iii) random experiment. (2 marks)
(c) There are fourteen girls and twenty-three boys in a class. The class is to send four representatives to a Maths contest. The members of the class decide to send two girls and two boys. Determine the number of different groupings that are possible. (2 marks)
(d ) Esther was given three sets of data represented by the three bar graphs as shown below;
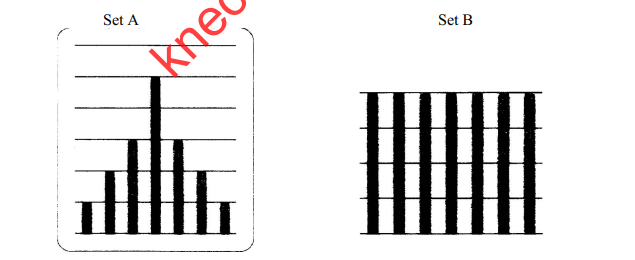
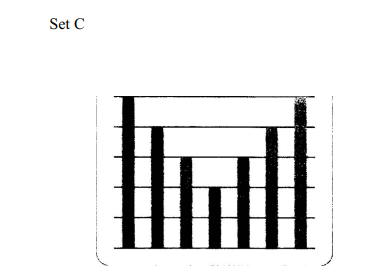
Assuming that the mean of each set is 4, Show by calculation that set A has the smallest standard deviation and set C has the largest Standard deviation. (6 marks)
7. (a) Explain the meaning of quantitative method as applied in statistics. (2 marks)
(b) The revenue function of a product is r = 28q — q 2 , the unit variable cost is v=q-8 and q is the quantity while the fixed cost is Ksh 64. Determine each of the following:
(i) total cost function; (2 marks)
(ii) profit function; (2 marks)
(iii) Show that the output for maximum profit is not necessarily the same as the output for maximum revenue. (4 marks)
(c) A committee of 8 lecturers is to be formed out of 6 Science, 8 Arts teachers and a
Physical instructor. Determine the number of ways the committee can be formed if:
(i) any teacher can be included in the committee; (2 marks)
(ii) there should be 3 science and 4 arts teachers in the committee. (4 marks)
(d) Rogers intends to invest a sum of Ksh 10,000 at an interest rate of 8.5 % per year.
Determine the amount of money that he will have after 3 years. (4 marks)
8. (a) Define each of the following measures as used in statistics:
(i) harmonic mean; (2 marks)
(ii) geometric mean. (2 marks)
(b) Table 8 shows the percentage (%) increase in the cost of living over a period of 5 years in a certain country. Use it to answer the question that follows
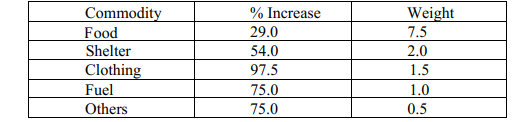
Table 8
Determine the weighted average mean of the increase in the cost of living. (4 marks)
(c) (i) A bag contains 15 coupons marked with numbers 1 to 15. One coupon is drawn at random. Determine the probability that the number marked on the coupon is:
I. greater than 10; (2 marks)
II. is a multiple of 2 or 5. (2 marks)
(ii) A certain shoe manufacturing company intends to invest in a machine that would give a profit of Ksh 100,000 annually for 10 years starting at the end of the first.
The interest rate is 5% p.a. while the maintenance cost of the machine is Ksh 5,000 Every time at the end of the first year and the end of the fifth year.
Determine the net present value of the machine. (6 marks)
(d) Identify four emerging trends and issues in quantitative methods
