
(a) A telecommunications firm has a total staff who are deployed in various departments as shown below:
Department Male Female
Marketing 180 240
Production 120 150
Finance 80 60
Human resource 60 20
Present this information using;
(i) cluster (grouped) column chart;
(ii) component bar chart;
(iii) percentage component bar chart. (12 marks)
(b) Explain two circumstances for each of the following about measures of central tendency:
(i) The mean would be preferred over the median;
(ii) The median would be preferred over the mean. (8 marks)
(a) Outline four desirable qualities of a good average. (4 marks)
(b) Describe each of the follow ing sampl ing techniques as used in the collection of statistical data:
(i) Stratified random sampling;*
(ii) Multi-stage sampling. (6 marks)
(c) A basket contains 12 red apples and 8 green apples which arc identical in all aspects except colour. John picked 3 apples from the basket at random with replacement.
(i) Present this information using a probability tree diagram. (4 marks)
(ii) Determine the probability that ail the apples picked are of the same colour.
(2 marks)
(iii) Determine the probability that of the three apples picked, the last two are of the same colour. (4 marks)
3. (a) Describe the four components of time series as applied in statistics. (12 marks)
(b) A private university has analysed its past records and derived its total cost function as C (x) = 2x + 11 and the total revenue function as R(x) = I4x x~ — 9 w’here x is the total student enrolment in thousands, while the values of cost, revenue and profit are in million Kenya shillings. Determine each of the following about the university:
(i) The total profit function given that profit P(x) = R(x) C(v);
(ii) The break-even point(s) of production;
(iii) The student enrolment that maximises profit and the corresponding profit. {8 marks)
4. (a) Define the term time series as used in statistics. (2 marks)
(b) Outline three properties of the least squares regression line as applied in statistics. (6 marks)
(c) The data in Table 1 represents the frequency distribution of marks scored by a random sample of 800 students who sat for Mathematics examination in the year 2015.
Table 1
(i) Estimate by calculation each of the following measures aboul the marks distribution:

I. Median;
II. Standard deviation. (7 marks)
(ii) The top 12% of the students are supposed to score a Distinction Grade in this exam. Determine the minimum mark for a candidate to score a Distinction
Grade. (2 marks)
(iii) Compute the Pearson’s co-efficient of skewness, and hence identify the type of skewness of this distribution. (3 marks)
5. (a) The following are examples of scales used for measuring statistical data. Classify them into the following measurement scales: nominal, ordinal, interval and ratio:
• sex as male and female;
number of vehicles passing a roadblock;
• temperature in degrees Celsius;
• weight of patients in kgs at a clinic;
• grades of students in an exam;
• longitude of a place on earth;
• job satisfaction as low, medium or high;
• numbers on the back of players in a football match.
(b) A research study was carried out on employed staff aged 50 to 70 years to assess the relationship between age of staff and their performance. The performance of each employee was quantified on a scale of 20 to 50 as shown in Table 2. Use it to answer the questions that follow.

(i) Determine the Spearman’s rank co-efficient of correlation between the age of staff and their performance. (7 marks)
(ii) Interpret the result obtained in (i). (3 marks)
(c) (i) Peter has a rental house which appreciates at a compound interest rate of 4.5% p.a. Given that the current value of the house is 10 million shillings, determine the future value of the house in 6 years. (3 marks)
(ii) John has a lorry currently valued at 8 million shillings. The lorry depreciates al a reducing balance rate of 7.5% p.a. Determine the residual value of the lorry after
6 years. (3 marks)
6. (a) Define the term questionnaire as used in statistics. (2 marks)
(b) Explain three reasons why most scientific research studies prefer sampling to census in the collection of data. (6 marks)
(c) A road construction company has been contracted by the government to repair a certain road connecting two towns. The repair project has been broken down into identifiable activities with their preceding activities and durations as shown in Table 3
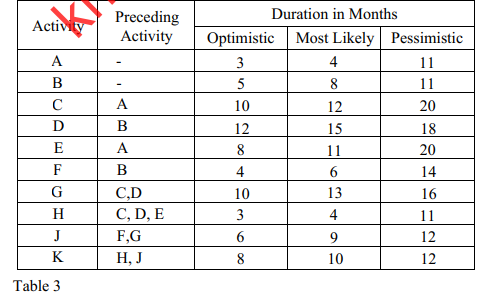
(i) Determine the expected duration for each activity. (2 marks)
(ii) Construct a network to represent the data in Table 3. (3 marks)
(iii) Determine the critical path of the network and the expected project duration. (3 marks)
(iv) Determine the probability of completing the project in 55 months. (4 marks)
7. (a) Differentiate between /im/ base and chain base methods used in the calculation of index numbers. (4 marks)
(b) A mobile phone network in Kenya uses a 10 digit code to assign phone numbers to its subscribers. The numbers must satisfy the following conditions:
• the first digit must be a zero;
• the second digit must be a 7;
• the third digit must be any of the following 0, 1,2, 3 or 4;
• the fourth digit can be any numeric digit;
• the fifth digit can be any numeric digit but not a zero;
• the 6th
, 7th
, 8th
, 9tb
and 10th digits can be any numeric digit;
Determine the maximum number of subscribers which this network can accommodate. (6 marks)
(c) It has been observed that a certain road has 2 potholes for every 150 metres along the road. A random length of 540 metres is selected from a section of the road.
(i) Derive the Poisson probability mass function for this distribution; (2 marks)
(ii) Determine the probability that from the length selected, there are:
I. exactly 5 potholes;
II. between 3 and 6 potholes inclusive;
III. at least 4 potholes. (8 marks)
8. (a) Define the term variable as used in statistics. (2 marks)
(b) Distinguish between each of the following variables as used in statistics:
(i) dependent variable and independent variable;
(ii) categorical variable and numerical variable. (8 marks)
(c) A sacco member took a loan of Ksh 800,000 repayable in a period of 5 years with an interest of 3.25% compounded monthly. Determine the total amount that he paid after the 5 years. (4 marks)
(d) The data in Table 4 shows the wage in Ksh ‘000’ for employees of a certain organisation over a six year period.
Table 4
Year 2010 2011 2012 2013 2014 2015
Wage 28 32 33 35 37 40
Consumer Price Index 102 103 105 108 114 117
Compute the real monthly wage index for each year for the employees. (6 marks)
