
3.3.2 Mathematics Alt. A Paper 2 (121/2)
SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.
1 The lengths of two similar iron bars were given as 12.5 m and 9.23 m. Calculate the maximum possible difference in length between the two bars. (3 marks)
2 The first term of an arithmetic sequence is —7 and the common difference is 3.
(a) List the first six terms of the sequence; (1 mark)
(b) Determine the sum of the first 50 terms of the sequence. (2 marks)
3 In the figure below, BOD is the diameter of the circle centre O. Angle ABD = 30° and angle AXD = 70°.
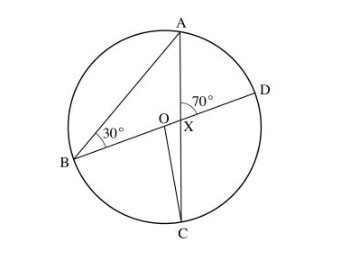
(a) reflex angle BOC; (2 marks)
Determine the size of:
(b) angle ACO. (1 mark)
4 Three quantities L, M and N are such that L varies directly as M and inversely as the square of N. Given that L = 2 when M = 12 and N = 6, determine the equation connecting the three quantities. (3 marks)
5 The table below shows the frequency distribution of marks scored by students in a test.
imageeeeee Determine the median mark correct to 2 s.f (4 marks)
6 Determine the amplitude and period of the function, y I 2 cos (3): — 45)°. (2 marks)
7 In a transformation, an object with an area of 5cm2 is mapped onto an image whose area is 30 cm. Given that the matrix of the transformation is
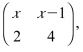
find the value of x. (3 marks)
8 Expand (3 — x)’ up to the term containing x‘. Hence find the approximate value of (2.8)7. (3 marks)
9 Solve the equation;
2 log 15 — log x I log 5 + log (x — 4). (4 marks)
10 The figure below represents a cuboid PQRSTUVW.
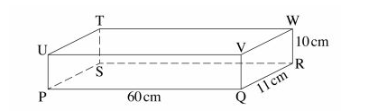
Calculate the angle between line PW and plane PQRS, correct to 2 decimal places. (3 marks)
ll Solve the simultaneous equations;
3x I y I 9
x2 — xy I 4 (4 marks)
12 Muga bought a plot of land for Ksh 280000. After 4 years, the value of the plot was Ksh 495 000. Determine the rate of appreciation, per annum, correct to one decimal place. (3 marks)
13 The shortest distance between two points A (40 °N, 20 °W) and B (6 °S, 20 °W) on the surface of the earth is 8008 km. Given that the radius of the earth is 6370km, determine the position of B.
(Take TE = 22/7 ). (3 marks)
14 Vectors r and s are such that r=7i+2j—k and s=—i+j—k.Find|r+s|. (3 marks)
15 The gradient of a curve is given by
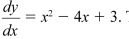
. The curve passes through the point (1,0). Find the equation of the curve. (3 marks)
16 The graph below shows the rate of cooling of a liquid with respect to time.
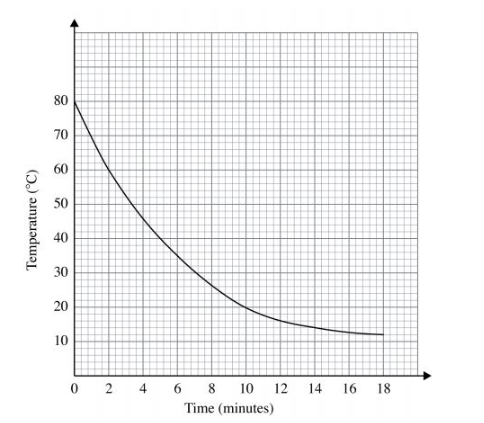
Determine the average rate of cooling of the liquid between the second and the eleventh minutes. (3 marks)
SECTION ll (50 marks)
Answer only five questions in this section in the spaces provided.
17 A paint dealer mixes three types of paint A, B and C, in the ratios A:B = 3:4 and B:C = 1:2.
The mixture is to contain l68 litres of C.
(a) Find the ratio A:B:C. (2 marks)
(b) Find the required number of litres of B. (2 marks)
(c) The cost per litre of type A is Ksh 160, type B is Ksh 205 and type C is Ksh 100.
(i) Calculate the cost per litre of the mixture. (2 marks)
(ii) Find the percentage profit if the selling price of the mixture is Ksh 182 per litre. (2 marks)
(iii) Find the selling price of a litre of the mixture if the dealer makes a 25% profit. (2 marks)
18 In the figure below OS is the radius of the circle centre O. Chords SQ and TU are extended to meet at P and OR is perpendicular to QS at R. OS = 61 cm, PU = 50 cm, UT = 40cm and PQ = 30cm.
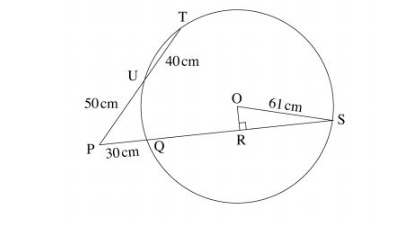
(a) Calculate the length of:
(i) QS; (2 marks)
(ii) OR. (3 marks)
(b) Calculate, correct to 1 decimal place:
(i) the size of angle ROS; (2 marks)
19 The table below shows income tax rates for a certain year.
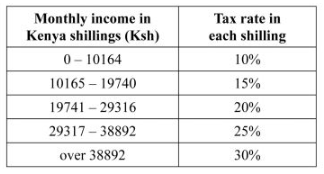
A tax relief of Ksh 1 162 per month was allowed. In a certain month, ofthat year, an employee’s taxable income in the fifth band was Ksh 2108.
(a) Calculate:
(i) the employee’s total taxable income in that month; (2 marks)
(ii) the tax payable by the employee in that month. (5 marks)
(b) The employee’s income included a house allowance of Ksh 15 000 per month.
The employee contributed 5% of the basic salary to a co-operative society.
Calculate the employees net pay for that month. (3 marks)
20 The dimensions of a rectangular floor of a proposed building are such that:
- the length is greater than the width but at most twice the width;
- the sum of the width and the length is, more than 8 metres but less than 20 metres. if x represents the width and y the length.(a) write inequalities to represent the above information. (4 marks)
(b) (i) Represent the inequalities in part (a) above on the grid provided. (4 marks)
(ii) Using the integral values of x and y, find the maximum possible area of the floor. (2 marks)
21 Each morning Gataro does one of the following exercises:
Cycling, jogging or weightlifting.
He chooses the exercise to do by rolling a fair die. The faces of the die are numbered 1,1,2, 3, 4 and 5.
If the score is 2, 3 or 5, he goes for cycling.
If the score is 1, he goes for jogging.
If the score is 4, he goes for weightlifting.
(a) Find the probability that:
(i) on a given morning, he goes for cycling or weightlifiing; (2 marks)
(ii) on two consecutive mornings he goes for jogging. (2 marks)
(b) In the afternoon, Gataro plays either football or hockey but never both games. The probability that Gataro plays hockey in the afternoon is:
% if he cycled;
% if he jogged and
% if he did weightlifting in the morning.
Complete the tree diagram below by writing the appropriate probability on each branch. (2 marks)
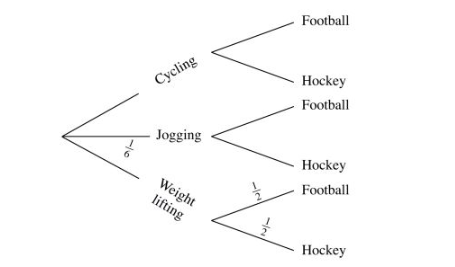
(c) Find the probability that on any given day:
(i) Gataro plays football; (2 marks)
(ii) Gataro neither jogs nor plays football. (2 marks)
22 In the figure below OA = a and OB = b. M is the mid-point of OA and AN:NB = 2:1.
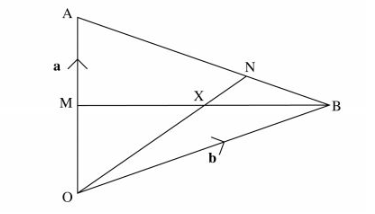
(a) Express in terms of a and b:
(i) BA; (1 mark)
(ii) BN; (1 mark)
(iii) ON. (2 marks)
(b) Given that BX = hBM and OX = kON determine the values of h and k. (6 marks)
23 Figure ABCD below is a scale drawing representing a square plot of side 80 metres.
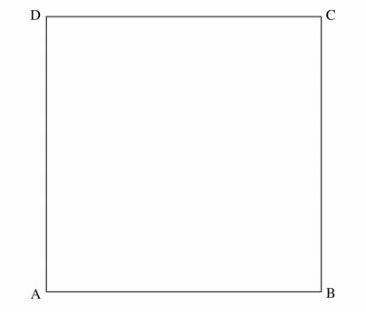
(a) On the drawing, construct:
(i) the locus of a point P, such that it is equidistant from AD and BC. (2 marks)
(ii) the locus of a point Q such that LAQB = 60°.
(b) (i) Mark on the drawing the point Q], the intersection of the locus of Q and line AD. ‘ k
Determine the length of BQ1, in metres. (1 mark )
(ii) Calculate, correct to the nearest m2, the area of the region bounded by the locus of ‘ (4 marks)
P, the locus of Q and the line BQI.
24 In an experiment involving two variables t and r, the following results were obtained.

(a) On the grid provided, draw the line of best fit for the data. (4 marks)
(b) The variables r and t are connected by the equation r = at + k where a and k are constants.
Determine:
(i) the values of a and k; (3 marks)
(ii) the equation of the line of best fit. (1 mark)
(iii) the value of t when r = 0. (2 marks)
