
KCSE Past Papers Maths A 2014
Section 1 (50 marks)
Answer all the questions in this section in the spaces provided.
1 Ntutu had cows, sheep and goats in his farm. The number of cows was 32 and number of sheep was twelve times the number of cows. The number of goats was 1344 more than the number of sheep. If he sold % of the goats, find the number of goats that remained. (4 marks)
2 Use the prime factors of 1764 and 2744 to evaluate
(3 marks)
3 The mass of a solid cone of radius 14 cm and height 18 cm is 4.62 kg. Find its density in g/cm}. (3 marks)
4 The figure below represents a triangular prism ABCDEF. X is a point on BC.
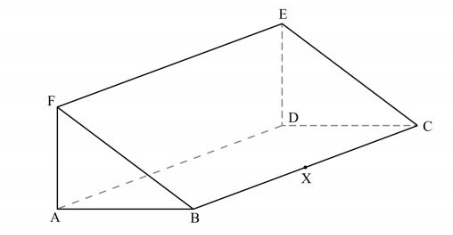
(a) Draw a net of the prism. (2 marks)
(b) Find the distance DX. (1 mark)
5 A businessman makes a profit of 20% when he sells a carpet for Ksh 36 000. In a trade fair he sold one such carpet for Ksh 33 600. Calculate the percentage profit made on the sale of the carpet during the trade fair. (3 marks)
6 Simplify
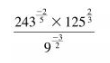
(3 marks)
7 The area of a sector of a circle, radius 2.1 cm, is 2.31 cml. The arc of the sector subtends an angle 6, at the centre of the circle. Find the value of 6 in radians correct to 2 decimal places. (2 marks)
8 Expand and simplify
![]()
(2 marks)
9 A plane leaves an airstrip L and flies on a bearing of 040° to airstrip M, 500km away. The plane then flies on a bearing of 3 16° to airstrip N. The bearing of N from L is 350°. By scale drawing, determine the distance between airstrips M and N. (4 marks)
10 The sum of interior angles of a regular polygon is 1800 °. Find the size of each exterior angle. (3 marks)
11 A cow is 4 years 8 months older than a heifer. The product of their ages is 8 years. Determine the age of the cow and that of the heifer. (4 marks)
12 Solve 4 S 3x — 2 < 9 + x hence list the integral values that satisfies the inequality. (3 marks)
13 The figure below shows a rectangular container of dimensions 40cm by 25 cm by 90cm. A cylindrical pipe of radius 7.5 cm is fitted in the container as shown.
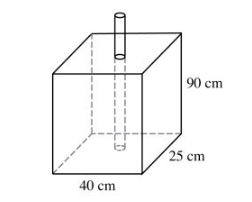
Water is poured into the container in the space outside the pipe such that the water level is 80% the height of the container. Calculate the amount of water, in litres, in the container correct to 3 significant figures. (4 marks)
14 A minor are of a circle subtends an angle of 105° at the centre of the circle. if the radius of the circle is 8.4 cm, find the length of the major arc. imageeeee (3 marks)
15 Twenty five machines working at a rate of 9 hours per day can complete a job in 16 days. A contractor intends to complete the job in 10 days using similar machines working at a rate of 12 hours per day. Find the number of machines the contractor requires to complete the job. (3 marks)
16 Points A (— 2, 2) and B (— 3, 7) are mapped onto A’ (4, — 10) and B’ (0, 10) by an enlargement. Find the scale factor of the enlargement. (3 marks)
SECTION ll (50 marks)
Answer only five questions in this section in the spaces provided.
17 A line L passes through points (— 2. 3) and (— 1, 6) and is perpendicular to a line P at (— 1, 6).
(a) Find the equation of L. (2 marks)
(b) Find the equation of P in the form ax + by = c, where a, b and c are constants. (2 marks)
(c) Given that another line Q is parallel to L and passes through point (1, 2), find the x and y intercepts of Q. (3 marks)
(d) Find the point of intersection of lines P and Q. (3 marks)
18 The lengths, in cm, of pencils used by pupils in a standard one class on a certain day were recorded as follows.

(a) Using a class width of 3, and starting with the shortest length of the pencils, make a frequency distribution table for the data. (2 marks)
(b) Calculate:
(i) the mean length of the pencils; (3 marks)
(ii) the percentage of pencils that were longer than 8 cm but shorter than 15 cm. (2 marks)
(c) On the grid provided, draw a frequency polygon for the data. (3 marks)
19 The figure below represents a speed time graph for a cheetah which covered 825 m in 40 seconds.
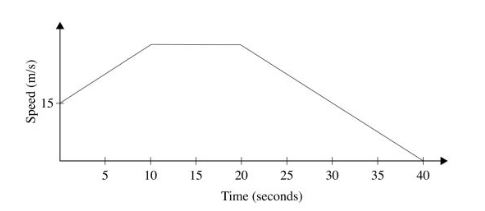
(a) State the speed of the cheetah when recording of its motion started.(1 mark) (b) Calculate the maximum speed attained by the cheetah.(3 marks) (c)Calculate the acceleration of the cheetah in:(2 marks) (i) the first 10 seconds;(1 mark) (ii) the last 20 seconds.(2 marks) Calculate the average speed of the cheetah in the first 20 seconds.(3 marks)
20 The figure below shows a right pyramid VABCDE. The base ABCDE is a regular pentagon. AO = 15cm and VO = 36cm.(3 marks)
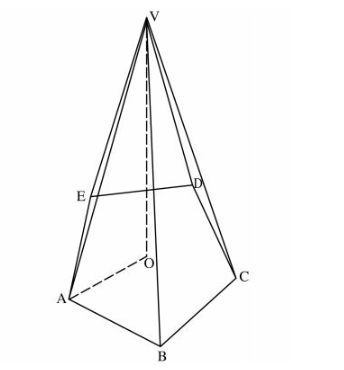
Calculate:
(a) the area of the base correct to 2 decimal places; (3 marks)
(b) the length AV; (1 mark)
(c) the surface area of the pyramid correct to 2 decimal places; (4 marks)
(d) the volume of the pyramid correct to 4 significant figures. (2 marks)
21 (a)

22 (a) Using a pair of compasses and ruler only, construct:
(i) triangle ABC in Which AB = 5cm, LBAC = 30° and LABC = 105°; (3 marks)
(ii) a circle that passes through the vertices of the triangle ABC. Measure the radius. (3 marks)
(iii) the height of triangle ABC with AB as the base. Measure the height. (2 marks)
(b) Determine the area of the circle that lies outside the triangle correct to 2 decimal places. (2 marks)
23 The figure below represents a piece of land in the shape of a quadrilateral in which AB = 240m, BC = 70 m, CD = 200m, LBCD = 150° and LABC I 90°.
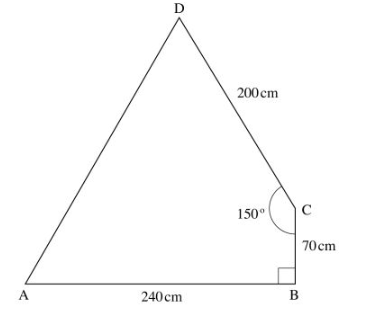
Calculate:
(a) the size of LBAC correct to 2 decimal places; (2 marks)
(b) the length AD correct to one decimal place; (4 marks)
(c) the area of the piece of land, in hectares, correct to 2 decimal places. (4 marks)
24 The equation of a curve is given by
(a) Find the value of y when x = -1. (1 mark)
(b) Determine the stationary points of the curve. (5 marks)
(c) Find the equation of the normal to the curve at x = 1.
