
KCSE Past Papers Maths A 2013
MATHEMATICS ALT. A (121)
Mathematics Alt. A Paper 1 ( 121/1)
SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.
1 Evaluate
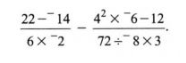
(2 marks)
2 The production of milk, in litres, of 14 cows on a certain day was recorded as follows: 22, 26, 15, 19, 20,16, 27,15, 19, 22, 21, 20, 22 and 28. Determine:
(a) the mode; (1 mark)
(b) the median. (2 marks)
3 Use logarithms, correct to 4 decimal places, to evaluate

(4 marks)
5. A wholesaler sold a radio to a retailer making a profit of 20%. The retailer later sold the radio for Ksh 1560 making a profit of 30%. Calculate the amount of money the wholesaler had paid for the radio. (3 marks)
6 A point P on the line AB shown below is such that AP = %AB. By construction locate P. (3 marks)

7 Chelimo’s clock loses 15 seconds every hour. She sets the correct time on the clock at 0700h on a Monday. Determine the time shown on the clock when the correct time was 1900h on Wednesday the same week. (3 marks)
8 Given that sin (x + 20)° = — 0.7660, find x, to the nearest degree, for 0°< x <360°. (3 marks)
9 A number m is formed by writing all the prime numbers between 0 and 10 in an ascending order. Another number n is formed by writing all the square numbers between 0 and 10 in a descending order.
(a) Find m — n; (2 marks)
(b) Express (m — n) as a product of its prime factors. (1 mark)
10 The figure below shows a net of a solid. (Measurements are in centimetres).
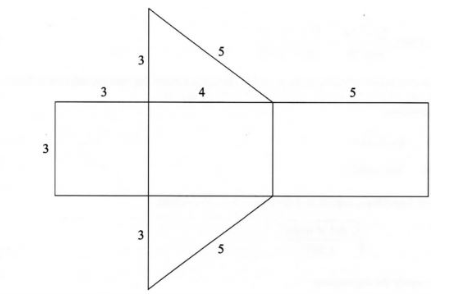
Below is a part of the sketch of the solid whose net is Shown above. Complete the sketch of the solid, showing the hidden edges with broken lines. (3 marks)
11 The interior angles of an octagon are 2x, 1/2x, (x + 40)°, 110°, 135°, 160°, (2x + 10)° and 185°. Find the value of x. (2 marks)
12 A straight line passes through points (-2, 1) and (6, 3). Find: (a) the equation of the line in the form y = mx + c; (2 marks)
(b) the gradient of a line perpendicular to the line in (a). (1 mark)
13 A triangle ABC is such that AB = 5 cm, BC = 6cm and AC = 7cm.
(a) Calculate the size of angle ACB, correct to 2 decimal places. (2 marks)
(b) A perpendicular drawn from A meets BC at N. Calculate the length AN correct to one decimal place. (2 marks)
14 A cylindrical pipe 2 1/2 metres long has an internal diameter of 21 millimetres and an external diameter of 35 millimetres. The density of the material that makes the pipe is 1.25 g/cm‘. Calculate the mass of the pipe in kilograms. (Take n = 22/7). (4 marks)
15 The figure below represents a pentagonal prism of length 12cm. The cross-section is a regular pentagon of side 5 cm.
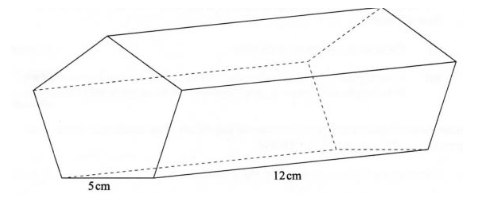
Calculate the surface area of the prism correct to 4 significant figures. (4 marks)
Given the inequalities x — 5 < 3x — 8 < 2x — 3.
(a) Solve the inequalities; (2 marks)
(b) represent the solution on a number line. (1 mark)
SECTION ll (50 marks)
Answer only five questions in this section in the spaces provided.
17 A farmer had 540 bags of maize each having a mass of 112 kg. After drying the maize, the mass decreased in the ratio 15: l 6.
(a) Calculate the total mass lost after the maize was dried. (3 marks)
(b) A trader bought and repacked the dried maize in 90 kg bags. He transported the maize in a lorry which could carry a maximum of 120 bags per trip.
(i) Determine the number of trips the lorry made. (3 marks)
(ii) The buying price of a 90 kg bag of maize was Ksh 1500. The trader paid Ksh 2500 per trip to transport the maize to the market. He sold the maize and made a profit of 26%. Calculate the selling price of each bag of the maize.
(4 marks)
18 (a) Solve the equation, x + 3/24 = 1/x-2 (4 marks) (b) The length of a floor of a rectangular hall is 9m more than its width. The area of the floor is 136 ml. (i) Calculate the perimeter of the floor. (4 marks)
(ii) A rectangular carpet is placed on the floor of the hall leaving an area of 64 mi. If the length of the carpet is twice its width, determine the width of the carpet. (2 marks)
19 A trader bought 2 cows and 9 goats for a total of Ksh 98 200. If she had bought 3 cows and 4 goats she would have spent Ksh 2200 less.
(a) F om1 two equations to represent the above information. (2 marks)
(b) Use matrix method to determine the cost of a cow and that of a goat. (4 marks)
(c) The trader later sold the animals she had bought making a profit of 30% per cow and 40% per goat.
(i) Calculate the total amount of money she received. (2 marks)
(ii) Determine, correct to 4 significant figures, the percentage profit the trader made from the sale of the animals. (2 marks)
20 Two towns, A and B are 80 km apart. Juma started cycling from town A to town B at 10.00 am at an average speed of 40 km/h. Mutuku started his journey from town B to town A at 10.30 am and travelled by car at an average speed of 60 km/h.
(a) Calculate:
(i) the distance from town A when Juma and Mutuku met; (5 marks)
(ii) the time of the day when the two met. (2 marks)
(b) Kamau started cycling from town A to town B at 10.21am. He met Mutuku at the same time as Juma did. Determine Kamau’s average speed. (3 marks)
21 The displacement, s metres, of a moving particle from a point O, after t seconds is given by, s=t2—5t2 +3t + 10.
(a) Find s when t = 2.(2 marks)
(b) Determine:
(i) the velocity of the particle when t = 5 seconds;(3 marks)
(ii) the value of t when the particle is momentarily at rest.(3 marks)
(c) Find the time, when the velocity of the particle is maximum.(2 marks)
22 In the figure below, OABC is a trapezium. AB is parallel to OC and OC = SAB. D is a point on OC such that OD: DC = 3:2.
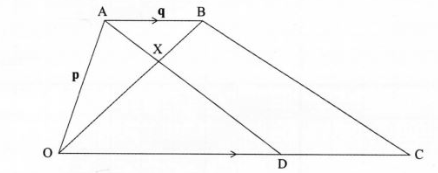
(a) Given that OA = p and AB = q, express in terms of p and q:
(i) OB;(1 mark)
(ii) AD;(2 marks)
(iii) CB.(2 marks)
(b) Lines OB and AD intersect at point X such that AX = kAD and OX = rOB, where k and r are scalars. Determine the values of k and r.
(5 marks)
23 (a) On the grid provided, draw the square whose vertices are A (6, -2), B (7, -2), C(7,— 1)andD(6,— 1). (1 mark)
On the same grid below, draw: (ii) A”B”C”D”, the image of A’B’C’D’ under a reflection in the line x = 0; (2 marks)
(iii) A'”B”’C”‘D’”, the image of A”B”C”D” under a rotation of +90° about (0,0). (2 marks)
(c) Describe a single transformation that maps A’B’C’D’ onto A”’B’”C’”D”’. (2 marks)
24 The figure below represents a cone of height 12 cm and base radius of 9 cm from which a similar smaller cone is removed, leaving a conical hole of height 4 cm.
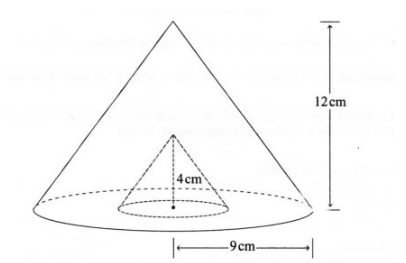
(a) Calculate:
(i) the base radius of the conical hole; (2 marks)
(ii) the volume, in terms of 11:, of the smaller cone that was removed. (2 marks)
(b) (i) Determine the slant height of the original cone. (1 mark)
(ii) Calculate, in terms of 1:, the surface area of the remaining solid after the smaller cone is removed. (5 marks)
