MONDAY: 17 May 2021. Time Allowed: 3 hours.
Answer ALL questions. Marks allocated to each question are shown at the end of the question. Show ALL your workings.
QUESTION ONE
1. Summarise live reasons why financial analysts create a financial model of an entity while undertaking their assignments. (5 marks)
2. Describe four finance functions in an organisation. (8 marks)
3. Abdi Hassan is considering two investment plans; A and B.
Investment A has equal annual returns of Sh.700,000 for a period of 6 years.
Investment B has unequal annual returns over the same period of years as follows:
Year 1 2 3 4 5 6
Returns (Sh.) 550,000 600,000 700,000 900.000 850.000 650.000
The appropriate discount rate of each investment is 14%.
Required:
Using the net present value (NPV) approach, recommend the investment to undertake. (7 marks)
(Total: 20 marks)
QUESTION TWO
1. A manufacturer determines demand of one of its products to be P = 60 — 3Q.
Where: P is the price in shillings per unit and
Q is the quantity in millions annually.
The average cost of the product is given by the function:
![]()
Required:
Total cost function. TC. (2 marks)
Total revenue function, TR. ( 1 mark)
An expression for marginal cost (MC) and its value when Q = 3. (4 marks)
The level of Q when profit is maximised. (3 marks)
The level of profit/loss. Justify your answer. (4 marks)
2. The weekly prices of shares A and B in the Securities Exchange of your country were as follows:
Share A Probability Share 13 Probability
100 0.10 250 0.25
300 0.20 300 0.10
330 0.40 400 0.40
470 0.20 520 0.10
500 0.10 600 0.15
Required:
The mean price of each share during the week. (2 marks)
The standard deviation of each share during the week. (4 marks)
(Total: 20 marks)
QUESTION THREE
1. Outline four basic assumptions of binomial distribution theorem. (4 marks)
2. Invoices at a particular pharmacy have amounts which follow a normal distribution with a mean of Sh.103.60 and a standard deviation of Sh.8.73.
Required:
Determine the percentage of invoices that would be:
Over Sh.120.05 (2 marks)
Below Sh.72.75 (2 marks)
Between Sh.83.65 and Sh.117.60 (3 marks)
3. The table below shows the frequency distribution of marks on a Financial Mathematics examination:
Marks 30-39 40-49 50-59 60-69 1 70-79 80-89 90-100
Frequency 10 32 44 20 I 12 1 1
Required:
The mean mark. ( 1 mark)
The median mark. (2 marks)
The mode. (2 marks)
The relative frequency of the modal class. ( 1 mark)
The standard deviation. (3 marks)
(Total: 20 marks)
QUESTION FOUR
1. Explain four components of a time series. (4 marks)
2. A financial analyst plans to investigate whether there exists a relationship between maintenance cost of a fleet of vehicles and their age. Data relating to maintenance cost with respect to age of the vehicles availed by the cost accountant is as follows:
Age (Years) 5 8 10 12 15 17 19 20
Maintenance cost (per month) 12 14 14 15 17 25 30 35
Sh. (000)
Required:
The product moment correlation coefficient. (5 marks)
The regression equation explaining monthly maintenance cost as a function of age. (4 marks)
3. Dalton Abuga borrows Sh.100,000 from a financial institution to improve his business. The loan is payable in equal annual installments for five years. The interest rate on the loan is 14% per annum.
Required:
A loan amortisation schedule. (5 marks)
The interest payable over the life of the loan. (1 mark)
Express the interest as a percentage of the total amount paid over the life of the loan. ( 1 mark)
(Total: 20 marks)
QUESTION FIVE
1. Highlight three weaknesses of simple aggregate index as used in index numbers. (3 marks)
2. The data below relates to basic weekly wage rates (W) and the number of employees (E) in a medium construction company:
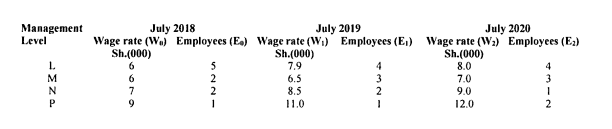
Required:
Laspeyres index number for July 2019 basic wage rates, with July 2018 = 100 (3 marks)
Paasche index number for the July 2020 basic weekly wage rates with July 2018 =100 (3 marks)
Explain why the values obtained in (i) and (ii) above are different from the official figures for the construction industry given below:
Yearly annual averages:
2018 2019 2020
Weekly wage rates
(July 2015 = 100) 156.3 187.4 203.4
(2 marks)
3. Members of a welfare society intend to invest in a project that cost Sh.1,300,320. Each member of the welfare society is to contribute an equal amount towards the project. However, before the start of the project, 8 members opted to pull out forcing the contribution on the remaining members to increase by Sh.2,257.50. The contributions are to be made over a five month period.
The welfare committee intends to recruit additional members should the cost of the project increase by over 5% of the original cost. The additional members will take up the increased cost at the same amount payable by existing members.
Required:
The number of current members in the investment project. (5 marks)
The percentage increase in contributions. (2 marks)
If the project cost increased by 6.25%, calculate the number of members to be recruited. (2 marks)
(Total: 20 marks)
