INTRODUCTION
The important message of the preceding chapter is that sound investment decisions should be based on the net present value (NPV) rule. The first difficult problem to be resolved in applying the NPV rule in practice is: What should be discounted? In theory, the answer is obvious: We should always discount cash flows. In reality, estimating cash flows is the most difficult task. The difficulty in estimating cash flows arises because of business uncertainty and accounting ambiguities. Events affecting investment opportunities change rapidly and unexpectedly. There is no easy way to anticipate changes in events. Mostly accounting data forms the basis for estimating cash flows. Accounting data are the result of arbitrary assumptions, choices and allocations in accounting. If care is not taken in properly adjusting the accounting data, errors could be made in estimating cash flows.
We consider the cash flow estimation as the most crucial step in investment analysis. A sophisticated technique applied to incorrect cash flows would produce wrong results. The management of a company should devote considerable time, effort and money in obtaining correct estimates of cash flows. The financial managers prepare the cash flow estimates on the basis of the information supplied by experts in accounting, production, marketing, economics, and so on. It is their responsibility to check such information for relevance and accuracy.
The second major problem in applying the NPV rule is: What rate should be used to discount cash flows? In principle, the opportunity cost of capital should be used as the discount rate.
CASH FLOWS vs PROFIT
Cash flow should not be confused with profit. Changes in profits do not necessarily mean changes in cash flows. It is not difficult to find examples of firms in practice that experience cash shortages in spite of increasing profits. Cash flow is not the same thing as profit, at least, for two reasons. First, profit, as measured by an accountant, is based on accrual concept—revenue (sales) is recognized when it is earned, rather than when cash is received, and expense is recognized when it is incurred rather than when cash is paid. In other words, profit includes cash revenues as well as receivables and excludes cash expenses as well as payable. Second, for computing profit, expenditures are arbitrarily divided into revenue and capital expenditures. Revenue expenditures are entirely charged to profits while capital expenditures are not. Capital expenditures are capitalized as assets (investments), and depreciated over their economic life. Only annual depreciation is charged to profit. Depreciation (DEP) is an accounting entry and does not involve any cash flow. Thus, the measurement of profit excludes some cash flows such as capital expenditures and includes some non-cash items such as depreciation.The use of NPV rule in investment decisions requires information about cash flows. It is the inflow and outflow of cash, which matters in practice. It is cash, which a firm can invest, or pay to creditors to discharge its obligations, or distribute to shareholders as dividends. Cash flow is a simple and objectively defined concept. It is simply the difference between rupees received and rupees paid out.
Let us illustrate the difference between profit and cash flow. Assume that a firm is entirely equity financed, and it receives its revenues (REV) in cash and pays its expenses (EXP) and capital expenditures (CAPEX) in cash. Also, assume that taxes do not exist. Under these circumstances, profit is equal to:
Profit = Revenues – Expenses – Depreciation
Profit = REV – EXP – DEP (1)
and cash flow is equal to:
Cash flow = Revenues – Expenses – Capital Expenditure
CF = REV – EXP – CAPEX (2)
It may be noticed from Equations (1) and (2) that profit does not deduct capital expenditures as investment outlays are made. Instead, depreciation is charged on the capitalized value of investments. Cash flow, on the other hand, ignores depreciation since it is a non-cash item and includes cash paid for capital expenditures. In the accountant’s book, the net book value of capital expenditures will be equal to their capitalized value minus depreciation.
We can obtain the following definition of cash flows if we adjust Equation (2) for relationships given in Equation (1):
CF = (REV – EXP – DEP) + DEP – CAPEX
CF = Profit + DEP – CAPEX (3)
In our discussion so far, we have assumed for simplicity an entirely equity-financed firm with no taxes. In the absence of taxes, depreciation is worthless since it has no impact on cash flows. However, it assumes relevance when taxes exist because depreciation is a deductible expense for computing taxes. Thus, it affects cash flows by saving taxes. In the next section, we show the computation of cash flows when taxes exist and the firm also employs debt.
Equation (3) makes it clear that even if revenues and expenses are expressed in terms of cash flow, still profit will not be equal to cash flows. It overstates cash inflows by excluding capital expenditures and understates them by including depreciation.1 Thus, profits do not focus on cash flows. Financial managers will be making incorrect decisions if they put emphasis on profits or earnings per share rather than cash flows. The objective of a firm is not to maximize profits or earnings per share, rather it is to maximize the shareholders’ wealth, which depends on the present value of cash flows available to them. In the absence of taxes and debt, Equation (3) provides the definition of profits available for distribution as cash dividends to shareholders. Profits fail to provide meaningful guidance for making financial decisions. Profits can be changed by affecting changes in the firm’s accounting policy without any effect on cash flows. For example, a change in the method of inventory valuation will change the accounting profit without a corresponding change in cash flows.
INCREMENTAL CASH FLOWS
It is important to note that all additional cash flows that are directly attributable to the investment project should be considered. A cash flow stream is a series of cash receipts and payments over the life of an investment. The estimates of amounts and timing of cash flows resulting from the investment should be carefully made on an incremental basis.
What do we mean by incremental cash flows? Every investment involves a comparison of alternatives. The problem of choice will arise only if there are at least two possibilities. The minimum investment opportunity, which a company will always have, will be either to invest or not to invest in a project. Assume that the question before a company is to introduce a new product. The incremental cash flows in this case will be determined by comparing cash flows resulting with and without the introduction of the new product. If, for example, the company has to spend `50,000 initially to introduce the product, we are implicitly comparing cash outlay for introducing the product with a zero cash outlay of not introducing the product. When the incremental cash flows for an investment are calculated by comparing with a hypothetical zero-cash-flow project, we call them absolute cash flows.
Assume now that the question before a company is to invest either in Project A or in
Project B. One way of analysing can be to compute the absolute cash flows for each project
and determine their respective NPVs. Then, by comparing their NPVs, a choice can be made. Alternatively, two projects can be compared directly. For example, we can subtract (algebraically) cash flows of Project B from that of Project A (or vice versa) to find out incremental cash flows (of Project A minus Project B). The positive difference in a particular period will tell how much more cash flow is generated by Project A relative to Project B. The incremental cash flows found out by such comparison between two real alternatives can be called relative cash flows.2 NPV of this series of relative cash flows will be equal to NPV of the absolute cash flows from Project A minus NPV of the absolute cash flows from Project B. Thus, NPV (A – B) = NPV (A) – NPV (B). As discussed in the preceding chapter, this is so because of the principle of value additivity. The principle of incremental cash flows assumes greater importance in the case of replacement decisions. Let us consider an example.
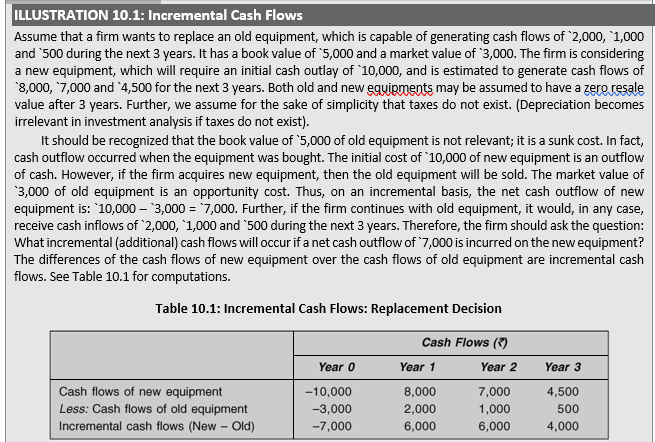
Let us relax the assumption of no resale value for old and new equipments after 3 years. Assume that the old equipment will realize `500 and new equipment `2,500 as salvage values after 3 years. If the firm goes for the new equipment, the estimated proceeds of `2,500 from its sale after 3 years is an inflow of cash; but then the firm will discard old equipment today and forgo the opportunity of realizing `500 from its sale after 3 years. As a consequence, the net cash inflow from sale proceeds after 3 years will be `2,500 – `500 = `2,000.
Check Your Concepts
- What is the difference between profit and cash flow (from operation)?
- Illustrate the concept of incremental cash flow. Why is it important in investment decisions?
COMPONENTS OF CASH FLOWS
A typical investment will have three components of cash flows:
Initial investment (cash outlay) Annual net cash flows
Terminal cash flows
Initial Investment
Initial investment is the net cash outlay in the period in which an asset is purchased. A major element of the initial investment is the gross outlay or original value (OV) of the asset, which comprises of its cost (including accessories and spare parts) and freight and installation charges. Original value is included in the existing block of assets for computing annual depreciation. Similar types of assets are included in one block of assets. Original value minus depreciation is the asset’s book value (BV). When an asset is purchased for expanding revenues, it may require a lump sum investment in net working capital also. Thus initial investment will be equal to: gross investment plus increase in net working capital. Further, in case of replacement decisions, the existing asset will have to be sold if the new asset is acquired. The sale of the existing asset provides cash inflow. The cash proceeds from the sale of the existing assets should be subtracted to arrive at the initial investment. We shall use the term C0 to represent initial investment.
Net Cash Flows
In practice, a large investment project may comprise of a number of cost components and involve a huge initial net cash outlay. A large manufacturing project may require land and site development for constructing a factory building where plant and machinery to be bought by the company will be erected.
An investment is expected to generate annual cash flows from operations after the initial cash outlay has been made. Cash flows should always be estimated on an after-tax basis. Some people advocate computing of cash flows before taxes and discounting them at the before-tax discount rate to find NPV. Unfortunately, this will not work in practice since there does not exist an easy and meaningful way for adjusting the discount rate on a beforetax basis.
We shall refer to the after-tax cash flows as net cash flows (NCF) and use the terms C1, C2, C3, … Cn respectively for NCF in period 1, 2, 3, … n. NCF is simply the difference between cash receipts and cash payments including taxes. NCF will mostly consist of annual cash flows occurring from the operation of an investment, but it is also affected by changes in net working capital and capital expenditures during the life of the investment. To illustrate, we first take the simple case where cash flows occur only from operations. Let us assume that all revenues (sales) are received in cash and all expenses are paid in cash (obviously cash expenses will exclude depreciation since it is a non-cash expense). Thus, the definition of NCF will be:
![]()
Notice that in Equation (4) taxes are deducted for calculating the after-tax cash flows. Taxes are computed on the accounting profit, which treats depreciation as a deductible expense.
Depreciation and Taxes
The computation of the after-tax cash flows requires a careful treatment of non-cash expense items such as depreciation. Depreciation is an allocation of cost of an asset. It involves an accounting entry and does not require any cash outflow; the cash outflow occurs when the assets are acquired.
Depreciation, calculated as per the income tax rules, is a deductible expense for computing taxes. In itself, it has no direct impact on cash flows, but it indirectly influences cash flow since it reduces the firm’s tax liability. Cash outflow for taxes saved is in fact an inflow of cash. The saving resulting from depreciation is called depreciation tax shield. Consider an example.
Table 10.2: Profit and Loss Account for the Investment Project

Taxes = Tax rate × Profit
Suppose that an investment requires an initial cash outlay of `50,000. It is expected to generate total annual cash sales of `25,000 and to incur total annual cash expenses of `10,000 for the next 10 years. Also, assume that an annual depreciation of `5,000 (i.e., cost recovered equally over the life of the investment) will be charged. If taxes do not exist, depreciation is of no use in computing cash flows and NCF will simply be: `25,000 – `10,000 = `15,000 per year. In practice, taxes do exist and depreciation is tax deductible. Let us assume a corporate tax rate of 35 per cent. We can recast a profit and loss account for the investment as given in Table 10.2. We see that the investment yields an annual profit of `6,500. However, this is not equal to the annual cash flow. Depreciation is a noncash item, and should be added to profit to compute actual cash flows. Thus net cash flows will be equal to: `6,500 + `5,000 = `11,500. Now we develop an analytical method for computing the net cash flows from operations. Taxes are paid on profits and can be calculated as follows:
= Tax rate × (Revenues – Expenses – Depreciation)
TAX = T (REV – EXP – DEP) (5)
where T is the corporate tax rate. Notice that the expression within brackets is the taxable income, which in our example is equal to earning before interest and taxes (EBIT), or net operating income (NOI). Thus,
Equation (5) can be rewritten as:
TAX = T (EBIT) (6)
In the example (Table 10.2), taxes are equal to:
Tax = 0.35 × 10,000 = `3,500
and using Equation (4), net cash flow from operations will be:
NCF = REV – EXP – TAX – `25,000 – `10,000 – `3,500 = `11,500
NCF can also be measured in the following way if we substitute Equation (5) into Equation (4):
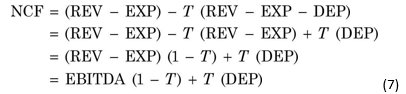
where EBITDA is earnings before, interest, taxes, depreciation and amortization. Using Equation (7), NCF is computed as follows:
![]()
It may be noted from the above computation that depreciation has provided a tax shield (DTS) equal to tax rate multiplied by the amount of depreciation: Depreciation tax shield = Tax rate × Depreciation
![]()
After-tax cash flows would have been only `9,750 if the government did not allow depreciation as a tax-deductible expense. Note that for tax computation, depreciation amount must be calculated as per the Income Tax rules.
We can obtain yet another definition of net cash flows by adjusting Equation (4). Let us add and subtract depreciation (DEP) on the right hand-side of Equation (4):
![]()
and if we use the definition of tax as given in Equation (6), then:

EBIT (1 – T) may also be referred to net operating profit after tax (NOPAT).
Note from Equation (8) that net cash flow from operation is equal to after-tax operating income plus depreciation. In the example, NCF using Equation (9) is given as follows:
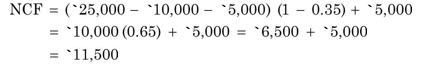
Net Working Capital
In computing net cash flows in the above example, we have assumed that all revenues are received in cash and all expenses are paid in cash. In reality, the actual cash receipts and cash payments will differ from revenues (sales) and expenses as given in the profit and loss account. This difference is caused by changes in working capital items, which include trade debtors (accounts receivable), trade creditors (accounts payable) and stock (inventory). Therefore, Equations (7) and (8) may over-or under-state cash flows. Consider the following situations:
Change in accounts receivable The firm’s customers may delay payment of bills which will increase receivable. Since revenues (sales) include credit sales, it will overstate cash inflow. Thus, increase (or decrease) in receivable should be subtracted from (or added to) revenues for computing actual cash receipts.
Change in inventory The firm may pay cash for materials and production of unsold output. The unsold output increases inventory. Expenses do not include cash payments for unsold inventory, and therefore, expenses understate actual cash payments. Thus, increase (or decrease) in inventory should be added to (or subtracted from) expenses for computing actual cash payments.
Change in accounts payableThe firm may delay payment for materials and production of sold output (sales). This will cause accounts payable (suppliers’ credit) to increase. Since accounts payable is included in expenses, they overstate actual cash payments. Thus, increase (or decrease) in accounts payable should be subtracted from (or added to) expenses for computing actual cash payments.
NCF = EBIT (1 – T ) + DEP – NWC (9)
It is, thus, clear that changes in working capital items should be taken into account while computing net cash inflow from the profit and loss account. Instead of adjusting each item of working capital, we can simply adjust the change in net working capital, viz., the difference between change in current assets (e.g., receivables and inventory) and change in current liabilities (e.g., accounts payable) to profit. Increase in net working capital should be subtracted from and decrease added to after-tax operating profit. Thus, we can extend Equation (8) as follows for computing net cash flow:
where NWC is net working capital.
Free Cash Flows
In addition to an initial cash outlay, an investment project may require some reinvestment of cash flow (for example, replacement investment) for maintaining its revenue-generating ability during its life. As a consequence, net cash flow will be reduced by cash outflow for additional capital expenditures (CAPEX). Thus, net cash flow will be equal to: net operating profit after tax [NOPAT = EBIT (1 – T)] plus depreciation minus (plus) increase (decrease) in net working capital and minus capital expenditure:
![]()
Net cash flows as defined by Equation (10) are called free cash flows (FCFs). These are the cash flows available to service both lenders and shareholders, who have provided, respectively, debt and equity, funds to finance the firm’s investments. Thus, some prefer to call it free cash flows to the firm. It is this cash flow, which should be discounted to find out an investment’s NPV.
Notice the difference between Equations (3) and (10); Equation (10) adjusts profits for taxes and net working capital. Equation (10) provides the most valid definition of free cash flows or net cash flow. Since net cash flows are stated on incremental basis in investment analysis, Equation (10) may be rewritten as follows:*

where (delta) indicates change (increase or decrease).
Equity Cash Flows
What are the cash flows available to equity shareholders? Since equity shareholders are residue owners, cash flows will be adjusted for interest charges and repayment of debt holders’ principal amount (RP). Thus, equity cash flows (ECF) will be:
ECF = (EBIT – INT) (1 – T) + DEP – NWC – CAPEX – RP
= EBIT (1 – T) – INT (1 – T) + DEP – NWC – CAPEX – RP (12)
where INT = interest and RP = repayment of principal. We may notice from Eq. (12) that the effective interest charges are net of the tax shield on the payment of interest (INT – T. INT).
Capital Cash FLows
Capital cash flows (CCF) are the assets cash flows which ignore interest payment, but account for the tax shiled on the interest. Thus, it is net cash flow (free cash flow) plus tax shiled on interest:
CCF = FCF + T. INT
= EBIT (1 – T) + T. INT + DEP – NWC – CAPEX (13)
Terminal Cash Flows
Equation (11) provides a general definition of incremental net cash flow in any period. However, the last or terminal year of an investment may have additional cash flows.
Salvage Value
In the case of a replacement decision, in addition to the salvage value of the new investment at the end of its life, two other salvage values have to be considered: (a) the salvage value of the existing asset now (at the time of replacement decision) and (b) the salvage value of the existing asset at the end of its life, if it were not replaced. If the existing asset is replaced, its salvage value now will increase the current cash inflow, or will decrease the initial cash outlay of the new asset. However, the firm will have to forego its end-of-life salvage value. This means reduced cash inflow in the last year of the new investment.
Salvage value (SV) is the most common example of terminal cash flows. Salvage value may be defined as the market price of an investment at the time of its sale. The cash proceeds net of taxes from the sale of the assets will be treated as cash inflow in the terminal (last) year.
The effects of the salvage values of existing and new assets may be summarized as follows:
Salvage value of the new assetIt will increase cash inflow in the terminal (last) period of the new investment.
Salvage value of the existing asset nowIt will reduce the initial cash outlay of the new asset.
Salvage value of the existing asset at the end of its normal lifeIt will reduce the cash flow of the new investment of the period in which the existing asset is sold.
Sometimes removal costs may have to be incurred to replace an existing asset. Salvage value should be computed after adjusting these costs.
Tax Effect of Salvage Value
A company will incur a book loss if an asset is sold for a price less than the asset’s book (depreciated) value. On the other hand, the company will make a profit if the asset’s salvage value is more than its book value. The profit on the sale of an asset may be divided into ordinary income and capital gain. Capital gain on the sale of an asset is equal to salvage value minus original value of the asset, and ordinary income is equal to original value minus book value (depreciated value) of the asset. Capital gains are generally taxed at a rate lower than the ordinary income. Does a company pay tax on profit or get tax credit on loss on the sale of an asset? In a number of countries, the sale of an asset has tax implications at the time of the sale of the asset. There is some difference in India in this regard. Assets are grouped in the block of assets. The depreciable base of the block of assets is adjusted for the sale of the block asset and no taxes are computed when the asset is sold. This point is illustrated later on in this chapter. However, if an asset does not belong to any block of assets, then, for all practical purposes, the tax on gain or loss is computed at the time of the sale of the asset.
The net salvage value (i.e., net proceeds from the sale of the asset) can be calculated as follows assuming tax implications of the sale of assets:
- SV < BV: Loss
Net proceeds = Salvage value + Tax credit on loss
Net proceeds = SV – T (SV – BV)
- SV > BV but SV < OV: Ordinary Profit
Net proceeds = Salvage value – Tax on profit
Net proceeds = SV – T (SV – BV)
- SV > OV: Ordinary Profit and Capital Gain
Net proceeds = Salvage value – Tax on ordinary profit – Tax on capital gain
Net proceeds = SV – T (OV – BV) – Tc (SV – OV) where SV = salvage value; BV = book (depreciated) value; OV = original value; T = ordinary corporate income tax rate, and Tc = capital gain tax rate.
Besides salvage value, terminal cost flows will also include the release of net working capital. It is reasonable to assume that funds initially tied up in net working capital at the time the investment was undertaken would be released in the last year when the investment is terminated. As discussed earlier, the net working capital in reality may change in every period of the investment’s life. Such changes should be considered in computing annual net cash flows. Increase in net working capital is a cash outflow while decrease in net working capital is a cash inflow. In practice, it may not be possible for a firm to recover the entire net working capital at the end of the project’s life. The actual amount of net working capital recovered should be considered as the cash inflow in the terminal year.
Release of Net Working Capital
Check Your Concepts
- What are three components of cash flows in investments?
- How is depreciation treated in calculating cash flow from operation?
- How do changes in working capital—receivables (debtors), inventory (stock of goods) andpayables (creditors)—affect the computation of cash flow from operation?
- Define free cash flow.
- What does terminal value mean? How is it estimated? How is it accounted for in the cash flowestimation?
CALCULATION OF DEPRECIATION FOR TAX PURPOSES
Two most popular methods of charging depreciation are: straight-line and diminishing balance or written-down value (WDV) methods. For reporting to the shareholders, companies in India could charge depreciation either on the straight-line or the written-down value basis. However, no choice of depreciation method and rates for the tax purposes is available to companies in India. In India, depreciation is allowed as deduction every year on the writtendown value basis in respect of fixed assets as per the rates prescribed in the Income Tax rules. Depreciation is computed on the written down value of the block of assets. Block of assets means a group of assets falling within a class of assets, being buildings, machinery, plant or furniture, in respect of which some percentage of depreciation is prescribed. Oceangoing ships are also included in the block of assets. Assets have been divided into several blocks with different rates of depreciation: for example, 15 per cent, 25 per cent, 50 per cent or 100 per cent. Most of the plants and machineries are covered in the 15 per cent depreciation block. No depreciation is allowed on land.
How is written down value defined? In simple terms, for a single asset, it is the original cost of the asset minus the amount of depreciation charged: OV – DEP. To illustrate, let us consider that an asset of `1,000 which has a three-year life, is acquired on 1 January 20X1. If the prescribed depreciation rate is 25 per cent, the written down value and depreciation of the asset over its life will be as follows:

Depreciation Base
In the case of block of assets, the written down value is calculated as follows:
The aggregate of the written-down value of all assets in the block at the beginning of the year
Minus the proceeds from the sale of any asset in the block during the year (provided such reduction does not exceed the written-down value of the block arrived in the first two items above)Plus the actual cost of any asset in the block acquired during the year
Thus, in a replacement decision, the depreciation base of a new asset (assuming that the new and the old assets belong to the same block of assets) will be equal to: Cost of new equipment + Written-down value of old equipment
– Salvage value of old equipment
How do you estimate cash flows of an investment project? We illustrate the cash flow computations for investment projects, involving the treatment of depreciation and salvage value in the following sections.
Check Your Concepts
- If depreciation is a non-cash expense, why is it considered in the cash flow computation?
- What is the concept of ‘block of assets’ under the Indian tax rules?
- How is the ‘depreciation base’ calculated for an asset which is a replacement for the existingasset in the block of assets?
Cash Flow Estimates for a New Product
| ILLUSTRATION 10.2: Cash Flows for a New Product |
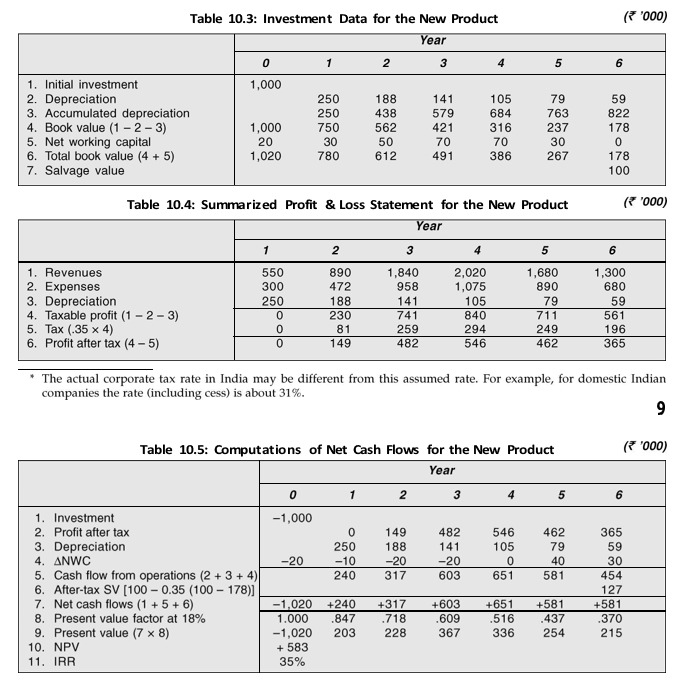
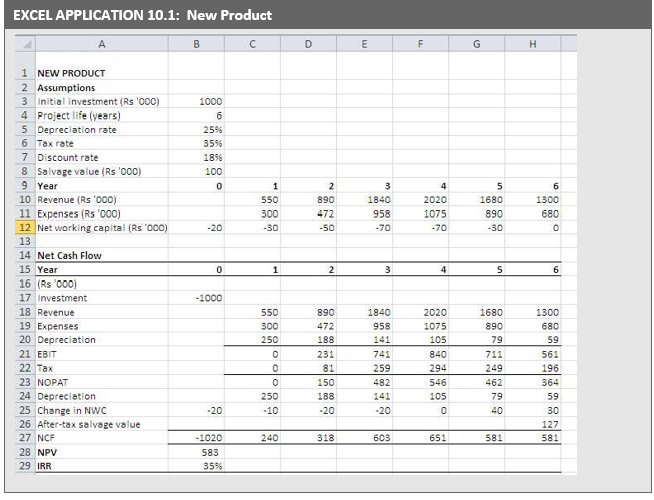
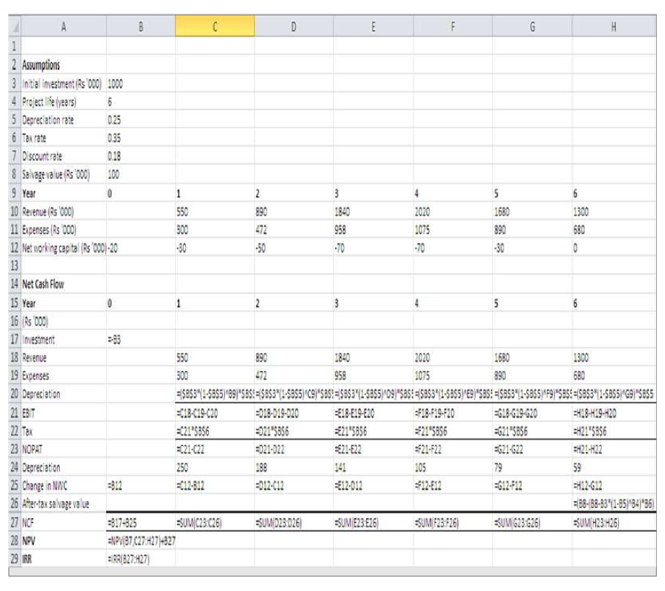
| Bharat Foods Limited is a consumer goods manufacturing company. It is considering a proposal for marketing a new food product. The project will require an investment of `1 million in plant and machinery. It is estimated that the machinery can be sold for `1,00,000 at the end of its economic life of 6 years. Assume that the loss or profit on the sale of the machine is subject to the corporate tax. The company can charge annual written-down depreciation at 25 per cent for the purpose of tax computation. Assume that the company’s tax rate is 35 per cent* and the discount rate is 18 per cent. Table 10.3 gives the initial capital investment, annual depreciation and annual working capital for the project. Notice that the annual written-down value depreciation is calculated as the depreciation rate 25 per cent times the book value at the end of the previous year (which is also book value at the beginning of the current year). Lines 2–4 show computation of depreciation and book value. Line 5 gives the estimates of net working capital, which may be expected to change with sales.
A simplified profit and loss statement for the project is given in Table 10.4. The first step in estimating the project’s cash flows is the forecasts of sales. The marketing executives will have to forecast the units of the product that they could sell as well as the selling price of the product. They will have to keep in mind the competitive pressure and reaction. This makes sales forecasting a tricky job. The estimated sales forecasts in Table 10.4 show that the product demand rises quickly and then starts declining after the fourth year. The estimates of operating expenses and working capital follow the sales forecasts. Table 10.3 and Table 10.4 provide data for determining the project’s net cash flows, which are computed in Table 10.5. |
A new product may be a slight modification of the firm’s existing product or it may be an altogether different, innovative product. The cash flow estimates for a new product will depend on forecasts of sales and operating expenses. Sales forecasts require information on the quantity of sales and the price of the product. The selling price and sales quantity depend on the nature of competition. Anticipating the competitors’ reactions when an innovative product is introduced is not easy. Thus the estimation of cash flows for a new product poses considerable difficulty and challenge. The marketing executives developing sales forecasts should be aware with the forecasting techniques as well as they should have the ability of understanding the dynamics of competition. Hence the cash flow estimation for a new product is both an art and a science. We show in Illustration 10.2 the cash flow pattern for a new product.
Cash Flows From Operations
Cash flows with – (minus) signs are outflows and those with + (plus) signs are inflows. Cash flows from operations (line 5 in Table 10.5) are measured as revenues minus expenses and taxes. It would also be computed as earnings after taxes plus depreciation [EBIT (1 – T ) + DEP]. Note that depreciation is an operating expense for computing taxes, but it is a noncash expense. Therefore, depreciation is added back to profit after taxes to arrive at cash flow from operations. The change in net working capital is yet another item that affects cash flow from operations. Line 5 in Table 10.3 shows the level of working capital to sustain the forecasted sales. Bharat Foods needs upfront working capital investment of `20,000 before it could sell the new product. This is an outflow of cash. The working capital requirement increases by `10,000 in the first year. This is a use of cash. A decrease in working capital will release cash, which means cash inflow. It may be noticed that net working capital increases (outflows) through year 3, but then gets released (inflows) in the last two years. It is assumed that the working capital is recovered without any diminution in value.
After-tax Salvage Value
The machine has a book value of `178,000 and its salvage value is `100,000 at the end of its useful life of 6 years. Hence the book loss on sale of machine is `78,000. Since in this Illustration it is assumed that book loss is subject to corporate tax, the firm will charge loss to its profits and save taxes. Therefore, the after-tax cash proceeds from the sale of machine are `100,000 plus the tax saved; that is: 100,000 – 0.35(100,000 – 178,000) = 100,000 + 27,000 = `127,000.
The net cash flows may be summarized as follows:

We may assume that the project’s risk is similar to the company’s risk. Hence the company’s opportunity cost of capital of 18 per cent is used to discount the project’s cash flows.

The company obtains a net present value of `583,000 when the cash flows are discounted at 18 per cent. Since NPV is positive, the project should be accepted.
How much is the project’s IRR? We can find out the IRR by trial and error. (It is easy to calculate IRR using a computer or a financial calculator.) Let us try 30 per cent discount rate: PV = `1,151 and NPV is `131. We should try a higher rate. Let us try 34 per cent. At 34 per cent: PV is `1,043 and NPV is `23. Since NPV is positive at 34 per cent, let us try 35 per cent. At 35 per cent, PV is `1,018 and NPV is minus `2, which is close to zero. Thus, IRR is approximately 35 per cent. In fact, IRR should be between 34 to 35 per cent. We can find IRR as follows:

Since the project’s IRR is greater than the cut-off rate (the opportunity cost of capital), it should be accepted. Note that a project with positive NPV will have IRR greater than the opportunity cost of capital. The evaluation of the new product is also shown in the Excel Application.
Salvage value and Tax effects
In Illustration 10.2, we assumed that the firm would get tax credit on the book loss (or unrecovered cost) when the machine is sold. In India, as per the current tax laws, the remaining book value (i.e., book value minus salvage value) of an asset, that belongs to a block of assets, is included in the block of assets and therefore, the firm continues availing depreciation deduction on the asset’s unrecovered cost after its sale. This implies that the tax advantage on unrecovered cost via depreciation tax shield would occur over a long period of time (in fact, an infinite period) rather than at the time the asset is sold.
An asset may be sold for more that its book value (written down). This difference, in excess of the asset’s book value, is a book profit on the sale of the asset. According to the Indian tax laws, the balance of the block of assets will reduce by this difference. Hence instead of paying tax on this book profit at the time of sale of the asset, the firm would lose depreciation tax shield in the future. Thus, as per the current tax laws in case of the assets belong to the blocks of assets in India, the after-tax salvage value should be calculated at follows:
Book value (BV or WDV) > Salvage value (SV):
After-tax salvage value = Salvage value + PV of depreciation tax shield on (BV – SV) Salvage value (SV) > Book value (BV):
After-tax salvage value = Salvage value – PV of depreciation tax shield lost on (SV – BV)
In Illustration 10.2, book value is greater than salvage value and the remaining balance of the book value is `78,000. Depreciation on this amount will save tax for the firm forever (infinity). We can use the following formula to calculate the present value of the (perpetually declining annuity) depreciation tax shield after the asset is sold at the end of its useful life:

Note that PVDTSn is the present value of depreciation tax shield at the end of n period, T the tax rate, d the depreciation rate, k the discount rate, BVn is book value at the end of n period and SVn is salvage value at the end of n period. In Illustration 10.2, PV of depreciation tax shield on the remaining book value of `78,000 is:
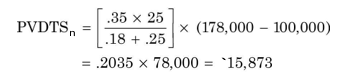
You may notice that this amount is less than the tax saved on book loss allowed at the time of sales of the asset. This is so because the depreciation tax shield occurs over a long period in the future.
Check Your Concepts
- How is the terminal value of a new business calculated?
- How do cash flow estimates of a replacement decision differ from the cash flows of a new asset?
- How will you calculate the differential after-tax salvage value in the case of a replacementdecision?
Cash Flow Estimates for Replacement Decisions
Replacement decisions include decisions to replace the existing assets with new assets. Firms undertake replacement decisions either for cost reduction or quality improvement or both. It is relatively easy to estimate cash flow for replacement decision. Generally, these decisions do not involve sales forecasts. They need an assessment of the possible cost savings or improvement in the quality of product, which, to a large extent, depends on the technical specifications of the equipments. In Illustration 10.3, we show the cash flow calculations for a replacement decision.
| ILLUSTRATION 10.3: Replacement Decision |
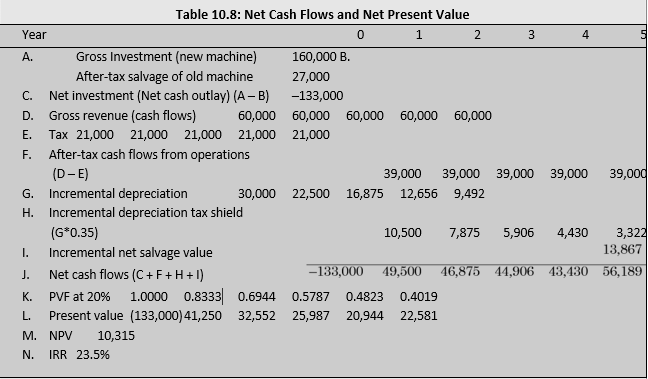
| Excel Engineering Company is considering replacement of one of its existing fabrication machines by a new machine, which is expected to cost `160,000. The existing machine has a book value of `40,000, and can be sold for `20,000 now. It is good for the next 5 years and is estimated to generate annual cash revenues of `200,000 and incur annual cash expenses of `140,000. If sold after 5 years, the salvage value of the existing machine can be expected to be `2,000. The new machine will have a life of 5 years. It is expected to save costs and improve the quality of the product that would help to increase sales. The new machine will yield annual cash revenues of `250,000 and incur annual cash expenses of `130,000. |
| The estimated salvage value of the new machine is `8,000.
Excel Company pays tax at 35 per cent, and can write off depreciation at 25 per cent on the writtendown value of the asset. The company’s opportunity cost of capital is 20 per cent. Should Excel place the existing machine? Assume that there is no inflation. Given the information, we can compute the incremental cash flows of the replacement decision. Table 10.8 shows the computation of net cash flows and net present value. Cash flows with – (minus) signs are outflows and those with + (plus) signs are inflows. The following steps are involved in the computation of net cash flows under two different assumptions about depreciation tax effects: Cash Flow Computation Assuming Tax on Book Profit or Loss on Sale of the Asset We will first assume that the book profit or loss arising from the sale of asset is taxable. The cash flows are calculated as follows. Initial investments The initial investment of the new machine will be adjusted for the after- tax salvage value of the existing machine:
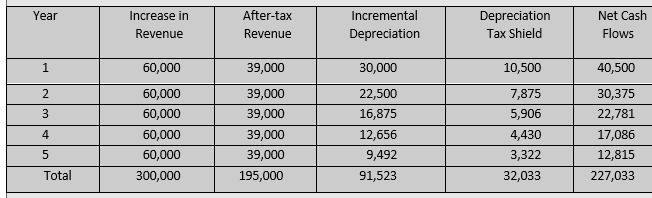
Note that the after-tax salvage value includes salvage value and the tax saved on book loss on the sale of the existing machine. As a result of the sale of the existing machine, the firm will lose depreciation tax benefit on its book value of `40,000. Thus, on incremental (or differential basis) basis, the depreciation tax benefit on the acquisition of the new machine will be computed on `120,000 (viz., `160,000 – `40,000). Thus, there will be tax credit today but the loss of the depreciation tax shield in future on account of the replacement of the new machine. Annual cash flows The annual cash inflows consist of increase in revenue of `50,000 and reduction in costs of `10,000. The net cash flows are calculated by subtracting taxes after considering incremental depreciation as shown in Table 10.7. We can use following formula for calculating net cash flows: NCF = (REV – EXP – DEP)(1 – T) + DEP = (REV – EXP)(1 – T) + T × DEP For example, NCF for year 1 are: NCF = (60,000) (1 – 0.35) + 0.35 × 30,000 = 39,000 + 10,250 = `49,250 Table 10.7: Incremental Cash Flows (`) |
Terminal cash flows The estimated salvage values of the existing machine and new machine respectively are `2,000 and `8,000 after five years. The firm will have to forgo the salvage value of old machine on replacement. Thus, the incremental salvage value is `6,000. Further, the book value on incremental basis after five years is: `120,000 (1 – 0.25)^5 = `28,477. There is estimated book loss of `22,477 on
incremental basis which will save taxes to the firm. Thus, the net (after-tax) salvage value is:
Net salvage value = [SV (new) – {SV (new) – BV (new)} T] – SV (old) – {SV(old) – BV(old)}T
Net salvage value (incremental) = SV (new-old) – {SV(new-old) – BV(new-old)}T
= 6,000 – (6,000 – 28,477) × 0.35 = `13,867
The calculations of incremental net cash flows and net present value is given in Table 10.8.
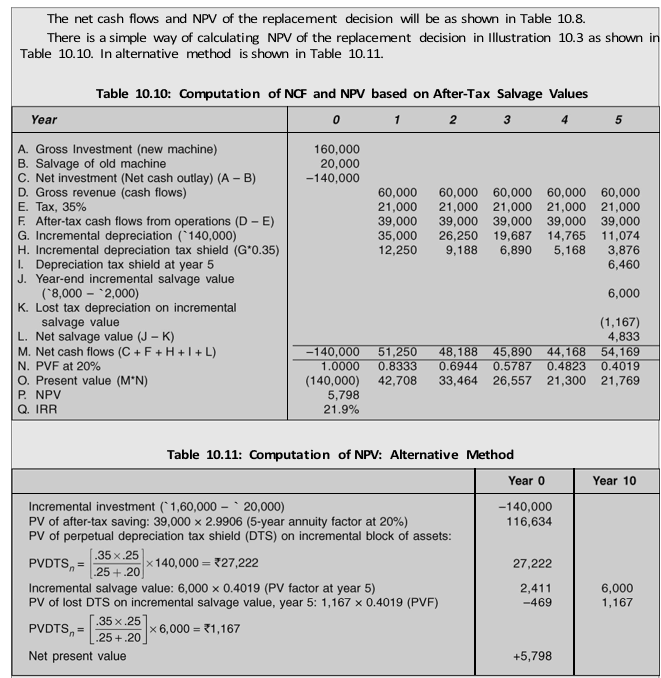
Cash Flow Computations as Per Current Depreciation Rules As stated earlier, as per the current depreciation rules in India, the depreciable base of the block of assets is adjusted when assets are acquired or sold; hence, no computation of tax on sale of an asset is made. In fact, the tax is captured in the depreciation tax shield.
Initial investmentThe initial investment of the new machine will be reduced by the cash proceeds from the sale of the existing machine:

On the acquisition of the new machine and sale of old machine, the incremental gross block will be: `140,000. Notice that taking the incremental gross block as `140,000 fully adjusts for the lost depreciation tax shield (DTS) on the salvage value and that it is not necessary to make any further adjustments while computing the initial outlay.
Annual cash flows from operations The annual cash flows are found on an incremental basis. The new machine will increase gross cash flows by `60,000, which consists of revenues of `50,000 and decrease in expenses of `10,000. Note that the decrease in expenses is an inflow. Net cash flows from operation are found by subtracting payment for taxes after considering incremental depreciation.
Table 10.9 shows the depreciation schedule for the incremental block of assets.
Table 10.9: Depreciation Schedule


ADDITIONAL ASPECTS OF INCREMENTAL CASH FLOW ANALYSIS
The incremental principle should be carefully used in determining an investment’s cash flows. All cash flows occurring because of the investment under consideration should be included. Cash flows, which would occur otherwise, whether or not the project is undertaken, should not be taken into account. Similarly, cash flows, which have occurred before the consideration of an investment, are irrelevant in taking the decision now. The following are the examples of some more aspects of incremental cash flow analysis.
Allocated Overheads
Firms generally have a practice of allocating budgeted general overheads to projects, including the new projects under consideration. Since the general overheads will be incurred whether or not the new projects are undertaken, those allocated overheads should be ignored in computing the net cash flows of an investment. However, some of the overheads may increase because of the new project; these specific to the project should be charged to the project. The incremental cash flow rule indicates that only incremental overheads are relevant.
The allocation of overheads is a difficult question in practice. One or two investment projects may not cause any change in overhead items such as supervision, rent, employees’ welfare or accounting. But the cumulative effect of many investments may ultimately result in an increase in overheads. This creates a problem of cash flow estimation. It is difficult to know when the overheads will change. Efforts should be made to identify such changes so that they may be included in the calculation of net cash flows.
Opportunity Costs of Resources
Incidental Effects
Sometimes a proposed investment project may use the existing resources of the firm for which explicit, or adequate, cash outlays may not exist. The opportunity costs of such projects should be considered. Opportunity costs are the expected benefits, which the company would have derived from those resources if they were not committed to the proposed project. Assume, for example, that a company is considering a project, which requires 7,000 cubic feet of area. Also suppose that the firm has 10,000 cubic feet area available. What is the cost of the area available within the firm if it is used by the project? One answer could be that since no cash outlay is involved, therefore, no charges should be made to the project. But from the point of the alternative investment opportunity foregone by transferring this available area to the project, it seems desirable to charge the opportunity cost of the area to the project. Suppose that the company could rent the area at `18 per cubic foot, and then `1,26,000 should be considered as the opportunity cost of using the area. The opportunity cost of other resources can also be computed in the same manner. It may be sometimes difficult to estimate opportunity cost. If the resources can be sold, its opportunity cost is equal to the market price. It is important to note that the alternative use rule is a corollary of the incremental cash flow rule.
An investment project under consideration may influence the cash flows of other investment opportunities, or the existing projects or products. The incremental cash flow rule applies here; it tells us to identify all cash flows, direct or incidental, occurring as a result of the acceptance of an investment opportunity. It is, therefore, important to note that all incidental effects, in terms of cash flows, should be considered in the evaluation of an investment opportunity. Let us take some examples to illustrate this point.
Contingent Costs
A company is contemplating setting up a chemical plant in a remote, backward area of the state of Gujarat. The company can attract the working force for the plant only if it provides basic facilities such as residential houses, approach roads, schools and hospital to the employees. The estimates of cash flows of the chemical plant would include cash outlay to be incurred in creating these basic facilities for the employees.
Cannibalization
A soft-drink manufacturer is considering the introduction of a new soft-drink, a low-calorie drink. The market research has indicated that the total market for soft drinks would be growing at 10 per cent. The company’s product, ‘Sip-It’, is anticipated to capture 20 per cent of the total soft-drink market. It is also revealed that one-sixth of the total volume of the new product would come from erosion of the company’s one of the existing products, ‘Fresh Cola’, a high-calorie drink. The cash flow estimates of ‘Sip-It’ should include this cannibalization effect, i.e., the lost contribution of the existing product, ‘Fresh Cola.’ Let us add some more information to the present example. The managing director of the soft drink company is not convinced that the sale of ‘Fresh Cola’ will be eroded because of the introduction of the new product, ‘Sip-It.’ His opinion is that if they do not introduce a lowcalorie drink like ‘Sip- It’, competitors would do so; therefore, sale of ‘Fresh Cola’ would be eroded, whether ‘Sip-It’ is introduced or not. If this is a correct information, then the lost contribution of ‘Fresh Cola’ cannot be considered in the evaluation of ‘Sip-It’.
Revenue Enhancement
Consider yet another example. A state government is considering the construction of a railroad bridge. In itself the construction of the bridge may not be beneficial. However, if the incidental effects, such as the operation of railroad, are considered, the proposal may become enormously profitable. The cash flow estimates of constructing the bridge should include the net benefits of operating the railroad. Similarly, a new project may create opportunities for increasing the sale of existing products. Such benefits should be included in the cash flows of the new project.
Sunk Costs
To illustrate, let us assume in our preceding example of the soft drink that before deciding to introduce a new product, the company has conducted a market test. The results of the market test were found to be favourable. Should the company include the market test costs in the evaluation of the new product? The answer is no. The costs of the market test have already been incurred and they are sunk costs; the decision to introduce a new product cannot affect them. They are, therefore, irrelevant to the decision of introducing a new product.
Sunk costs are cash outlays incurred in the past. They are the results of past decisions, and cannot be changed by future decisions. Since they do not influence future decisions, they are irrelevant costs. They are unavoidable and irrecoverable historical costs; they should simply be ignored in the investment analysis.
Consider another example. A company set up a plant for a cost of `200 million to manufacture ball bearings. The project proved to be bad for the company, and it started accumulating losses. The total outflows to-date is `300 million. The company is thinking of abandoning the plant. Some executives consider it suicidal to abandon a plant on which `300 million have already been spent. Others feel it equally unwise to continue with a plant, which has been incurring losses and offers no possibility of any satisfactory return on that money spent. The arguments of both the groups do not make sense. The `300 million spent by the company is a sunk cost; therefore, it is irrelevant. It is also not correct to discard the plant since it is not earning a satisfactory return on a sunken investment. The company should take the decision to sell or not to sell the plant today in light of the future cash flows and return.
Check Your Concepts
- How should ‘allocated’ overheads be treated in an investment evaluation?
- What are sunk costs? Are they relevant in determining a project’s cash flows? Why or why not?
- Give an example of ‘cannibalization’ effect on a project’s cash flows.
Summary
The estimation of cash flows, though difficult, is the most crucial step in investment analysis.
Profits vs cash flows: Cash flows are different from profits. Profit is not necessarily a cash flow; it is the difference between revenue earned and expenses incurred rather than cash received and cash paid. Also, in the calculation of profits, an arbitrary distinction between revenue expenditure and capital expenditure is made.
Incremental cash flows: Cash flows should be estimated on an incremental basis. Incremental cash flows are found out by comparing alternative investment projects. The comparison may simply be between cash flows with and without the investment proposal under consideration when real alternatives do not exist.
Components of cash flows: Three components of cash flows can be identified: (1) initial investment, (2) annual cash flows, and (3) terminal cash flows.
Initial investment: Initial investment will comprise the original cost (including freight and installation charges) of the project, plus any increase in working capital. In the case of replacement decision, the aftertax salvage value of the old asset should also be adjusted to compute the initial investment.
Net cash flow: Annual net cash flow is the difference between cash inflows and cash outflows including taxes. Tax computations are based on accounting profits. Care should be taken in properly adjusting depreciation while computing net cash flows.
Depreciation is a noncash item, but it affects cash flows through tax shield. The following formula can be used to calculate change in net cash flows from operations:
![]()
Working capital and capital expenditure: In practice, changes in working capital items — debtors (receivables), creditors (payable) and stock (inventory) — affect cash flows. Also, the firm may be required to incur capital expenditure during the operation of the investment project. Therefore, the following formula should be used to compute the investment’s net cash flows or free cash flows:
![]()
Free cash flows and the discount rate: Free cash flows are available to service both the shareholders and the debt holders. Therefore, debt flows (interest charges and repayment of principal) are not considered in the computation of free cash flows. The financing effect is captured by the firm’s weighted cost of debt and equity, which is used to discount the project’s cash flows. This approach is based on two assumptions: (1) the project’s risk is the same as the firm’s risk, and (2) the firm’s debt ratio is constant and the project’s debt capacity is the same as the firm’s.
Terminal cash flows are those, which occur in the project’s last year in addition to annual cash flows. They would consist of the aftertax salvage value of the project and working capital released (if any). In case of replacement decision, the foregone salvage value of old asset should also be taken into account.
Terminal value of a new product may depend on the cash flows, which could be generated much beyond the assumed analysis or horizon period. The firm may make a reasonable assumption regarding the cash flow growth rate after the horizon period and use the following formula for calculating terminal value:

The term incremental cash flowsshould be interpreted carefully. The concept should be extended to include the opportunity cost of the existing facilities used by the proposal. Sunk costs and allocated overheads are irrelevant in computing cash flows. Similarly, a new project may cannibalise sales of the existing products.
The project’s cash flows should be adjusted for the reduction in cash flows on account of the cannibalization.
Review Questions
- Distinguish between profits and cash flows. Why are cash flows important in investment decisions?
- What are incremental cash flows? Briefly explain the effects of the following on the calculation ofincremental cash flows: (a) sunk costs, (b) allocated overheads and (c) opportunity costs.
- A company has just tested the market for a new product. The test indicates that the product maycapture about 40 per cent of the market share. It is also expected that 25 per cent of the new product’s share will be at the cost of an existing product. The new product can be manufactured in the existing facilities, which could also be used to meet the expected increase in one of the company’s existing products. The company’s financial analyst argues that she would include the test costs in the new product’s cash flows since they were incurred for testing the new product, but would exclude the lost contribution on an existing product and the value of the existing facilities to be used for the manufacture of the new product because no out-of-pocket cost is incurred. Do you agree with the analyst? Why or why not?
- How should depreciation be treated in capital budgeting? Do the depreciation methods affect thecash flows differently? How?
Quiz Exercises
- A firm wants to replace old equipment, which is capable of generating cash flows of`35,000, `25,000 and `15,000 during the next 3 years. It has a book value of `50,000 and a market value of `15,000. The firm is considering new equipment, which will require an initial cash outlay of `100,000, and is estimated to generate cash flows of `78,000, `70,000 and `45,000 for the next 3 years. Both old and new equipments may be assumed to have a zero resale value after 3 years. The tax rate is zero. Calculate the incremental cash flows.
- A company is considering a proposal for marketing a new product. The project will require aninvestment of `100 million in plant and machinery and it will generate annual cash flows of `64 million. It is estimated that the machinery can be sold for `5 million at the end of its economic life of 7 years. Assume that the loss or profit on the sale of the machine is subject to the corporate tax. The company can charge annual written-down depreciation at 25 per cent for the purpose of tax computation. Assume that the company’s tax rate is 30 per cent and the discount rate is 18 per cent. Should the proposal be accepted?
- A company is considering a proposal of installing new equipment. The equipment would involve acash outlay of `600 million and working capital of `80 million. The expected life of the project is 8 years without any salvage value. Assume that the company is allowed to charge depreciation on straight-line basis for tax purposes, and that the tax rate is 30 per cent. The estimated before-tax cash flows from year 1 through year 8 are: `210 million, `180 million, `160 million, `150 million, `120 million, `100 million, `90 million and `70 million. If the company’s opportunity cost of capital is 12 per cent, calculate the equipment’s net present value and internal rate of return.
- The cash flows of a project from year 0 through year 3 are `65,000 each year. There is a cash outflow of `2,50,000. The firm’s cost of capital is 10 per cent? Should the project be accepted?
- A firm is considering an investment project involving an initial cost of `400 million. The life of the project is estimated as 5 years. The project will provide annual net cash inflow of `160 million. The cost of capital is 15 per cent. Should the project be accepted?
- A company is evaluating a project, which will cost `5,00,000 and will have no salvage value at the end of its 5-year life. The project will save costs of `2,00,000 a year. The company will finance the project by a 12 per cent loan and will repay loan in equal instalments of `1,00,000 a year. The firm’s tax rate is 30 per cent and the after-tax cost of capital is 15 per cent. What is the NPV of the project? Assume straight-line depreciation for tax purposes.
- A firm has a beta of 1.45. The risk-free rate is 9 per cent and the market risk premium is 10 per cent.The firm’s cost of borrowings is 12 per cent and it maintains a target debt-equity ratio of 1.5 : 1. The tax rate is 30 per cent. Calculate the firm’s weighted average cost of capital. What is the firm’s real cost of capital if inflation rate is 5 per cent?
