Introduction
Firms are exposed to interest rate movements in two ways:
- The cost of existing borrowings (or the yield on deposits) may be linked to interest rates in the economy. This risk exposure can be eliminated by using fixed rate products.
- Cash flow forecasts may indicate the need for future borrowings/deposits. Interest rates may change before these are needed and thus affect the ultimate cost/yield.
- The second type of risk is the focus of this chapter.
More explanation of interest rate risk
Interest rate risk exposure
Interest rate risk is the risk of incurring losses due to adverse movements in interest rates. An exposure to interest rate risk arises in the following situations.
- An organisation is expecting some income in the future, and the amount of income received will depend on the interest rate at that time.
- An organisation is expecting to make some payment in the future, and the amount of the payment will depend on the interest rate at the time.
- The organisation has an asset whose market value changes whenever market interest rates change.
The greatest exposures to interest rate risk are faced by banks and investment institutions. However, non -bank companies can also have substantial exposures to interest rate risk.
- Many companies borrow at a floating rate of interest (or variable rate of interest).
- For example, a company might borrow at a variable rate of interest, with interest payable every six months and the amount of the interest charged each time varying according to whether short-term interest rates have risen or fallen since the previous payment.
- Some companies also budget to receive large amounts of cash, and so budget large temporary cash surpluses that can be invested short-term. Income from those temporary investments will depend on what the interest rate happens to be when the money is available for depositing. Some investments earn interest at a variable rate of interest (for example money in bank deposit accounts) and some short-term investments go up or down in value with changes in interest rates (for example, Treasury bills and other bills).
- Some companies hold investments in marketable bonds, either government bonds or corporate bonds. These change in value with movements in long-term interest rates.
- Some companies borrow by issuing bonds. If a company foresees a future requirement to borrow by issuing bonds, it will have an exposure to interest rate risk until the bonds are eventually issued.
- Many companies borrow, and if they do they have to choose between borrowing at a fixed rate of interest (usually by issuing bonds) or borrow at a floating rate (possibly through bank loans). There is some risk in deciding the balance or mix between floating rate and fixed rate debt. Too much fixed rate debt creates an exposure to falling long-term interest rates and too much floating rate debt creates an exposure to a rise in short-term interest rates.
Interest rate risk can be significant. For example, suppose that a company wants to borrow $10 million for one year, but does not need the money for another three weeks. It would be expensive to borrow money before it is needed, because there will be an interest cost. On the other hand, a rise in interest rates in the time before the money is actually borrowed could also add to interest costs. For example, a rise of just 0.25% (25 basis points) in the interest rate on a one-year loan of $10 million would cost an extra $25,000 in interest.
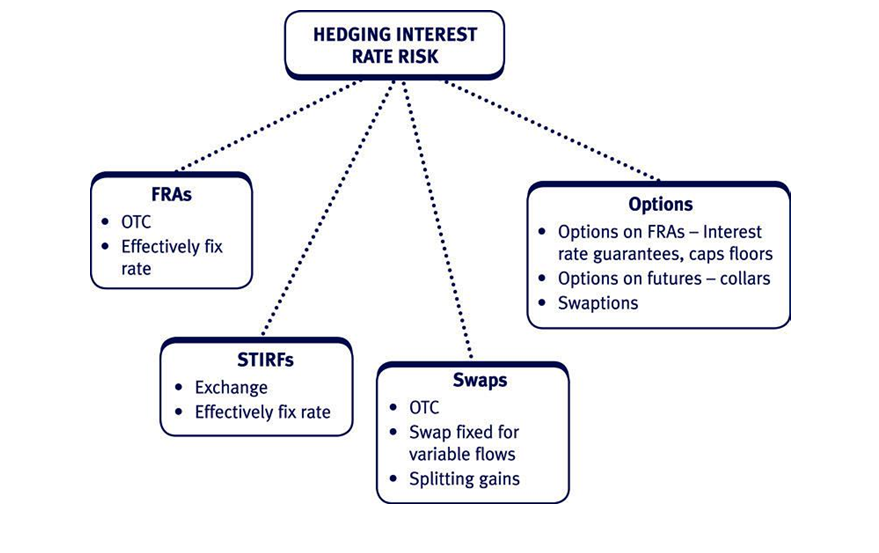
Forward rate agreements (FRAs)
Introduction
- Using an FRA effectively fixes the rate of interest on a loan or deposit.
- In the terminology of the markets, an FRA for a three-month loan/deposit starting in five months’ time is called a ‘5–8 FRA’ (or ‘5v8 FRA’).
- Two rates are usually quoted, the higher one for borrowing and the lower one for investing.
More detail on FRAs
Hedging using FRAs
Hedging is achieved by a combination of an FRA with the ‘normal’ loan or deposit.
When an FRA reaches its settlement date (usually the start of the notional loan or deposit period), the buyer and seller must settle the contract:
Borrowing (hence concerned about interest rate rises)
- The firm will borrow the required sum on the target date and will thus contract at the market interest rate on that date.
- Separately the firm will buy a matching FRA from a bank or other market maker and thus receive compensation if rates rise.
Depositing (hence concerned about a fall in interest rates)
- The firm will deposit the required sum on the target date and will thus contract at the market interest rate on that date.
- Separately the firm will sell a matching FRA to a bank or other market maker and thus receive compensation if rates fall.
In each case this combination effectively fixes the rate.
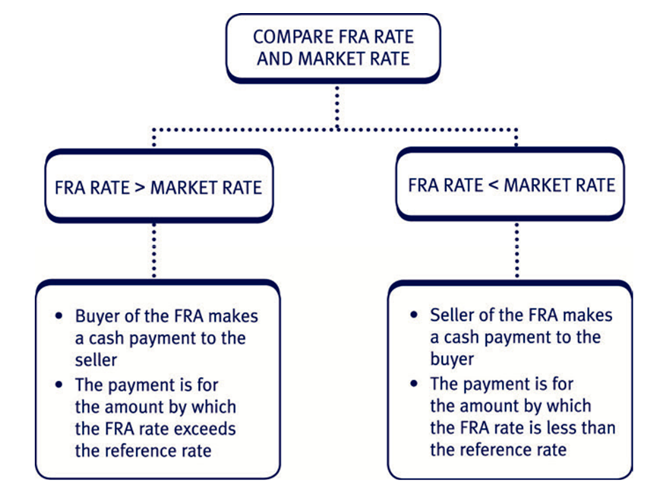
Illustration 1 – FRA
It is now the 1st November 20X6. Enfield Inc’s financial projections show an expected cash deficit in two months’ time of $8m, which will last for approximately three months. The treasurer is concerned that interest rates may rise before the 1st January 20X7, so he is considering using an FRA to fix the interest rate.
The bank offers a 2 – 5 FRA at 5.00% – 4.70%.
Required:
Calculate the interest payable if in two months’ time the market rate is: (a) 7% or (b) 4%.
Solution
The rate for borrowing is 5% – the higher of the two rates quoted.
| Loan payments | 7% | 4% | |
| Interest payable on loan: 8m × 0.07 × 3/12 | = | (140,000) | |
| 8m × 0.04 × 3/12 | = | (80,000) |
FRA payments
Compensation:
Receivable 8m × (0.07 – 0.05) × 3/12 = 40,000
Payable 8m × (0.04 – 0.05) × 3/12 = (20,000)
––––––– –––––––
Combination gives an effective
interest rate of 5%. (100,000) (100,000)
––––––– –––––––
- In this case the company is protected from a rise in interest rates but is not able to benefit from a fall in interest rates – a FRA hedges the company against both an adverse movement and a favourable movement.
- The FRA is a totally separate contractual agreement from the loan itself and could be arranged with a completely different bank.
- FRAs are usually on amounts > $1m and enable you to hedge for a period of one month up to two years. However, as an ‘over the counter’ instrument, they can be tailor-made to the company’s precise requirements.
Settlement payment on an FRA
Because the settlement payment is made at the start of the loan/deposit period, the actual payment made is the present value of the interest differential at that date, discounted using the market reference interest rate.
Illustration
Using the details for the Enfield Inc example above with a 7% market rate:
- The difference in interest rates gave rise to a potential receipt of $40,000 from the bank.
- The actual amount received will be 40,000/(1 + 0.07 × 3/12) = $39,312.
- One approach is to use this to reduce the loan from $8 million to $7,960,688. If this sum is then borrowed at 7% for 3 months, then the final repayment will be:
7,960,688 × (1 + 0.07 × 3/12) = 8,100,000
This gives an effective interest rate of $100,000 on $8m, or 5%.
How does the bank set the interest rate for an FRA?
FRA rates are set by the bank by analysing the individual company’s spot yield curve (introduced in the earlier chapter on the weighted average cost of capital).
Illustration 2
Stone Co’s yield curve has been calculated as:
| Year | Individual yield curve (%) |
| 1 | 3.96 |
| 2 | 4.25 |
| 3 | 4.56 |
This means that Stone Co will have to pay interest of 3.96% if it wants to borrow money for 1 year, 4.25% if it wants to borrow for 2 years etc.
An alternative to borrowing for 2 years at 4.25% throughout is to borrow for 1 year initially at 3.96% and then to borrow for another year in 1 year’s time at an unknown rate. The company could fix the interest rate in one year’s time by asking the bank to quote a rate for a12 – 24 FRA.
The rate quoted by the bank would be the rate r, so that:
1.0396 × (1 + r) = 1.04252
Rearranging this gives r = 4.54%.
Hence the 12 – 24 FRA rate for Stone Co would be 4.54%.
Test your understanding 1
Stone Co (the company in the previous Illustration) wants to borrow money in 2 years’ time for a period of 1 year.
Required:
Using the company’s spot yield information quoted above, calculate the rate of interest the bank would quote for a 24 – 36 FRA.
Student Accountant article
The examiner’s article ‘Determining interest rate forwards… ‘ in the Technical Articles section of the ACCA website covers the calculation of FRA rates in more detail.
3 Options on FRAs
Interest rate guarantees (options on FRAs)
- An interest rate guarantee (IRG) is an option on an FRA and, like all options, protects the company from adverse movements and allows it take advantage of favourable movements.
- If borrowing money, a firm would buy an FRA (explained above), so a call option over FRAs would be used. Similarly a put option over FRAs would be used to cover a deposit.
- IRGs are usually written by banks and other financial houses (i.e. the same organisations that may offer FRAs).

- IRGs are more expensive than the FRAs as one has to pay for the flexibility to be able to take advantage of a favourable movement.
Illustration 3 – IRG
Harry Inc wishes to borrow $8m in two months’ time for a period of three months.
An IRG is available at 5% for a premium of 0.1% of the size of the loan.
Required:
Calculate the interest payable if in two months’ time the market rate is: (a) 7% or (b) 4%.
Solution
7% – 4% – allow
exercise to lapse
Interest 8m × 3/12 × 5% (100,000)
8m × 3/12 × 4% (80,000)
Premium = Cost of option (8,000) (8,000)
–––––––– –––––––
Total payment (108,000) (88,000)
–––––––– –––––––
Note: There is no need to time apportion the premium percentage.
Test your understanding 2
RGI Co wishes to invest $12 million in 6 months’ time for two months and considering the following hedging strategies.
- A 6 – 8 FRA quoted at 4%.
- An IRG at 4% for a premium of 0.1%.
Required:
Determine the costs if in six months’ time the market rate is: (a) 5% (b) 3% and comment.
When to hedge using FRAs or IRGs
- If the company treasurer believes that interest rates will rise, will he use an FRA or an IRG? He will use an FRA, as it is the cheaper way to hedge against the potential adverse movement.
- If the treasurer is unsure which way interest rates will move he may be willing to use the more expensive IRG to be able to benefit from a potential fall in interest rates.
4 Interest rate futures (IRFs)
Introduction
An interest rate futures contract fixes the interest rate on a future loan or deposit.
More details on interest rate futures
Types of IRFs
There are two broad types of interest rate futures:
- Short-term interest rate futures (STIRs). These are standardised exchange-traded forward contracts on a notional deposit (usually a three-month deposit) of a standard amount of principal, starting on the contract’s final settlement date.
- Bond futures. These are contracts on a standard quantity of notional government bonds. If they reach final settlement date, and a buyer or seller does not close his position before then, the contracts must be settled by physical delivery.
Futures hedging calculations
Step 1: Set up the hedge by addressing 3 key questions:
- Do we initially buy or sell futures?
- How many contracts?
- Which expiry date should be chosen?
Step 2: Contact the exchange. Pay the initial margin. Then wait until the transaction/settlement date.
Step 3: Calculate profit or loss in the futures market by closing out the futures contracts, and calculate the value of the transaction using the market rate of interest rate on the transaction date.
Calculations – Particular characteristics of IRFs
Underlying assets
To understand whether you need to buy or sell contracts, interest rate futures are best understood as involving the sale or purchase of bonds.
- borrowing money equates to issuing (selling) bonds, so sell futures to set up the hedge.
- depositing funds equates to buying bonds, so buy futures to set up the hedge.
Futures prices
- Interest rate futures prices are stated as (100 – the expected market reference rate), so a price of 95.5 would imply an interest rate of 4.5%.
- Open and settlement prices – in an exam question, when setting up the hedge, you may be quoted ‘Open’ and ‘Settlement’ futures prices. When setting up the hedge, the ‘Settlement’ price should be used – the ‘Open’ price is not relevant in our calculations.
Calculating the number of contracts needed
| Number of contracts = | Loan or deposit amount | × | Loan or deposit period in months | |
| Contract size | Contract duration | |||
More practical information on IRFs
Contract specifications
Short-term interest rate futures are traded on a number of futures exchanges. For example:
- STIRs for sterling (three-month LIBOR) and the euro (three-month euribor) are traded on LIFFE, the London futures exchange.
- A STIR contract for the US dollar (eurodollar) is traded on the Chicago Mercantile Exchange (CME).
Here are just a few STIR contract specifications.
Short-term interest rate futures
| Reference rate | Futures exchange | Notional deposit |
| 3-month sterling | LIFFE | £500,000 |
| 3-month euribor | LIFFE/Eurex | €1 million |
| 3-month eurodollar | CME | $1 million |
| 3-month euroyen | TFE/LIFFE | ¥100 million |
Ticks and tick values
- For STIRs, the minimum price movement is usually 0.01% or one basis point. The value of a tick is calculated as follows:
– Tick value = unit of trading (i.e. amount of principal) × one basis point × fraction of year.
– For three-month sterling (‘short sterling’) futures, the underlying deposit for one contract is £500,000, so the value of one tick is £500,000 × 0.0001 × 3/12 = £12.50.
– For three-month euribor futures, the underlying deposit is €1,000,000, so the value of one tick is €1,000,000 × 3/12 × 0.0001 = €25.
– For three-month eurodollar futures, the underlying deposit is $1,000,000, so the value of one tick is $1,000,000 × 3/12 × 0.0001 = $25.
Note: For three -month euroyen futures, the underlying deposit is ¥100 m but the tick size is 0.005%, so the value of one tick is ¥100 million × 3/12 × 0.00005 = ¥1250.
Illustration of an interest rate futures calculation
Global Inc wishes to borrow €9,000,000 for one month starting in
5 weeks’ time. Euribor is currently 3% and the treasurer of Global decides to fix the rate by selling interest rate futures at 96.90. The market rate subsequently rises by 25 basis points to 3.25%. As soon as the loan is agreed, the treasurer closes out Global’s position by buying a matching number of contracts at 96.65.
Required:
- Calculate the number of contracts required (Note: One 3-month contract is for €1,000,000).
- Demonstrate that, in this case, the gain on the futures contracts exactly matches the extra interest on the loan.
Solution
- Number of contracts = (9,000,000/1,000,000) × 1/3 = 3
- Extra interest cost on loan = 0.25% × 9,000,000 × 1/12 = €1,875
Gain on futures = 3 contracts × 25 ticks per contract × €25 per tick (W) = €1,875
(W: Value of tick = €1,000,000 × 3/12 × 0.0001 = €25)
Test your understanding 3
Assume that today is the 25th of January.
A company is going to borrow $2,000,000 in two months’ time for a period of three months. It fears that the current interest rate will rise from its current level of 5%, so it wants to use $500,000 3-month interest rate futures to hedge the position.
Data from the futures market:
March futures price = 94.90
June futures price = 94.65
Required:
Calculate the result of the relevant futures hedge on the assumption that interest rates have risen to 7% and the futures price has moved to 92.90 in two months’ time.
Basis in interest rate futures
In the previous chapter, we saw that basis for a currency futures contract was defined as:
Spot rate – futures price.
For an interest rate futures contract, because of the way the contract price is quoted as (100-expected interest rate) the calculation is slightly different. Basis in an interest rate futures contract is calculated as:
(100 – Spot rate of interest (e.g. the current LIBOR rate)) – futures price.
Therefore, if the current LIBOR rate is 5.00% and the futures price is 95.50, the basis is:
(100 – 5.00) – 95.50 = – 0.50%
The futures ‘lock-in rate’
As with currency futures, we can use this basis value, together with the assumption that basis reduces steadily to zero over the period before the expiry date of the contract, to predict closing futures prices and the likely futures ‘lock-in rate’.
With interest rate futures, the lock-in rate is calculated as:
100 – (current futures price + unexpired basis on the transaction date).
Test your understanding 4
Sopoph Co is using June interest rate futures to cover the interest rate risk on a 3 month $1 m borrowing starting on 31 May.
At the time the $500,000 futures contracts are set up on 1 January, the LIBOR rate is 5.00% and the futures price is 95.48. Sopoph Co can borrow at the LIBOR rate.
Assume that basis reduces in a linear manner.
Required:
- Calculate the financial result of the futures hedge on the assumption that the LIBOR rate on 31 May is 4.00%.
- Calculate the likely lock-in rate for this futures hedge, and hence the likely financial result of the hedge.
- Comment on your results to parts (a) and (b).
5 Options on interest rate futures
Options on futures
- Traded options are options to buy or sell futures.
- A call option gives the holder the right to buy the futures contract.
- A put option gives the holder the right to sell the futures contract.
- You always buy the option – buy the right to buy or buy the right to sell.
Exercise prices and premium costs
- When you are setting up the hedge position for an option you have a number of prices (exercise prices) from which to choose (as opposed to the futures position where you buy or sell at the current price).
Option prices
LIFFE option price on three-month Sterling December futures.
| Exercise price | Premium | ||
| Calls | Puts | ||
| 93.50 | 2.20 | 1.25 | |
| 94.00 | 1.74 | 1.84 | |
| 94.50 | 1.32 | 2.90 | |
| 95.00 | 0.87 | 3.46 | |
- If a company had a deposit of £500,000 and the treasurer wanted to hedge the position using traded options, he would buy a call option. If he purchased it at an exercise price of 95.00 he would be buying the right to interest receipts at 5% this would cost him a premium 0.87% (i.e. 0.87% × 100) 87 ticks (i.e. 87 × £12.50) = £1,088 per contract.
- If he purchased it at 93.50 he would be buying the right to interest receipts at 6.50% this would cost him a premium 2.20% (i.e. 2.20% × 100) 220 ticks (i.e. 220 × £12.50) = £2,750 per contract.
The premium cost of the option will obviously depend on the exercise price chosen. Buying a call option at 93.50 should be more expensive than buying at 95.00, as the company has a greater chance of a profit when it comes to closing out its futures position.
Choosing an exercise price
There are various ways of choosing an exercise price.
- NB: In a question, you may be told which exercise price to use, so check that first.
- One common way is to choose the exercise price closest to the current interest rate, so if the current interest rate were 6.00% then an exercise price of 94.00 would be chosen.
- Alternatively, choose the exercise price that will result in the highest net interest receipt or minimum total interest payment.
Choosing an exercise price
CALL OPTIONS – deposit – highest net receipt.
| Exercise price | Deposit interest | Cost | Net receipt |
| % | % | % | |
| 93.50 | 6.50 | (2.20) | 4.30 |
| 94.00 | 6.00 | (1.74) | 4.26 |
| 94.50 | 5.50 | (1.32) | 4.18 |
| 95.00 | 5.00 | (0.87) | 4.13 |
PUT OPTIONS – loan – lowest total payment.
| Exercise price | Loan interest | Cost | Total payment |
| % | % | % | |
| 93.50 | 6.50 | 1.25 | 7.75 |
| 94.00 | 6.00 | 1.84 | 7.84 |
| 94.50 | 5.50 | 2.90 | 8.40 |
| 95.00 | 5.00 | 3.46 | 8.46 |
Options hedging calculations
Step 1: Set up the hedge by addressing 4 key questions:
- Do we need call or put options?
- How many contracts?
- Which expiry date should be chosen?
- Which strike price/exercise price should be used?
Step 2: Contact the exchange. Pay the upfront premium. Then wait until the transaction/settlement date.
Step 3: On the transaction date, compare the option price with the prevailing market interest rate to determine whether the option should be exercised or allowed to lapse.
Step 4: Calculate the net cash flows – beware that if the number of contracts needed rounding, there will be some borrowing or deposit at the prevailing market interest rate even if the option is exercised.
Decision point – Exercise the option or allow it to lapse
General rule:

Double check:
- Would you ever exercise an option that results in a loss?
- Therefore you must always have a profit on the futures when exercising and a potential loss if you allow the option to lapse.
Test your understanding 5 – Interest rate options It is now the 31st of July.
Tolhurst Co needs to borrow $10m in 1 month’s time, for a 6 month period. The current market interest rate is 5%.
The following information is available regarding $500,000 3-month
September interest rate options:
| Exercise price | Call | Put |
| 94.50 | 1.39 | – |
| 94.75 | 1.02 | 0.18 |
| 95.00 | 0.65 | 0.65 |
| 95.25 | 0.21 | 1.12 |
| Premia are quoted in %. |
Required:
Calculate the result of the options hedge if the interest rate has risen to 7.5% and if the September futures price has moved to 93.00 in one month’s time.
Comparison of options and futures
Note that interest rate options over futures contracts behave in exactly the same way as futures contracts if we decide to exercise. So, for example with a call option, if we exercise we buy futures at the option exercise price before selling at the ‘normal’ futures price on the transaction date.
If the closing futures price is not given, it might have to be calculated by estimating the amount of unexpired basis on the transaction date as detailed above in the examples on futures contracts.
Student Accountant article
The article ‘Interest rate risk management’ in the Technical Articles section of the ACCA website provides a detailed example of how to answer an exam question on interest rate futures and options.
Test your understanding 6 – Futures and options
Chesterfield Co needs to borrow $5m for 6 months, starting in 4 months’ time on 1st August.
The current LIBOR rate is 3.50% but there is a risk that interest rates will change over the next few months by up to 0.5% either way, so the company’s treasurer is considering hedging the interest payments using futures contracts or options. Chesterfield Co can borrow at 25 basis points above the LIBOR rate.
Current futures/options information:
Futures ($500,000 3 month contracts)
June 96.40
September 96.10
December 95.86
Options on futures (premia quoted as an annual percentage)
| Exercise price | Calls | Puts | ||||
| June | Sept | Dec | June | Sept | Dec | |
| 96.40 | 0.155 | 0.260 | 0.320 | 0.305 | 0.360 | 0.445 |
Required:
Estimate the likely financial position if Chesterfield Co hedges the interest rate risk using:
- futures contracts
- options over futures contracts.
and recommend which method the company should use in this case.
Caps, floors and collars
Options terminology – Caps and floors
Caps
We have seen above that a borrower will hedge against the risk of interest rate rises by buying a put option over interest rate futures.
A cap is another name for this put option over interest rate futures.
Floors
Similarly, a depositor will hedge against the risk of interest rate falls by buying a call option over interest rate futures.
Such an option can also be called a floor.
Options terminology – Collars
- A company buys an option to protect against an adverse movement whilst allowing it to take advantage of a favourable movement in interest rates. The option will be more expensive than a futures hedge. The company must pay for the flexibility to take advantage of a favourable movement.
- A collar is a way of achieving some flexibility at a lower cost than a straight option.
- Under a collar arrangement the company limits its ability to take advantage of a favourable movement.
- For example, for a borrower, it buys a cap (a put option) as normal but also sells a floor (a call option) on the same futures contract, but with a different exercise price.
- The floor sets a minimum cost for the company. The counterparty is willing to pay the company for this guarantee of a minimum income. Thus the company gets paid for limiting its ability to take advance of a favourable movement if the interest rate falls below the floor rate the company does not benefit therefore the counterparty does.
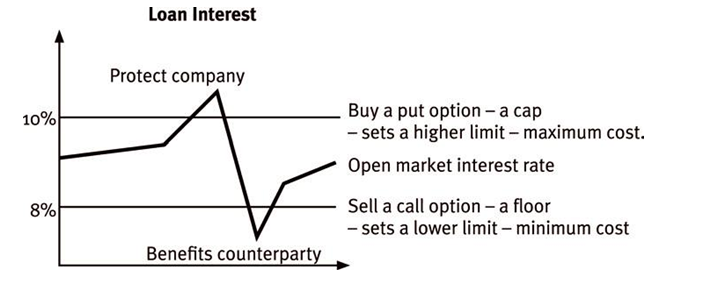
- It involves a company arranging both a minimum and a maximum limit on its interest rates payments or receipts. It enables a company to convert a floating rate of interest into a semi-fixed rate of interest.
Test your understanding 7
A company wishes to borrow $10m on the 1st of March for three months. The company can borrow at LIBOR + a fixed margin of 2%. LIBOR is currently 8%.
It is keen to hedge using options, to prevent an increase in LIBOR rate causing the borrowing rate to rise above the existing level. However, having made initial enquiries, it has been discouraged by the cost of the option premium.
A member of its treasury team has suggested the use of a collar to reduce the premium cost of the purchased option.
| Market data: Interest rate options | ||||
| CALLS | PUTS | |||
| Exercise price | March | June | March | June |
| 92.00 | 0.80 | 0.77 | 0.20 | 0.22 |
| 93.00 | 0.15 | 0.12 | 0.60 | 0.70 |
Required:
Calculate the effective interest rate the company will pay using a collar if:
- LIBOR rises to 9.5% and futures prices move to 90.20.
- LIBOR falls to 4.5% and futures prices move to 96.10.
Interest rate swaps
Introduction
An interest rate swap is an agreement whereby the parties agree to swap a floating stream of interest payments for a fixed stream of interest payments and via versa. There is no exchange of principal:
- The companies involved are termed ‘counter-parties’.
- Swaps can run for up to 30 years.
- Swaps can be used to hedge against an adverse movement in interest rates. Say a company has a $200m floating loan and the treasurer believes that interest rates are likely to rise over the next five years. He could enter into a five-year swap with a counter party to swap into a fixed rate of interest for the next five years. From year six onwards, the company will once again pay a floating rate of interest.
- A swap can be used to obtain cheaper finance. A swap should result in a company being able to borrow what they want at a better rate under a swap arrangement, than borrowing it directly themselves.
Calculations based on splitting gains
- The precise details of the swap arrangement will depend on how the potential gains are split between the two counter-parties.
Illustration 4 – Interest rate swap
Company A wishes to raise $10m and to pay interest at a floating rate, as it would like to be able to take advantage of any fall in interest rates. It can borrow for one year at a fixed rate of 10% or at a floating rate of 1% above LIBOR.
Company B also wishes to raise $10m. They would prefer to issue fixed rate debt because they want certainty about their future interest payments, but can only borrow for one year at 13% fixed or LIBOR + 2% floating, as it has a lower credit rating than company A.
Required:
Calculate the effective swap rate for each company – assume savings are split equally.
Solution
Step 1: Identify the type of loan with the biggest difference in rates.
- Answer: Fixed
Step 2: Identify the party that can borrow this type of loan the cheapest.
- Answer: Company A
- Thus Company A should borrow fixed, company B variable, reflecting their comparative advantages.
Step 3:
- Company A has cheaper borrowing in both fixed and variable. Interest rate differentials are 3% for fixed and 1% for variable. The difference between these (2%) is the potential gain from the swap.
- Splitting this equally between the two counter parties, each should gain by 1%.
One way (there are many!) of achieving this is for A to pay B LIBOR (variable) and for B to pay A 10%.
Summary
A
B
Actual borrowing
(10%)
(LIBOR + 2%)
A to B
(LIBOR)
LIBOR
B to A
10%
(10%)
| Interest rates after swap | (LIBOR) | (12%) |
| Open market cost – no swap | (LIBOR + 1%) | (13%) |
| Saving | 1% | 1% |
Test your understanding 8
Company X wishes to raise $50m. They would prefer to issue fixed rate debt and can borrow for one year at 6% fixed or LIBOR + 80 points.
Company Y also wishes to raise $50m and to pay interest at a floating rate. It can borrow for one year at a fixed rate of 5% or at LIBOR +
Required:
Calculate the effective swap rate for each company – assume savings are split equally.
Calculations involving quoted rates from intermediaries
In practice a bank normally arranges the swap and will quote the following:
- The ‘ask rate’ at which the bank is willing to receive a fixed interest cash flow stream in exchange for paying LIBOR.
- The ‘bid rate’ that they are willing to pay in exchange for receiving LIBOR.
- The difference between these gives the bank’s profit margin and is usually at least 2 basis points.
Note: LIBOR is the most widely used benchmark or reference rate for short-term interest rates worldwide, although the swap could relate to Euribor, say.
Illustration 5 – Interest rate swap via an intermediary
Co A currently has a 12 -month loan at a fixed rate of 5% but would like to swap to variable. It can currently borrow at a variable rate of LIBOR + 12 basis points.
The bank is currently quoting 12-month swap rates of 4.90 (bid) and 4.95 (ask).
Required:
Show Co A’s financial position if it enters the swap.
Solution
Co A
Actual borrowing (5.00%)
Payment to bank (LIBOR)
Receipt from bank (bid) 4.90%
––––––––––––––
Net interest rate after swap (LIBOR + 0.10%)
––––––––––––––
Open market cost – no swap (LIBOR + 0.12%)
Saving 2 basis points
Further swap example
Company A has a 12 month loan at a variable rate of LIBOR + 50 basis points but, due to fears over interest rate rises, would like to swap to a fixed rate. It can currently borrow at 5.40% fixed.
Company B currently has a 12 month loan at a fixed rate of 4.85% but would like to swap to variable. It can currently borrow at a variable rate of LIBOR + 65 basis points.
The bank is currently quoting 12 month swap rates of 4.50 (bid) and 4.52 (ask).
Required:
Show how the swap via the intermediary would work.
Solution
- Co A already has a variable outflow so must receive LIBOR from the bank to convert this to fixed. It will pay the bank the ask rate.
- Similarly Co B must pay the bank variable and receive fixed at the bid rate.
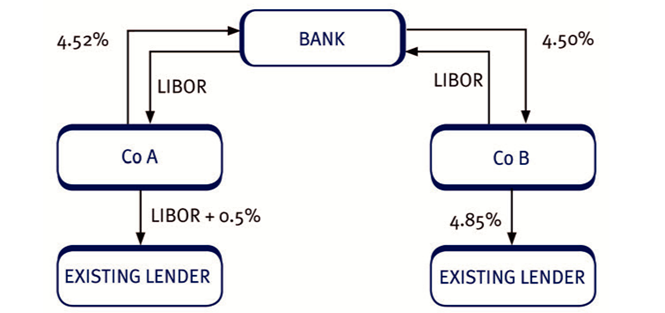
| Actual borrowing | (LIBOR + 0.5%) | (4.85%) |
| Payment to bank | (4.52%) | (LIBOR) |
| Receipt from bank | LIBOR | 4.50% |
| ––––––––––––– | ––––––––––––– |
| Net interest rates after swap | (5.02%) | (LIBOR + 0.35%) |
| ––––––––––––– | ––––––––––––– | |
| Open market cost – no swap | (5.40%) | (LIBOR + 0.65%) |
| Saving | 38 basis points | 30 basis points |
Note: In this case A can borrow variable cheaper but B can get the best fixed rates. In this case the total potential saving = D fixed + D variable = 55 + 15 = 70 basis points.
Of this, 2 basis points have gone to the bank via the spread in quoted prices, leaving 68 to be shared between the two companies.
Using the yield curve and FRA rates to set swap rates
In the examples of swap agreements above, the bank agreed to pay a fixed stream of payments to a company in exchange for a variable stream of payments made by the company to the bank (or vice versa).
The bank decides what the fixed payment should be by analysing the company’s yield curve.
The key consideration is that at the inception of the swap:
PV of the variable rate payments = PV of the fixed rate payments when both are discounted at the spot yield.
Notice how, in the Illustration below, the calculated swap rate payments are based on the forward interest rates/FRA rates (calculated earlier in this chapter). This is because the forward rates are our best estimate of what the actual interest rates might be in the future.
Numerical illustration
Stone Co has $10m of debt finance, and it pays interest at a variable rate based on its current yield curve rates of:
| Year | Individual yield curve (%) |
| 1 | 3.96 |
| 2 | 4.25 |
| 3 | 4.56 |
There is a likelihood that interest rates will rise over the next few months, so the Stone Co financial manager has asked the bank to arrange a three year swap, where Stone Co will pay a fixed annual rate to the bank, in exchange for a variable rate based on the given yield curve rate less 30 basis points.
Required:
Assuming that Stone Co will receive a variable rate based on the given yield curve rate less 30 basis points from the bank, calculate the fixed rate of interest which Stone Co will have to pay to the bank in the swap.
Solution
The bank’s variable payments under the swap agreement (based on the current yield curve rates) will be:
Year %
- 96 – 0.30 = 3.66%, or $366k on $10m
- 54 (W1) – 0.30 = 4.24%, or $424k on $10m
- 18 (W1) – 0.30 = 4.88%, or $488k on $10m
(W1) The payments in year 2 and year 3 have to be estimated, using the forward interest rates calculated in TYU 1 earlier in this chapter. The 12 – 24 FRA rate for Stone Co was 4.54%, and the 24 – 36 FRA rate was 5.18%.
Hence, to make sure that the fixed payments (X per annum) are equal in present value terms to these expected variable payments:
(X/1.0396) + (X/1.04252) + (X/1.04563) = (366k/1.0396) + (424k/1.04252)
+ (488k/1.04563)
Therefore 0.962X + 0.920X + 0.875X = 352k + 390k + 427k
so 2.757X = 1,169k
X = 1,169k / 2.757
X = $424k
On the $10m debt, this is a rate of 4.24%.
Student Accountant article
The examiner’s article ‘Determining interest rate forwards and their application to swap valuation’ in the Technical Articles section of the ACCA website covers the calculation of swap rates in more detail.
Options over swaps
- Swaptions are hybrid derivative products that integrate the benefits of swaps and options. They are options on swaps.
- The purchaser of an interest rate swaption has the right, but not the obligation, to enter into an interest rate swap at some future date on terms agreed today. An upfront premium is payable.
Swaption illustration
Shun Inc has a $10m loan, repayable in 5 years, at LIBOR + 2%. LIBOR is currently at 5.75%. The company is thus exposed to the risk of fluctuating interest rates.
The treasurer believes that LIBOR will stay low for the next two years, after which period, however, the outlook is at best uncertain. She would like to hedge this risk but is not sure if the current swap rate is the best available. The treasurer wants to lock in the swap rate in two years’ time for the following three years and have the flexibility to benefit from a lower swap rate should swap rates fall.
This is achieved by buying a 2-year option on a 3-year pay fixed 7% swap.
The decision that will have to be made in two years is illustrated below:

Chapter summary
Summary of terminology
| Borrowing | Depositing | |
| FRA | Buy an FRA | Sell an FRA |
| IRG | Call option | Put option |
| Futures | Sell IR futures | Buy IR futures |
| Options | Buy put options | Buy call options |