Hedging foreign exchange risk

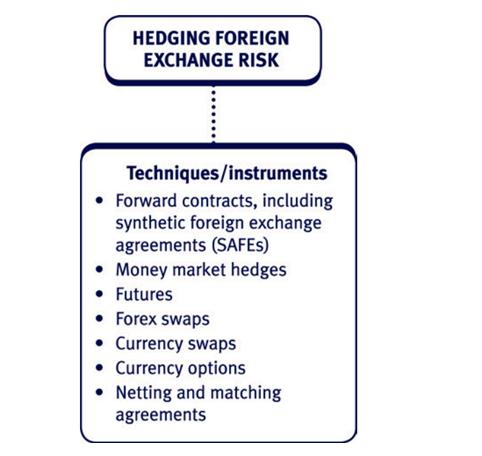
Introduction

 

Types of forex risk

 

Firms may be exposed to three types of foreign exchange risk:

 

Transaction risk

 

• The risk of an exchange rate changing between the transaction date and the subsequent settlement date on an individual transaction.

 

• e. it is the gain or loss arising on conversion.

 

• Associated with exports/imports.

 

• Hedge using a variety of financial products/methods – see below.

 

Economic risk

 

• Includes the longer-term effects of changes in exchange rates on the market value of a company (PV of future cash flows).

 

• Looks at how changes in exchange rates affect competitiveness, directly or indirectly.

 

• Reduce by geographic diversification.

 

Translation risk

 

• How changes in exchange rates affect the translated value of foreign assets and liabilities (e.g. foreign subsidiaries).

 

• Can hedge by borrowing in local currency to fund investment.

 

• Gains/losses usually unrealised so many firms do not hedge.

Types of foreign exchange risk

 

Transaction risk

 

Transaction risk the risk of an exchange rate changing between the transaction date and the subsequent settlement date, i.e. it is the gain or loss arising on conversion.

 

This type of risk is primarily associated with imports and exports. If a company exports goods on credit then it has a figure for debtors in its accounts. The amount it will finally receive depends on the foreign exchange movement from the transaction date to the settlement date.

 

As transaction risk has a potential impact on the cash flows of a company, most companies choose to hedge against such exposure. Measuring and monitoring transaction risk is normally an important component of treasury management.

 

The degree of exposure involved, which is dependent on:

 

• The size of the transaction, is it material?

 

• The hedge period, the time period before the expected cash flows occurs.

 

• The anticipated volatility of the exchange rates during the hedge period.

 

The corporate risk management policy should state what degree of exposure is acceptable. This will probably be dependent on whether the Treasury Department is been established as a cost or profit centre.

 

Economic risk

 

Transaction exposure focuses on relatively short-term cash flows effects; economic exposure encompasses these plus the longer-term effects of changes in exchange rates on the market value of a company. Basically this means a change in the present value of the future after tax cash flows due to changes in exchange rates.

 

There are two ways in which a company is exposed to economic risk.

 

Directly: If your firm’s home currency strengthens then foreign competitors are able to gain sales at your expense because your products have become more expensive (or you have reduced your margins) in the eyes of customers both abroad and at home.

 

Indirectly: Even if your home currency does not move vis-à- vis your customer’s currency you may lose competitive position. For example suppose a South African firm is selling into Hong Kong and its main competitor is a New Zealand firm. If the New Zealand dollar weakens against the Hong Kong dollar the South African firm has lost some competitive position.

Economic risk is difficult to quantify but a favoured strategy is to diversify internationally, in terms of sales, location of production facilities, raw materials and financing. Such diversification is likely to significantly reduce the impact of economic exposure relative to a purely domestic company, and provide much greater flexibility to react to real exchange rate changes.

 

Tutorial note: Borrowing in a foreign currency

 

In addition, when companies borrow in a foreign currency, committing themselves to regular interest payments and principal repayments they are exposing themselves to forex risk. This is a problem that beset a number of Far Eastern companies in the late 1990s. They had borrowed in US dollars or sterling. This became a serious problem when their currency depreciated and the loan repayments became much more expensive. Of course if your firm takes out a loan in dollars and your home currency appreciates against the dollar the loan repayments become cheaper.

 

Translation risk

 

The financial statements of overseas subsidiaries are usually translated into the home currency in order that they can be consolidated into the group’s financial statements. Note that this is purely a paper-based exercise – it is the translation not the conversion of real money from one currency to another.

 

The reported performance of an overseas subsidiary in home-based currency terms can be severely distorted if there has been a significant foreign exchange movement.

 

If initially the exchange rate is given by $1 = £1 and an American subsidiary is worth $500,000, then the UK parent company will anticipate a statement of financial position sheet value of £ 500,000 for the subsidiary. A depreciation of the US dollar to $2 = £1 would result in only £250,000 being translated.

 

Unless managers believe that the company’s share price will fall as a result of showing a translation exposure loss in the company’s accounts, translation exposure will not normally be hedged. The company’s share price, in an efficient market, should only react to exposure that is likely to have an impact on cash flows.

 

However, if the financial manager does want to hedge against the impact of translation risk, trying to make sure that foreign currency assets and liabilities are approximately equal in value is the simplest method. Then any gains or losses in asset values are offset by equivalent losses or gains in the values of the liabilities.

 

This can be achieved by funding foreign asset purchases by borrowing money in the same currency

Hedging transaction risk – The internal techniques

 

Internal techniques to manage/reduce forex exposure should always be considered before external methods on cost grounds. Internal techniques include the following:

 

Invoice in home currency

 

• One easy way is to insist that all foreign customers pay in your home currency and that your company pays for all imports in your home currency.

 

• However the exchange-rate risk has not gone away, it has just been passed onto the customer. Your customer may not be too happy with your strategy and simply look for an alternative supplier.

 

• Achievable if you are in a monopoly position, however in a competitive environment this is an unrealistic approach.

 

Leading and lagging

 

• If an importer (payment) expects that the currency it is due to pay will depreciate, it may attempt to delay payment. This may be achieved by agreement or by exceeding credit terms.

 

• If an exporter (receipt) expects that the currency it is due to receive will depreciate over the next three months it may try to obtain payment immediately. This may be achieved by offering a discount for immediate payment.

 

• The problem lies in guessing which way the exchange rate will move.

 

Matching

 

• When a company has receipts and payments in the same foreign currency due at the same time, it can simply match them against each other.

 

• It is then only necessary to deal on the forex markets for the unmatched portion of the total transactions.

 

• An extension of the matching idea is setting up a foreign currency bank account.

 

• Bilateral and multilateral netting and matching tools are discussed in more detail later in the chapter.

 

Decide to do nothing?

 

• The company would ‘win some, lose some’.

 

• Theory suggests that, in the long run, gains and losses net off to leave a similar result to that if hedged.

 

• In the short run, however, losses may be significant.

 

• One additional advantage of this policy is the savings in transaction costs.

Forward contracts

 

Characteristics

 

A forward contract allows a business to buy or sell a currency on a fixed future date at a predetermined rate, i.e. the forward rate of exchange.

 

 

Test your understanding 1

 

An Australian firm has just bought some machinery from a US supplier for US$250,000 with payment due in 3 months’ time. Exchange rates are quoted as follows:

Spot (US$… to A$1)	0.7785 – 0.7891
Three months forward	0.21 – 0.18 cents premium

 

Required:

 

Calculate the amount payable if a forward contract is used.

 

Availability and use

 

• Although other forms of hedging are available, forward cover represents the most frequently employed method of hedging.

 

• However, the existence and depth of forward markets depends on the level of demand for each particular currency.

 

• In the exam you need to consider; does the forward market exist and would it extend far enough into the future before you recommend it.

 

• For major trading currency like the $, £, Yen or Euro it can be up to

10 years forward. Normally forward markets extend six months into the future. Forward markets do not exist for the so-called exotic currencies.

 

Advantages and disadvantages

 

Advantages		Disadvantages
•	OTC, so can be matched exactly	•	Availability – see above.
	to the future sums involved.	•	Binding contract for delivery,
•	Simple and easy to understand.		even if commercial
			circumstances change – e.g. a
			customer is late paying.
		•	Eliminates exposure to upside as
			well as down-side movements.

Synthetic foreign exchange agreements (SAFEs)

 

• Some governments have banned forward FX trading – usually as a means to reduce exchange rate volatility.

 

• For example:

 

–    Brazilian Reals

 

–    Indian Rupee

 

–    Taiwan Dollars

 

–    South Korean Won

 

–    Chinese Renminbi (or Yuan).

 

• In such markets the use of non-deliverable forwards (NDFs) has developed.

 

• These are like forward contracts, except no currency is delivered. Instead the profit or loss (i.e. the difference between actual and NDF rates) on a notional amount of currency (the face value of the NDF) is settled between the two counter parties.

 

• Combined with an actual currency exchange at the prevailing spot rate, this effectively fixes the future rate in a similar manner to futures.

 

• One other feature is that the settlement is in US dollars.

 

SAFE illustration

 

Let the spot rate between the US$ and the Brazilian Real be 1.6983 Reals to $1 and suppose we agree a 3 month NDF to buy $1 million worth of Reals at 1.7000.

 

If the spot rate moves to 1.6800 in 3 months, then the counter-party will have to pay us 1 million × 0.02 = 20,000 Reals.

 

This will be settled in US$, so the actual receipt will be 20,000/1.6800 = $11,905.

Money market hedges

 

Characteristics

 

• The basic idea is to avoid future exchange rate uncertainty by making the exchange at today’s spot rate instead.

 

• This is achieved by depositing/borrowing the foreign currency until the actual commercial transaction cash flows occur:

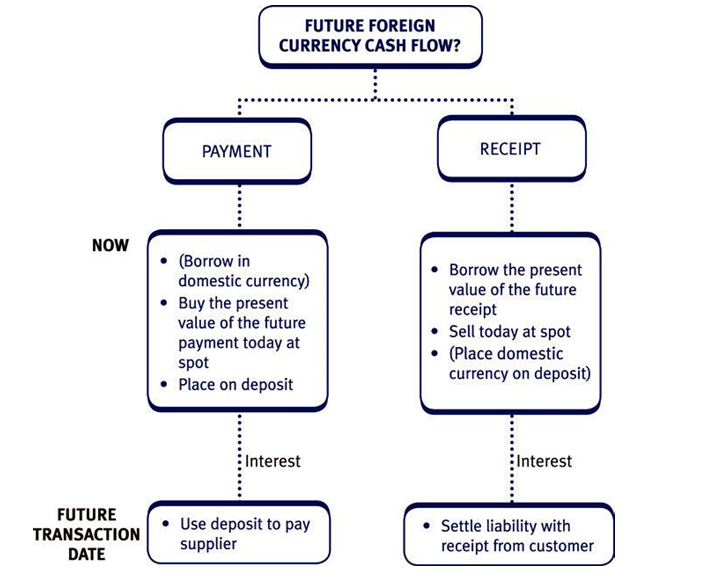
• In effect a foreign currency asset is set up to match against a future liability (and vice versa).

 

 

Test your understanding 2

 

Marcus is based in France has recently imported raw materials from the USA and has been invoiced for US$240,000, payable in three months’ time.

 

In addition, it has also exported finished goods to Japan and Australia.

 

The Japanese customer has been invoiced for US$69,000, payable in three months’ time, and the Australian customer has been invoiced for A$295,000, payable in four months’ time.

Current spot and forward rates are as follows:

 

US$ … /1 Euro
Spot:	0.9830 – 0.9850
3 months forward:	0.9520 – 0.9545
Euro… /1 A$
Spot:	1.8890 – 1.8920
4 months forward:	1.9510 – 1.9540

 

Current money market rates (pa) are as follows:

 

US$:  10.0% – 12.0%

 

A$:     14.0% – 16.0%

 

Euro: 11.5% – 13.0%

 

Required:

 

Show how the company can hedge its exposure to foreign exchange risk using:

 

• forward contracts

 

• money market hedges

 

and for each transaction, determine which is the best hedging technique.

 

Further comments

 

• Interest rate parity implies that a money market hedge should give the same result as a forward contract.

 

• Money market hedges may be feasible as a way of hedging for currencies where forward contracts are not available.

 

• This approach has obvious cash flow implications which may prevent a company from using this method, e.g. if a company has a considerable overdraft it may be impossible for it to borrow funds now.

Arbitrage profits

 

Although the theory of interest rate parity suggests that the financial position should be the same whether a forward contract or a money market hedge is used, in reality there may be differences caused by market imperfections. Then, differences can be exploited by investors aiming to make ‘arbitrage profits’.

 

For example, an investor might be able to earn arbitrage profits by:

 

• borrowing currency X

 

• translating the amount to currency Y and putting the currency Y on deposit

 

• taking out a forward contract to convert Y back into X at some future date

 

• withdrawing the currency Y at the end of the period and translating it back to X under the forward contract

 

• repaying the borrowing in currency X (capital plus any interest accrued), and retaining the surplus.

 

Arbitrage profits will be made here if the forward rate of exchange doesn’t exactly reflect the differential in interest rates between the two countries.

 

4         Futures contracts

 

Characteristics

 

• Futures contracts are standard sized, traded hedging instruments. The aim of a currency futures contract is to fix an exchange rate at some future date.

 

• A key issue with currency futures is to establish the ‘currency of the contract’ or CC. For example if the CC is € and your transaction involves buying €, you should buy futures now to set up the hedge. Note that the CC in an exam question is found by looking at the standard contract size. For example, if the contract size is quoted in $, the CC is $.

Contract sizes – Examples

 

Future		Contract	Price	Tick size	Value of
		size	quotation		one tick
£/US dollar		£62,500	US$ per £1	$0.0001	$6.25
€/US dollar		€200,000	US$ per €1	$0.0001	$20.00
Swiss franc/
US dollar		SFr 125,000	US$ per SFR1	$0.0001	$12.50
Yen/US dollar		12.5 million yen	US$ per 1 yen	$0.000001	$12.50
€/sterling		€100,000	£ per €1	£0.0001	£10
•	The CC is the currency in which the contract size is quoted.

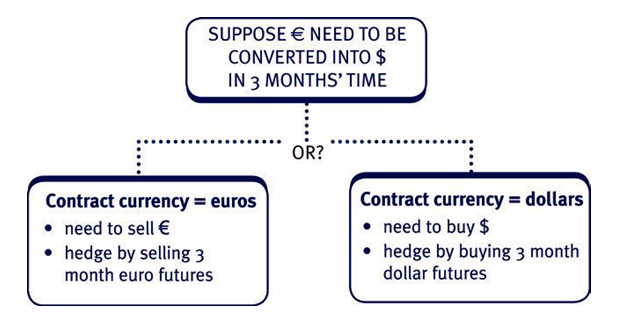
• We assume that the contracts mature or expire at the end of March, June, September and December. It is normal to choose the first contract to expiry after the conversion date.

 

• The range of available futures is limited and includes: $/£, $/Y, $/SFR,

$/A$, $/C$ and $/€. Therefore if you are asked to give a hedge strategy for a ‘minor’ currency you should not recommend a futures contract.

 

Futures hedging calculations

 

Step 1: Set up the hedge by addressing 3 key questions:

 

• Do we initially buy or sell futures?

 

• How many contracts?

 

• Which expiry date should be chosen?

 

Step 2: Contact the exchange. Pay the initial margin. Then wait until the transaction/settlement date.

 

Step 3: Calculate profit or loss in the futures market by closing out the futures contracts, and calculate the value of the transaction using the spot rate on the transaction date.

Futures calculation

 

It is 15 October and a treasurer has identified the need to convert euros into dollars to pay a US supplier $12 million on 20 November. The treasurer has decided to use December Euro futures contracts to hedge with the following details:

 

• Contract size €200,000.

 

• Prices given in US$ per Euro (i.e. €1 = …).

 

• Tick size $0.0001 or $20 per contract.

 

He opens a position on 15 October and closes it on 20 November. Spot and relevant futures prices are as follows:

 

Date		Spot	Futures price
15	October	1.3300	1.3350
20	November	1.3190	1.3240

 

Required:

 

Calculate the financial position using the hedge described.

 

Solution

 

Step 1	(1)	Buy or sell initially?	(1)  CC is €, and we need
	(2)	How many contracts?		to sell € (to buy $), so
				sell futures now.
	(3)	Which expiry date?
			(2)	Cover $12m/1.3350
				(Dec futures price –
				see below) = €8.99
				million, using €200,000
				contracts, hence
				€8.99m/€0.2m = 44.95
				– round to 45
				contracts.
			(3)	Transaction date is
				20 November, so
				choose December
				futures (the first to
				expire after the
				transaction date).
Step 2	Contact the exchange –		Sell 45 December futures
	state the hedge		(at a futures price of
			$1.3350/€1).

	Step 3	Calculate profit/loss in	Initially: Sell at 1.3350.
		futures market by closing	Close out: Buy at 1.3240.
		out the position.
			Difference is $0.011 per €1
			profit.
			45 × €200,000 covered, so
			total profit is 0.011 × 45 ×
			200,000 = $99,000.
		Transaction at spot rate on	Cost in € is €9,022,745.
		20 November:
		Buy $11.901 m extra
		needed at spot rate of
		$1.3190/€1.

 

 

Test your understanding 3

 

It is 4 May and the treasurer of a Swiss company has identified a net receipt of US$2 million on 10 June. These dollars will need to be converted into Swiss Francs (CHF). The treasurer has decided to use US dollar – Swiss Franc futures contracts to hedge with the following details:

 

• New York Board of Trade (NYBOT) options and futures exchange.

 

• Contract size $200,000.

 

• Prices given in Swiss francs per US dollar (i.e. $1 = …).

 

• Tick size CHF 0.0001 or CHF20 per contract.

 

Expiry date	Futures price
June	1.2200
Sept	1.2510

 

The spot rate on 4 May is 1.2160 CHF/$1.

 

Required:

 

Calculate the financial position using the relevant futures hedge, assuming that the spot rate on 10 June is 1.2750 CHF/$1, and that the futures price is 1.2760 CHF/$1.

 

Forecasting futures prices

 

In the examples so far, the closing futures price has been given. This will not be available when the hedge is first set up, so we often try to estimate it to allow us to predict the likely result of the futures hedge.

 

An understanding of ‘basis’ enables us to estimate the closing futures price.

Basis

 

The basis within a futures hedge is defined as:

 

Spot rate – futures price

 

It is easy to calculate the basis when the hedge is first set up, since both the spot rate and the futures price will be known.

 

Also, the basis on the expiry date of the futures contract is always zero.

 

Therefore, the level of ‘unexpired basis’ can be estimated on the transaction date by assuming that the basis reduces from its opening value to zero in a linear manner.

 

 

Why does basis reduce to zero?

 

The futures price at any point in time represents the market’s best estimate of the expected spot rate on the expiry date of the futures contract.

 

i.e. the futures price for a December futures contract is the market’s estimate of the expected spot rate on 31 December.

 

As time goes by and new real world factors come to light, the estimate will change, so the futures price will change.

 

However, as the expiry date approaches, it is likely that the estimate will become more and more accurate until finally, when the expiry date arrives, the estimate will be completely accurate.

 

i.e. the futures price on 31 December, for a December futures contract, will be the same as the spot rate at that date.

 

Therefore, basis will always reduce to zero on the expiry date of a futures contract.

 

 

Illustration 1 – Basis calculation

 

Europe Co is expecting to receive $10m in 4 months’ time, which it wants to translate into €.

 

The spot rate (quoted as €/$1) is 0.7343 – 0.7355.

 

Futures market information: ($500,000 contracts, prices quoted as €/$1)

 

2 month expiry 0.7335

 

5 month expiry 0.7300

 

Required:

 

Estimate the likely financial result of the hedge, assuming that the spot rate in 4 months is expected to be 0.7337 – 0.7366 €/$1, and that basis reduces to zero in a linear manner.

Solution: Hedge details

 

Set up the futures hedge by selling 20 contracts with a 5 month expiry date.

 

Likely result of the hedge:

 

€

 

 

Transaction – sell $10m at spot in 4 months (0.7337€/$1)

 

Futures market: Sell at 0.7300, buy at 0.7328 (from basis workings below)

 

Loss = 0.0028€/$1, multiplied by 20 × $500,000 covered

7,337,000

 

 

 

 

(28,000)

 

––––––––

 

 

Net receipt				7,309,000
				––––––––
Basis workings
	Now	in 4 months		in 5 months
Spot	0.7343	0.7337	(W3)
Futures price	0.7300	0.7328
	––––––	––––––	(W2)	0 (W1)
Basis (difference)	0.0043	0.0009

 

(W1) Basis will reduce to zero by the expiry date of the contract, because on that date, the futures price will equal the (known) spot rate.

 

(W2) Assuming basis reduces in a linear manner, the basis in 4 months should be 1/5 of the original 0.0043 i.e. the unexpired basis is 0.0009.

 

(W3) Basis is the difference between spot and the implied futures price, so implied futures price is 0.7337 – 0.0009 = 0.7328.

 

Exam shortcut – The ‘lock-in rate’

 

The calculation of the likely financial result of the futures hedge was a lengthy calculation, and it also relied upon being able to estimate the spot rate on the transaction date.

 

There is a much simpler way of estimating the likely financial result of the futures hedge, by just calculating the overall ‘lock-in rate’ for the hedge, as follows:

 

Lock in rate = Opening futures price + unexpired basis on the transaction date

 

This will enable you to estimate the likely financial result of the hedge even if the spot rate on the transaction date is not known.

Illustration 2 – The lock-in rate

 

In the Europe Co illustration above, the lock-in rate would be:

 

Opening futures price + unexpired basis on the transaction date = 0.7300 + 0.0009 (from the basis working) = 0.7309€/$1

 

Therefore the likely financial result of the futures hedge is $10m × 0.7309 = €7,309,000, exactly as before.

 

If ever you are asked in the exam to estimate the financial result of a futures hedge, try to use this lock-in rate shortcut if at all possible, because it significantly reduces the amount of workings you’ll need to present in your answer.

 

Basis risk

 

We identified above that basis will fall to zero by the expiry date of the futures contract, but throughout our examples so far we have assumed that the reduction will occur in a linear manner. This might not be the case in reality.

 

Basis risk is the risk that the basis reduces in a non-linear manner, making our forecast of the unexpired basis on our transaction date inaccurate.

 

You will never have to present any more complex calculations in an exam, but make sure you refer to the existence of basis risk in your written answers, to highlight the potential for inaccuracy in your forecast of the unexpired basis and the lock-in rate.

 

5         Currency options

 

Introduction

 

• A currency option is a right, but not an obligation, to buy or sell a currency at an exercise price on a future date. If there is a favourable movement in rates the company will allow the option to lapse, to take advantage of the favourable movement. The right will only be exercised to protect against an adverse movement, i.e. the worst-case scenario.

 

–    A call option gives the holder the right to buy the underlying currency.

 

–    A put option gives the holder the right to sell the underlying currency.

 

• Options are more expensive than the forward contracts and futures.

 

• A European option can only be exercised on the expiry date whilst an American option can be exercised at any time up to the expiry date.

OTC options and exchange traded options

 

Currency options can be bought over the counter (OTC) or from major futures and options exchanges.

 

OTC options

 

• Like forward contracts, the OTC options are tailor made to fit a company’s precise requirements. Branches of foreign banks in major financial centres are generally willing to write options against their home currency.

 

– e.g. Australian banks in Chicago will write options on the Australian dollar.

 

• Option sizes are much larger on the OTC market, with most options being in excess of $1 million.

 

Exchange traded options

 

• Exchange traded options are also available but the OTC market is the larger.

 

– e.g. the London International Financial Futures and Options exchange (LIFFE) offers European style dollar: euro option contracts.

 

 

Traded options example

 

A typical pricing schedule for the US$/€ currency option on the

Philadelphia exchange is as follows.

 

Strike price	CALLS			PUTS
	Jun	Sept	Dec	Jun	Sept	Dec
115.00	1.99	2.25	2.47	0.64	1.32	2.12
116.00	1.39	2.03	2.28	1.00	1.56	–
117.00	0.87	1.55	1.81	1.43	2.22	–
118.00	0.54	1.08	1.30	–	–	–

 

• Here, the options are for a contract size of €125,000 and prices (both strike price and premia) are quoted in US$ (cents) per €1.

 

• So to buy a call option on €125,000 with an expiry date of September and at a strike price of €1 = $1.17 would cost 1.55 cents per euro, or $1,937.50.

 

• Similarly, the premium on a June put at a strike price of 115.00 (€1 = $1.15) would cost 0.64 cents per euro, or $800.

 

• The decision as to which exercise price to choose will depend on cost, risk exposure and expectations. If you have to choose in the exam then one approach is to consider the cost implications only for calculation purposes: The best exercise price is then the one which (incorporating the premium cost) is most financially advantageous.

 

 

Choosing an exercise price

 

Call option

 

Using the above schedule, determine which June call option would give the lowest net cost of acquiring euros.

Strike price	Premium	Total cost per €
115.00	1.99	116.99
116.00	1.39	117.39
117.00	0.87	117.87
118.00	0.54	118.54

 

The lowest cost would involve using call options with a strike price of 115.

 

Put option

 

Using the above schedule, determine which September put option would give the highest net receipt from selling euros.

Strike price	Premium	Net receipt from €1
115.00	1.32	113.68
116.00	1.56	114.44
117.00	2.22	114.78
118.00	–	–

 

The highest receipt would involve using put options with a strike price of 117.

 

Options hedging calculations

 

Step 1: Set up the hedge by addressing 4 key questions:

 

• Do we need call or put options?

 

• How many contracts?

 

• Which expiry date should be chosen?

 

• Which strike price/exercise price should be used?

 

Step 2: Contact the exchange. Pay the upfront premium. Then wait until the transaction/settlement date.

Step 3: On the transaction date, compare the option price with the prevailing spot rate to determine whether the option should be exercised or allowed to lapse.

 

Step 4: Calculate the net cash flows – beware that if the number of contracts needed rounding, there will be some exchange at the prevailing spot rate even if the option is exercised.

 

 

Test your understanding 4 – Pongo

 

Pongo plc is a UK -based import-export company. It has an invoice, which it is due to pay on 30 June, in respect of $350,000.

 

The company wishes to hedge its exposure to risk using traded options.

 

The current $/£ spot rate is 1.5190 – 1.5230.

 

On LIFFE, contract size is £25,000.

 

Exercise price ($/£)                                                      June contracts

 

Calls                               Puts

1.45                                                                                  8.95                                10.20

 

1.50                                                                                  6.80                                12.40

 

Option premia are given in cents per £.

 

Assume that it is now the 31 March.

 

Required:

 

Calculate the cash flows in respect of the payment if the spot rate is: $1.4810 – $1.4850 to £1 on the 30 June.

 

Test your understanding 5 – Pongo (continued)

 

Using the circumstances described in the previous example above, suppose Pongo plc is also due to receive $275,000 from a US customer on 30 September. LIFFE quotes for September option contracts are as follows:

 

Exercise price ($/£1)	September contracts
	Calls	Puts
1.45	14.15	10.45
1.50	8.00	13.40

 

Required:

 

Calculate the cash flows in respect of the receipt if the spot rate is $1.5250 – $1.5285 to £1 on the 30 September.

 

Student Accountant article

 

The article ‘Exchange traded foreign exchange derivatives’ in the Technical Articles section of the ACCA website contains more details on currency futures and options.

Forex swaps

 

Characteristics

 

• In a forex swap, the parties agree to swap equivalent amounts of currency for a period and then re-swap them at the end of the period at an agreed swap rate. The swap rate and amount of currency is agreed between the parties in advance. Thus it is called a ‘fixed rate/fixed rate’ swap.

 

• The main objectives of a forex swap are:

 

– To hedge against forex risk, possibly for a longer period than is possible on the forward market.

 

– Access to capital markets, in which it may be impossible to borrow directly.

 

• Forex swaps are especially useful when dealing with countries that have exchange controls and/or volatile exchange rates.

 

 

Illustration 3

 

Suppose that A plc, a UK construction company, wins a contract to construct a bridge in Argentina. The bridge will require an initial investment now, and will be sold to the Argentinean Government in one year’s time. The Government will pay in pesos.

 

The problem is the company’s exposure to currency risk. They know how much will be received in one year’s time in pesos but not in sterling as the exchange rate changes daily.

 

Various possible hedging strategies:

 

• Decide to do nothing, i.e. accept the risk – win some, lose some.

 

• Lock into a forward contract for converting the amount receivable in one year’s time into sterling, if a forward market exists.

 

• Undertake a money market hedge: take out a loan in pesos to cover the initial cost, and repay the loan from the disposal proceeds in a year’s time. We would then only be exposed on the profit we make (if we make any).

 

• Enter into a forex swap. Instead of taking out a loan in pesos we

 

• Swap sterling today for the pesos required to cover the initial investment, at an agreed swap rate.

 

• Take out a loan in sterling today to buy the pesos.

 

• In one year’s time (in this example) arrange to swap back the pesos obtained in (a) for pounds at the same swap rate.

 

Just like taking out a loan in pesos we are therefore only exposed on the profit that we make. We could of course use another hedging technique to hedge the profit element.

Calculations

 

Illustration 4

 

Say the bridge will require an initial investment of 100m pesos and is will be sold for 200m pesos in one year’s time.

 

The currency spot rate is 20 pesos/£, and the government has offered a forex swap at 20 pesos/£. A plc cannot borrow pesos directly and there is no forward market available.

 

The estimated spot rate in one year is 40 pesos/£. The current UK borrowing rate is 10%.

 

Required:

 

Determine whether A plc should do nothing or hedge its exposure using the forex swap.

 

Solution
£m	0	1
Without swap
Buy 100m pesos @ 20	(5.0)
Sell 200m pesos @ 40		5.0
Interest on sterling loan (5 × 10%)		(0.5)
	––––	––––
	(5.0)	4.5
	––––	––––
With forex swap
Buy 100m pesos @ 20	(5.0)
Swap 100m pesos back @ 20		5.0
Sell 100m pesos @ 40		2.5
Interest on Sterling loan (5 × 10%)		(0.5)
	––––	––––
Net receipt of (£2.0 million)	(5.0)	7.0
	––––	––––

 

A plc should use a forex swap.

 

(Key idea: The forex swap is used to hedge foreign exchange risk. We can see that in this basic exercise that the swap amount of 100m pesos is protected from any deprecation, as it is swapped at both the start and end of the year at the swap rate of 20, whilst in the spot market pesos have depreciated from a rate of 20 to 40 pesos per pound.)

Test your understanding 6

 

Goldsmith Co, a mining company based in the fictitious country of Krownland, wishes to hedge 1 year foreign exchange risk, which will arise on an investment in Chile. The investment is for 800m escudos and is expected to yield an amount of 1,000m escudos in 1 year’s time.

 

Goldsmith cannot borrow escudos directly and is therefore considering two possible hedging techniques:

 

• Entering into a forward contract for the full 1000m escudos receivable.

 

• Entering into a forex swap for the 800m escudos initial investment, and then a forward contract for the 200m escudos profit element.

 

The currency spot rate is 28 escudos to the krown, and the bank has offered a forex swap at 22 escudos/krown with Goldsmith making a net interest payment to the bank of 1% in krowns (assume at T1).

 

Interest rates	Borrowing	Lending
Krownland	15%	12%
Chile	N/A	25%

 

A forward contract is available at a rate of 30 escudos per krown.

 

Required:

 

Determine whether Goldsmith should hedge its exposure using a forward contract or a forex swap.

 

7         Currency swaps

 

Characteristics

 

• A currency swap allows the two counterparties to swap interest rate commitments on borrowings in different currencies.

 

• In effect a currency swap has two elements:

 

– An exchange of principals in different currencies, which are swapped back at the original spot rate – just like a forex swap.

 

– An exchange of interest rates – the timing of these depends on the individual contract.

 

• The swap of interest rates could be ‘fixed for fixed’ or ‘fixed for variable’.

Example of a currency swap

 

Warne Co is an Australian firm looking to expand in Germany and is thus looking to raise €24 million. It can borrow at the following fixed rates:

 

A$ 7.0%

 

€ 5.6%

 

Euroports Inc is a French company looking to acquire an Australian firm and is looking to borrow A$40 million. It can borrow at the following rates:

 

A$ 7.2%

 

€ 5.5%

 

The current spot rate is A$1 = €0.6.

 

Required:

 

Show how a ‘fixed for fixed’ currency swap would work in the circumstances described, assuming the swap is only for one year and that interest is paid at the end of the year concerned.

 

Solution

 

Timing                                                                 Warne Co                                                                                 Euroports Inc

 

Now                               Borrow from              A$40m at 7.0%    €24m at 5.5%

banks

 

 

Exchange                   Pay A$40m to

principals                    Euroports

receive €24m

 

End of year               Pay interest to         Pay A$2.8m

banks                           interest

 

Exchange                   Pay €1.32m to

interest                        Euroports

receive A$2.8m

 

Swap back                Pay €24m to

principals                    Warne receive

A$40m

 

Net result:

Pay €24m to

Warne receive

A$40m

 

Pay €1.32m

interest

 

Receive €1.32m Pay A$2.8m to Warne

 

Pay A$40m to

Euroports

receive €24m

 

 

Interest costs	Warne Co	Euroports Inc
Without swap (24 × 5.6%)
(40 × 7.2%)	€1.344m	A$2.88m
With swap	€1.320m	A$2.80m
	––––––––	––––––––
Saving	€24,000	A$80,000
	––––––––	––––––––

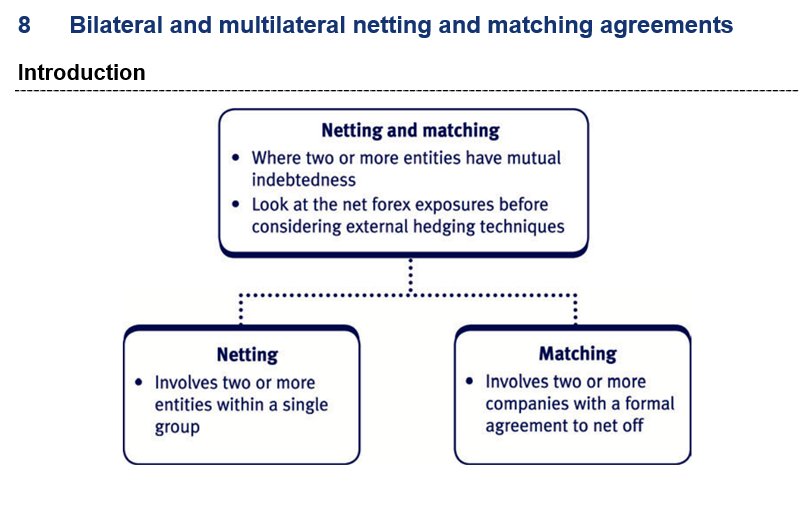
Netting and matching

 

Netting and matching are carried out to reduce the scale of external hedging required.

 

For example, Group X is expecting to receive $10 million in one subsidiary and pay $6 million at the same time in another subsidiary. Clearly the group only has a net exposure of a receipt of $4 million.

 

The terms ‘netting’ and ‘matching’ are often used interchangeably but strictly speaking they are different:

 

• Netting refers to netting off group receipts and payments, as in the example above.

 

• Matching extends this concept to include third parties such as external suppliers and customers.

 

When is multilateral netting used?

 

Multilateral netting involves minimising the number of transactions taking place through each country’s banks. This limits the fees that these banks receive for undertaking the transactions and therefore some governments do not allow multilateral netting in order to maximise the fees their local banks receive.

 

On the other hand, some other governments allow multilateral netting in the belief that this will make companies more willing to operate from those countries and any banking fees lost will be more than compensated by the extra business these companies and their subsidiaries bring into the country.

 

Calculations

 

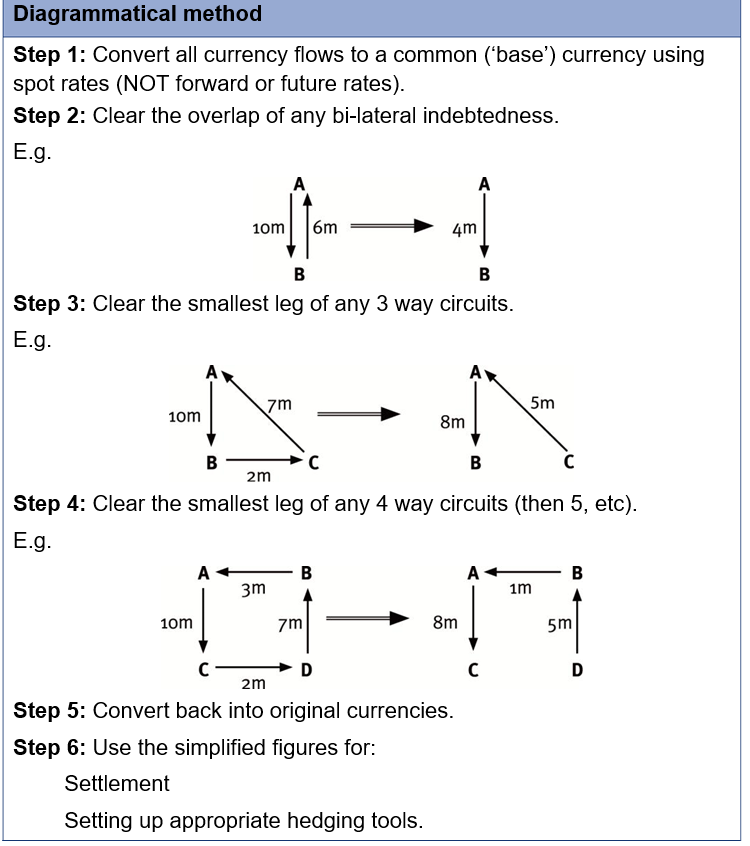
The calculations can be presented in one of two ways: the tabular method and the diagrammatical method.

 

Tabular method (‘transactions matrix’)

 

Step 1: Set up a table with the name of each company down the side and across the top.

 

Step 2: Input all the amounts owing from one company to another into the table and convert them into a common (base) currency (at spot rate).

 

Step 3: By adding across and down the table, identify the total amount payable and the total amount receivable by each company.

 

Step 4: Compute the net payable or receivable, and convert back into the original currency.

Multilateral netting – Worked example

 

P is the parent company of a group that contains 3 subsidiaries: Q (based in Europe), R (based in the USA) and S based in Canada. The following cash flows are due in 2 months’ time between P and its subsidiaries:

 

Owed by	Owed to	Amount
P	S	CAN$ 3 million
P	R	US$ 5 million
Q	R	US$ 4 million
Q	S	CAN$ 7 million
R	S	CAN$ 2 million
R	P	US$ 6 million
S	Q	EUR 12 million
S	P	CAN$ 5 million

 

Mid-rate exchange rates in two months’ time are expected to be:

 

£1 = US$ 1.60

 

£1 = EUR 1.20

 

£1 = CAN$ 1.50

 

Required:

 

Calculate, using a tabular format (transactions matrix), the impact of undertaking multilateral netting by P and its three subsidiary companies for the cash flows due in two months.

 

Solution

 

Note that all foreign currency amounts have been translated into £ using the given mid rates.

 

In £ million			Paid	by
Paid to	P	Q	R	S	Total
P			3.750	3.333	7.083
Q				10.000	10.000
R	3.125	2.500			5.625
S	2.000	4.667	1.333		8.000
Total payment	(5.125)	(7.167)	(5.083)	(13.333)
Total receipt	7.083	10.000	5.625	8.000
Net receipt/(payment)	1.958	2.833	0.542	(5.333)

 

So overall, S needs to pay amounts equivalent to the above figures to each of P, Q and R in two months’ time.

Test your understanding 8 – Netting and matching

 

X, Y, and Z are three companies within the same UK based international group. W is a company outside of the group. The following liabilities have been identified for the forthcoming year:

 

Owed by	Owed to		Amount (millions)
X	Y		€39
Y	X		£10
Y	W		$20
Z	X		¥200
Z	Y		€15
W	X		$15
W	Z		¥100
Mid-market spot rates are:		£1	= $2.00
		£1	= €1.50
		£1	= ¥250

 

Required:

 

Establish the net indebtedness that would require external hedging.