FRIDAY: 21 May 2021. Time Allowed: 3 hours.
Answer ALL questions. Marks allocated to each question are shown at the end of the question. Show ALL your workings.
QUESTION ONE
1. Differentiate between “correlation analysis” and “regression analysis”. (2 marks)
2. Compu World Limited assembles and sells computers. The company estimates that if it optimally assembles computers, it could sell between 1,100 and 2,000 computers per month and the monthly revenue (in thousands of shillings) over this range of sales could be represented by the function 
The fixed cost of the company amounts to Sh.100,000 per month. If is assumed that all the computers assembled in a given month are sold within the same month.
Required:
The total cost function. (2 marks)
The profit function,. (2 marks)
The optimal monthly output. (3 marks)
The maximum profit of the company. (2 marks)
3. The Registrar of Highfliers University has observed that the grade point aggregate of the University’s students is normally distributed with a mean of 2.75 and a standard deviation of 0.40.
Required:
The probability that a randomly selected student from the university has a grade point aggregate of between 2.00 and 3.00. (3 marks)
The lowest grade point aggregate that should be obtained by a student for him/her to be among the top ten per cent of the students. (3 marks)
Assuming that the university has a total of 10,000 students, determine the number of students having. a grade point aggregate of 3.70 or higher. (3 marks)
(Total: 20 marks)
QUESTION TWO
1. Highlight two properties of each of the following probability distributions:
Binomial distribution. (2 marks)
Poisson distribution. (2 marks)
2. Enumerate two advantages and two disadvantages of the ordinary least squares method of forecasting. (4 marks)
3. An investor intends to purchase shares in one of three companies, A, B and C. The three companies have varying
degrees of sensitivity to the state of the economy. There are three states of the economy classified as weak, moderate or strong. The investor has constructed the following pay off table for the profits under the three states of the economy, in millions of shillings.
State of the economy
Company Weak Moderate Strong
A -4.0 3.5 6.0
B -2.0 2.5 4.5
C -2.4 2.8 3.5
The probabilities for the three states of the economy are 0.2, 0.4 and 0.4 for weak, moderate and strong respectively.
Required:
Advise the investor on the best course of action based on the:
Maxmin criterion. (2 marks)
Maxmax criterion. (2 marks)
Minimax regret criterion. (3 marks)
Expected value of perfect information. (5 marks)
(Total: 20 marks)
QUESTION THREE
1. A baker makes and sells cakes to students through their cafeteria system. The distribution of cakes produced and cakes sold for the last 250 weeks is as follows:
Number of weeks
Cakes Cakes
Number of cakes Produced Sold
150 20 35
250 50 50
350 80 80
450 80 65
500 20 20
Each cake costs Sh.80 to make and is sold for Sh.120 if sold during the week of production, otherwise it is sold during the second week at Sh.60. If not sold during the second week, the cake’s value drops to zero and the baker suffers the total loss of production. Weekly demand is satisfied from the week’s production and any demand remaining unsatisfied is satisfied from the stock of the previous week. A stock out costs the baker Sh.20 per cake.
The following random numbers are applicable:
Cakes produced 33, 86, 50, 41, 31, 78, 30, 22, 26, 88
Cakes sold 79, 03, 40, 13, 58, 61, 72, 49, 82, 86
Required:
Simulate the baker’s average weekly profit over an 8-week period. (10 marks)
2. Kazi na Bidii Ltd. sells four types of products. The resources needed to produce one unit of each product and the sales prices are given as follows:
Cost and resources requirements for Kazi na Bidii Ltd.
Resource Product 1 Product 2 Product 3 Product 4
Raw materials (units) 2 3 4 7
Labour hours 3 4 5 6
Sales price (Sh.) 4 6 7 8
Additional information:
- Currently, 4,600 unfits of raw materials and 5,000 labour hours are available.
- To meet customers’ demand, exactly 950 total units must be produced and at least 400 units of Product 4 must be produced.
- A computer output of the above linear programming model has been given as follows:

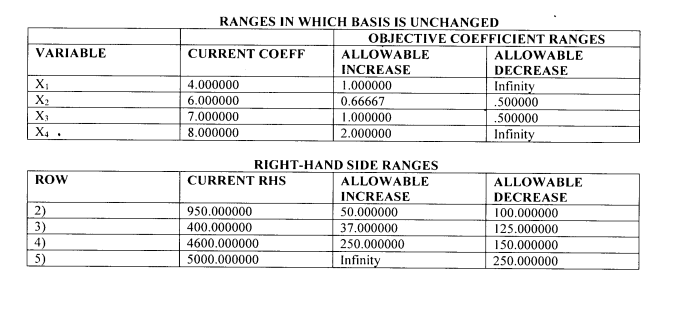
Required:
The optimal solution to the problem. (2 marks)
The optimal solution if the company raises the price of product 2 by Sh.0.50 per unit. (2 marks)
The optimal Z-value if a total of 980 units must be produced. (3 marks)
The optimal Z-values where 4,500 units and 4,400 units of raw materials are available. (3 marks)
(Total: 20 marks)
QUESTION FOUR
1. Enumerate eight applications of quantitative analysis in business. (8 marks)
2. The following is a pay-off matrix of a zero sum two person game:

Required:
The optimal plan for both players. (5 marks)
3. A beauty therapist has observed that the mean arrival rate in her beauty parlour is 6 customers per hour and the mean service rate is 8 customers per hour. The beauty parlour operates a 12 hour day.
A more efficient machine for use by the therapist is available for purchase. If the machine is purchased by the therapist, it would increase the average service rate at the parlour to 12 customers per hour. The cost of each hour lost due to a customer waiting for service is Sh.875.
Required:
The average waiting cost per day. (3 marks)
Evaluate the effect of purchasing the more efficient machine on the average daily waiting cost. (4 marks)
(Total: 20 marks)
QUESTION FIVE
1. Citing an example in each case, explain the difference between a continuous function and a discrete function. (4 marks)
2. X Ltd. is considering undertaking a project which fequires the following resources:
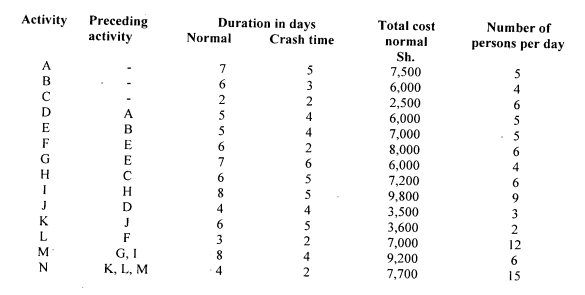
The cost of crashing an activity per day is,Sh.1,000.
Required:
Using network analysis, determine:
The project’s normal duration, normal cost and critical path. (8 marks)
The minimum time in which the project could be completed and the cost of the project. (8 marks)
(Total: 20 marks)
