WEDNESDAY: 6 December 2023. Morning Paper. Time Allowed: 3 hours.
This paper has seven (7) questions. Answer any FIVE questions. ALL questions carry equal marks. Show ALL your workings. Do NOT write anything on this paper.
QUESTION ONE
1. Highlight FOUR disadvantages of the mode as a measure of central tendency. (4 marks)
2. Find the area between the curve y = x + 2x + 1 , the x axis and the lines x = 1 and x = 2. (4 marks) x2
3. Safi Limited manufactures and sells two types of cleaning pads; Osha and Oga. The demand functions for the two products are given by:

The total cost of producing both products is given by the function TC = 230x + 90y.
Required:
The number of units of each product required to maximise total profit. (10 marks)
The maximum total profit. (2 marks)
(Total: 20 marks)
QUESTION TWO
1. List SEVEN steps of the decision making process. (7 marks)
2. The following data shows the quarterly sales of cars for Excellent Auto Enterprises for a period of three years:

Required:
The 4-quarter centred moving average trend values. (4 marks)
The seasonal multiplicative indices. (5 marks)
The deseasonalised sales for each quarter. (4 marks)
(Total: 20 marks)
QUESTION THREE
1. Highlight FOUR applications of Markov chain analysis in business and finance. (4 marks)
2. An insurance company has 2 claim assessors who must each give approval to customers who wish to lodge a claim for compensation. The manager currently has 8 such customers and has asked each assessor to independently rank the customer claims in order of merit. The rankings are shown below:
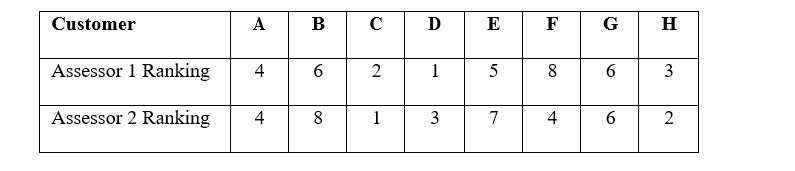
Required:
Calculate the rank correlation coefficient of the two sets of rankings and comment on the results. (8 marks)
3. The Revenue Authority Research Department conducted a survey that revealed the number of companies that were reported as being tax compliant in the last six months of the year 2022 as recorded in the table below:

Required:
Test the hypothesis that the number of tax compliant companies does not depend on the month of the year at a 1% significance level. (8 marks)
(Total: 20 marks)
QUESTION FOUR
1. An economy is based on 2 sectors; Agriculture and Manufacturing. Production of a shilling worth of Agriculture requires an input of 0.3 from the Agriculture sector and 0.1 from the Manufacturing sector.
Production of a shilling worth of manufacturing requires an input of 0.2 from the Agriculture sector and 0.4 from the Manufacturing sector.
Required:
Find the output from each sector that is needed to satisfy a final demand of Sh.12 billion for Agriculture and Sh.8 billion for Manufacturing. (8 marks)
2. Consider the following data for 120 students of a College concerning the languages they are studying namely;
French, German and Russian.
- 15 students study Russian and German.
- 58 students study German or French but not Russian.
- 28 students study French only.
- 90 students study French or German.
- 20 students study French and Russian.
- 44 students study at least two of the three languages.
- 20 students do not study any of the three languages.
Required:
Present the above information in a Venn diagram. (6 marks)
Number of students who study all the three languages. (2 marks)
Proportion of students who study French. (2 marks)
Number of students who study at least one language. (2 marks)
(Total: 20 marks)
QUESTION FIVE
1. Explain the terms “minimax criterion” and “maximax criterion” as used in decision analysis. (4 marks)
2. Viwanda Ltd. produces light bulbs that are packed into boxes of 100. The company’s quality control department indicates that 0.5% of the light bulbs produced are defective.
Required:
The percentage of boxes that will contain no defective light bulbs. (1 mark)
The percentage of boxes that will contain two or more defective light bulbs. (3 marks)
3. An accountant wishes to undertake a cost analysis of the annual repair cost for a popular model of a machine as influenced by the age of the machine. The results obtained are shown below:

Required:
Pearson’s coefficient of correlation between the age of the machine and the repair cost. Interpret your
result. (4 marks)
Fit a least squares regression line of repair cost on age of machine to the data. (4 marks)
Interpret the meaning of regression coefficients a and b in the least squares regression line obtained in 3 (ii) above. (2 marks)
The coefficient of determination. Interpret your result. (2 marks)
(Total: 20 marks)
QUESTION SIX
1. Explain FOUR limitations of quantitative analysis. (4 marks)
2. The amount of money spent on purchases by the first 50 customers at a large department store is summarised in the following table:

Required:
Compute:
The mean amount spent by the 50 customers. (4 marks)
The standard deviation of the amount spent by the 50 customers. (4 marks)
The coefficient of variation of the amount spent by the 50 customers. (2 marks)
The coefficient of Kurtosis and comment on your answer. (6 marks)
(Total: 20 marks)
QUESTION SEVEN
1. Explain the following terms as used in statistics:
Sample statistic. (2 marks)
Population parameter. (2 marks)
Sampling distribution. (2 marks)
2. A manufacturer of dresses makes two types of dresses; Standard and Executive. Each Standard dress requires 10 labour hours from the cutting department and 30 labour hours from the sewing department. Each Executive dress requires 20 labour hours from the cutting department and 40 labour hours from the sewing department. The maximum labour hours available in the cutting department and the sewing department are 320 and 540 respectively. The company makes a profit of Sh.500 on each Standard dress and Sh.800 on each Executive dress.
Required:
Formulate a mathematical model for the above linear programming problem. (4 marks)
Using the simplex method, determine the number of Standard and Executive dresses that should be
produced in order to maximise profit. (10 marks)
(Total: 20 marks)
