This is the level of output at which total profit is at maximum. It is the best or the most efficient size of a firm when the long run average cost of a firm is at minimum. At this point there will be no motive for further expansion since at any other size large or smaller
the firm will be less efficient. This is also attained when the firm cost of production is at its minimum level as illustrated in Figure 4.9
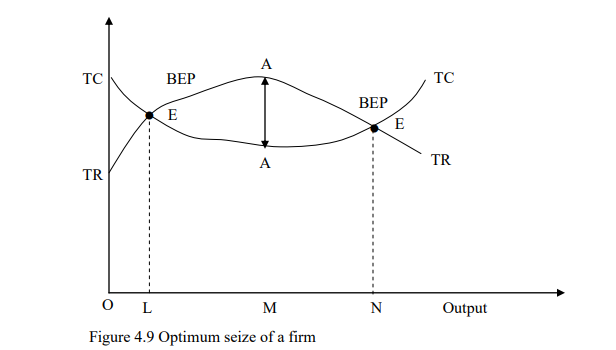
Below OL total cost exceeds total revenue and hence the firm is making loss. At the point EL neither profit nor loss are being made and hence its break even point (BEP) when total revenue is equal to the total cost. The same case applies to the point EN.
Maximum profit lies where revenue and total cost difference total in the greater i.e. the point where the vertical distance between the total revenue and the total cost is greatest. In Figure 4.9 the maximum profit is at point M where AA is the largest vertical distance.
N/B: For profit maximization the following two conditions must be met
- The necessary conduction – according to this conduction profit are maximized at the levels of output where marginal revenues is equal to marginal cost. To maximize profits profit is symbolized by pie ( ∏ )

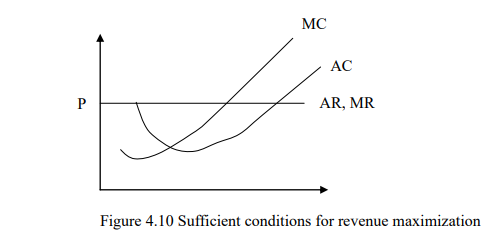
- The sufficient condition states that the slope of marginal revenue curve must be less than the slope of marginal cost curve at the point where they meet. Meaning that the marginal cost curve cuts the marginal revenue curve from below as shown in Figure 4.10
N/B: Total profit function is maximized as follows
- Taking the first derivative and setting it equal to zero to obtain the critical values.
- Taking the second derivative and evaluating it at the critical values to ascertain if the function is at the relative minimum or maximum.
