INTRODUCTION
Network analysis looks at the way large projects such as construction projects, computerisation projects or managerial projects are planned and executed. The objective of network analysis is to set out a framework or plan such that the project is carried out and completed efficiently.
DRAWING A NETWORK DIAGRAM
Supposing a project is to build a house. Then in network analysis each stage of the process would be itemized and the time taken to do each part estimated. The logical sequence of events would also be thought through and written down. A network or diagram of the events would then be drawn up and the critical path identified.
The critical path
If all the various ways (paths) through a network are identified and timed, the path with the longest time is known as the critical path. If an activity on the critical path is delayed, then the entire project will be delayed. Activities on the critical path must finish on time if the project is to finish on time.
A network diagram essentially illustrates graphically the most efficient way of carrying out a particular project.
Once the basic concepts of drawing the network have been understood you can then complete the analysis of the network. This involves adding the duration or time that each activity takes and establishing the critical path through the network. It is often also necessary to find the earliest and latest event times.
Usually in exams you are given what is called a precedence table. The following table is an example of a typical precedence table. The activities could relate to any project. In this case let us assume it relates to building a garage.
Table 15.1
| Activity
|
Preceding activity
|
Time for
(duration)
|
each
|
activity
|
| A. Buy bricks
|
– (None)
|
2
|
|
|
| B. clear site
|
–
|
3
|
|
|
| C. sort bricks
|
A
|
4
|
|
|
| D. lay bricks
|
B
|
1
|
|
|
| E. put on roof
|
CD
|
7
|
|
|
Usually in an exam you are asked to
− Draw the network based on the table.
− Find the critical path. This is the longest path through the network.
The Rules
There are various rules associated with drawing a network. These are as follows:
Rule 1
Each network starts and ends at just one point or node. The starting points are called nodes and the arrows joining the nodes are called activities. The diagram below represents a very simple network which would be written as follows.
Table 15.2
| Activity
|
Preceding activity
|
Duration
|
| A
|
– | 2 weeks
|
| B
|
A
|
3 weeks
|
| C
|
B
|
2 weeks
|
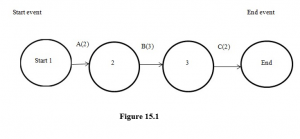
A starts at the beginning, B comes after A and C comes after B. The figures in brackets represents the duration of each activity. The time to finish this project would be 7 weeks. (2+3+2). This network is the simplest type.
Rule 2
When drawing networks, the activities, arrows, cannot cross over each other.
Rule 3
The final rule is that two activities cannot start and end at the same node.
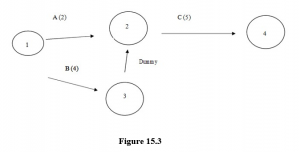
What is a dummy variable and when do you use one?
If the details of the network lead to two activities starting and finishing at the same nodes, it is avoided using a Dummy variable. This is an activity that just links nodes together. No duration attaches to it. For example:
Table 15.3
| Activity | Preceding activity | Duration of activity |
| A | – | 2 |
| B | – | 4 |
| C | AB | 5 |
In the above example, activities A & B both start at the beginning and must finish together before C can start. The network for this should be drawn as follows: the nodes are numbers for clarity so in the example below it would not matter if the 1 and 2 nodes were reversed. What is important with network analysis is that the network is logical and adheres to the rules of network drawing. Remember to always start and finish at one point only and the network should progress from left to right.
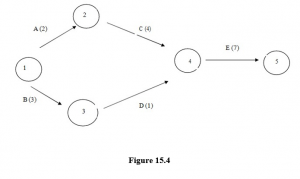
EXAMPLES
We are now ready to do the example at the start of this section:
Table 15.4
| Activity
|
Preceding activity
|
Time for each
(duration)
|
activity
|
| A
|
– (None)
|
2
|
|
| B
|
–
|
3
|
|
| C
|
A
|
4
|
|
| D
|
B
|
1
|
|
| E
|
CD
|
7
|
|
− Draw the network based on the table.
− Find the critical path. This is the longest path through the network. A+C+E = 2+4+7=13