3.1 Money demand
The demand for money is the desired holding of financial assets in the form of money, that is, cash or bank deposit. It can refer to the demand for money narrowly defined as M1 (non-interest bearing holding) or for money in the broader sense of M2 or M3.
3.1.2 The classical view of money demand
The classical view of money demand considers income to be primary determinant of money demand. The higher your income, the greater the amount of money you will hold.
The simple quantity theory
Irving Fisher developed the simple quantity theory of money demanded which views transactions as the primary motive for holding money. It has roots in the equation of exchange that links aggregate pending in an economy and the stock of money. To illustrate the development of fisher’s idea about money demand, we consider a simple economy in which total spending in a year (TS) is $1,000 and the stock of money (M) is $ 200.
Why can individuals in the economy buy $1,000 worth of goods and services if the money stock is only $200?
The answer is that on average each dollar is used more than once in a year. In fact, in this example each dollar must be used on average of five times in a year for a money supply of $ 200 to support $ 1,000 of spending.
The number of times an average unit of money changes hands in a year is called velocity (V).
We can write the equation of exchange as M x V =TS
This equation state that money supply in the economy (M) multiplied by the number of times the average unit of money changes hands in one year (V) will equal the value of annual total spending (TS).
The equation of exchange provides a useful way to think about money and the economy. The equation of exchange is not a theory bur an identity. To determine the velocity we simply divide total spending by the money supply and obtain:
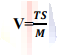
This equation of exchange is important because it tells us that if the quantity of money increases, either total spending will increases, velocity fall, or both. In our example, total spending is $1,000, velocity is 5, and the quantity of money is $ 200. If the quantity of money increases to $ 400 and velocity stays constant, total spending must increase to $ 2000. This is because the economy now has $ 400 of money, and if everyone spends this money at a rate that causes it to change hands five times in a year, spending will have to be:
$ 400 X 5 = $ 2000
If the money supply increases to $ 400 but total spending stays at $ 1,000. Then we know velocity has fallen to 2.5. With $ 400 of money and spending at $ 1000, money must change hands 2.5 times in one year, on average.
To develop a theory of money demand, Fisher reasoned that velocity would be constant since it depends on slowly moving variables such as the frequency with which people are paid and institutional characteristics of payment system. This line of reasoning implies the equation of exchange can be used to write money demand as:
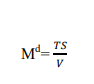
Since velocity was thought to be constant, any increase in total spending would lead to an increase in the demand for money. The idea was that with constant velocity, an increase in spending requires greater money holding, to satisfy the equation of exchange. Thus, money demand was linked to the desire to make transactions. This is why we say the simple quantity theory is based on the transactions motive for holding money.
Fisher had further insight into money demand, which he got from considering how total spending could change. Fisher separated total spending (TS) into the quantity of goods purchased (Y) and the price of those goods (P):
TS=P x Y
Using this formula, we can write the equation of exchange as
M x V= P x Y
Then the simple quantity theory of money demand becomes
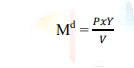
This version of the quantity theory of money demand stresses that people will want to hold money if either the prices of goods they want to purchase increase or the quantities they want to purchase increase. In either case, the amount of money required to pay for the purchase of these goods will increase.
Suppose people are purchasing 1,000 goods at a price of $1 each. From our previous example velocity is 5, so money demand is $ 200, calculated as
What happens if the prices of the goods double to $ 2 each? If people still want to purchase $1,000 goods they will now make purchases in the amount of $ 2,000 per year. With velocity constant of 5, this increases money demand to
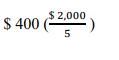
Alternatively, consider what happens if the number of goods people want to purchase rises to $ 2,000, but the price of each stays at $ 1. In this case, the dollar amount of purchase is also $ 2000, so with velocity at 5, money demand is again $ 400. Thus with velocity constant, increase in the price level have the same effect on money demand as do increase in the number of goods and services purchased.
As long as the physical amount of purchase stays constant, any increase in prices will be matched by a proportional change in money demand. Thus, the simple quantity theory of money demand is often called a theory of the demand for real money balances. Real money balances are the nominal money stock divided by the price level (M/P) and are a measure of the purchasing power of money.
For a give quantity of dollars, M, increase in the price level mean less can be purchased. Increase in purchasing power come about from either an increase in the money stock (M), or a reduction in the price level (P), while decrease in purchasing power result from either a decrease in the money stock or an increase in the price level.

Since the simple quantity theory of money views velocity in equation above as constant, the demand for real money balances depends solely on real income. If real income doubles, real money balances double as well, i.e. twice as many real balances would be needed to make transactions.
3.1.2 Keynes’s view of money demand
The modern view of money demand owes much to the work of John Maynard Keynes in the 1930s. While classical economists tended to emphasize the use of money in making transactions, Keynes identified three motives for holding money.
1. Transaction motive
People hold money because it is useful in making purchases. Naturally the transaction motive for holding money would give rise to money demand that is positively related to income. People with higher incomes typically make transactions and thus will hold more money. In fact, like the classical economists, Keynes viewed money held for transaction purposes as being proportional to income.
2. Precautionary motive.
People hold money to meet unexpected expenditure requirements, such as for emergencies or the proverbial rainy day. This is a refinement of the store of wealth function of money. Keynes also viewed money held for precautionary purposes as being proportional to income.
3. Speculative motive
The most novel/new idea in Keynes‟s theory of money demand was the speculative motive, which implies money demand depends on interest rates. In this respect people may choose to keep ready money to take advantage of profitable opportunities that may arise in financial markets such as to invest in bonds which may arise or they may sell bonds for money when they fear a fall in bonds market prices.
3.2 Money supply
The money supply/money stock is the total amount of money available in an economy at a particular point in time. There are several ways to define “money”, but standard measures usually include currency in circulation and demand deposits ( depositors easily accessed assets on the books of financial institutions).
Money supply data are recorded and published, usually by the government or the central bank of the country. Public and private sector analysis have long monitored changes in money supply because of its possible effects on the price level, inflation and business cycle.
In a simplified definition of quantity of money, money supply is the number of dollars/shillings held by the public, and we assumed that the federal reserve/central bank controls the supply of money by increasing or decreasing the number of dollars in circulation through Open-Market Operations (OMO).
Although this explanation is a good first approximation, it is incomplete, for it omits the role of the banking system in determining the money supply. Money supply is determined not only by central bank‟s policy, but also by the behavior of households which hold money and of banks in which money is held.
Money supply includes both currency in the hands of the public and deposits at banks that household can use on demand (i.e. when they need the money) for transactions, such as checking account. If M=money supply, C=currency in the handsof the public, and D=demand deposit, then we can write
Money supply= currency in the hands + demand deposit
M= C+ D
To understand the money supply, we must understand the interaction between currency in the hands and how policy influences these two components of the money supply.
100-percent reserve banking
Suppose that banks accept deposits but do not make loans. The only purpose of the bank is to provide a safe place for depositors to keep their money. The deposits that banks have received but have not lent out are called reserves. Some reserves are held in the volt of local banks through the country, but most are held at central bank, such as the Federal Reserve.
In our hypothetical economy, all deposits are held as reserves, that is, banks simply accept deposit, place the money in reserve, and leave the money there until the depositor makes a withdrawal or writes a check against the balance. This system is called 100-percent-reserve banking.
Unlike banks in our economy, this bank is not making loans, so it will not earn profit from its assets. The bank presumably charges depositors a small fee to cover its costs. A dollar deposited in a bank reduces currency in the by 1 dollar and raises deposit by 1 dollar, so the money supply remains the same. If banks hold 100 percent of deposit in reserve, the banking system does not affect the supply of money.
3.2.2 Fractional-reserve banking
Now imagine that banks start to use some of the deposit to make loans, for example to families who are buying houses or to firms that are investing in new plants and equipment. The advantage to the banks is that they can charge interest on the loans. The banks must keep some reserves on the hand so that reserves are available whenever depositors want to make withdrawals. But as long as the amount of new deposits approximately equals the amount of withdrawals, a bank need not keep all its deposits in reserve. Thus, bankers have an incentive to make loans. When they do so, we have fractional-reserve banking, a system under which banks keep only a fraction of their deposit in reserve.

This balance sheet assumes that the reserve-deposit ratio (the fraction of deposits kept in reserve) is 20 percent. First bank keeps $ 200 of the $ 1,000 in deposit in reserve and lends out the remaining $ 800.
Notice the first bank increases the supply of money by $800 when it makes loan. Before loan is made, the money supply is $1,000, equal to the deposits in first bank. After the loan is made, the money supply is $ 1,800. The depositor still has a demand deposit of $1000, but now the borrower holds $800 in currency. Thus, in a system of factional-reserve, banking, banks create money.
The creation of money does not stop with first bank. If the borrower deposits the $ 800 in another bank, the process of money creation continues. Here is the balance sheet of the second bank.

Second bank receive the $ 800 in deposits, keeps 20 percent, or $ 160, in reserve, and then loans out $ 640. Thus second bank creates $ 640 of money. If this $ 640 is eventually deposited in third bank, this bank keeps 20 percent, or 128, in reserve and loans out $512, resulting in this balance sheet.

The process goes on and on. With each deposit and loan, more money is created.
Reserve-deposit ratio refers to the fraction of deposit in reserve. In a system of fractional reserve banking, banks create money.
Although this process of creation can continue forever, it does not create an infinite amount of money. Letting rrdenote the reserve-deposit ratio, the amount of money that the original $ 1,000 creates is


Note
- The banking system’s ability to create money is the primary difference between banks and other financial institutions.
- Financial markets have the important function of transferring the economy’s resources from those households that wish to save some of their income for the future to those households and firms that wish to borrow to buy investment goods to use in their
production. - Financial intermediation is the process of transferring funds from savers to borrowers. Many institutions in the economy act as financial intermediaries; the most prominent examples are the stock market, the bond market, and the banking system. Yet, of these financial institutions, only banks have the legal authority to create assets that are part of the money supply, such as checking accounts. Therefore, banks are the only financial institutions that directly influence the money supply. Although the system of fractional reserve banking creates money. It does not create wealth.
When a bank loans out some of it reserves, it gives borrowers the ability to make transactions and therefore increase the supply of money. The borrowers are also under the obligation to the bank, however, so the loan does not make them wealthier. In other words, the creation of money by the banking system increases the economy’s liquidity, not its wealth.
3.2.3 A model of the money supply
What determines the money supply? Here is the presentation of a model of the money supply under fractional-reserve banking. The model has three exogenous variables
- The monetary base (B) which is the total dollars held by the public as currency on the hand (C) and by banks as reserves (R). This is directly controlled by the central bank/federal reserve.
- The reserve-deposit ratio (rr) –this is the fraction of deposits that banks hold in reserve. This is determined by the business policies of banks and the law regulating banks.
- The currency-deposit ratio (cr) –this is the amount of currency in hands (C) people hold as a fraction of their holdings of demand deposit (D). It reflects the preferences of households about the form of money they wish to hold.
The model shows how the money supply depends on the monetary base, the reserve-deposit ratio, and the currency-deposit ratio. It helps us examine how fed reserve/central bank policy and the choices of banks and households influence the money supply.


This equation shows how the money supply depends on the three exogenous variables. We can see that the money supply is proportional to the monetary base. The factor of proportionality, (cr+1)/(cr+rr), is denoted by m and is called the money multiplier
We can write
M=m x B
Each dollar of the monetary base produces m dollar of money. Because the monetary base has a multiplied effect on the money supply, the monetary base is sometimes called high-powered money.
The numerical example below, approximately describes a hypothetical economy. Suppose that the monetary base (B) is $ 500 billion, the reserve deposit ratio (rr) is 0.1, and the currency deposit ratio (cr) is 0.6. In this case, the money multiplier is
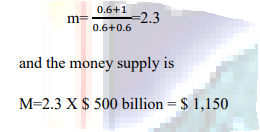
Each dollar of the monetary base generates 2.3 dollars of money, so the total money supply is $1,150 billion,
Note
- The money supply is proportional to the monetary base, thus, an increase in the monetary base increase the money supply by the same percentage.
- The lower the reserve-deposit ratio, the more loans banks make, and the more money banks create from every dollar of reserves. Thus a decrease in the reserve deposit ratio raises the money multiplier & the money supply.
- The lower the currency-deposit ratio, the fewer dollars of the monetary base the public holds as reserves, and the more base dollars banks can create. Thus, a decrease in the currency-deposit ratio raise the money the money multiplier and the money supply.
