
UNIVERSITY EXAMINATIONS: 2011/2012
EXAMINATION FOR THE CERTIFICATE IN BRIDGING MATHEMATICS
MAT 104 PROBABILITY AND STATISTICS
DATE: APRIL 2012 TIME: 1½ HOURS
INSTRUCTIONS: Answer Question One and Any other Two Questions
QUESTION ONE (COMPULSORY – 30 marks)
a) Define the following terms:
i) sample space
ii) Discrete variable
iii) Conditional probability. (3 marks)
b) A basket contains 7 mangoes and 3 apples. Three fruits are chosen at random, one at a time and is
not replaced.
i) what is the probability that all are mangoes (3 marks)
ii) What is the probability that two are mangoes (3 marks)
iii) What is the probability that at least one apple is chosen (3 marks)
c) Given the following set of discrete data: 42, 45, 47, 48, 48, 52, 52, 54, 55. Calculate mode, median,
mean and semi-interquartile range (7 marks)
d) The table below gives a probability distribution of a discrete random variable X. Given that
P(X<13) = 0.75. Find value of v and w; hence calculate E(X) and P(X>9). (9 marks)
X 4 8 12 15 20
P(X) v 0.25 0.3 w 0.1
e) Suppose that A and B are events defined on sample space S. Explain the following
i) A and B are mutually exclusive
ii)A and B are independent (2 marks)
QUESTION TWO
a) The following data gives the monthly earnings in dollars of some casual employees.
132, 148, 148, 139, 142, 128, 135, 136, 140, 133, 126
136, 142, 134 , 144 , 139 , 134, 135, 132, 126, 139, 128
i) starting with 126 as the LCL of the first class and using the 2k > n rule to select the number of
classes k, organize the data into grouped frequency distribution table (5 marks)
ii) Using an appropriate Assumed Mean estimate the mean and standard deviation of the data.
(6 marks)
b) Past records show that 70% of CBM students pass the certificate examination. If a group of eight
students is selected at random from former CBM students, what is the probability that;
i) Three passed the examination (2 marks)
ii) At least one failed the examination (2 marks)
QUESTION THREE
a) Find the value of x for the following data whose mean is x hence or otherwise determine its
standard deviation and seventh decile; (8 marks)
16, 7, 3, 18, 8, x+1, 10, 14
b) let S and T be two events in a random experiment with probabilities P(S) = 0.68 and P(T) = 0.55.
(4 marks)
i) Find the probability that either S or T occurs if the two events are independent
ii)Find the probability that either S or T occurs if the two events are mutually exclusive.
c) Three high schools had 30, 25 and n candidates in KCSE respectively last year. Their mean score in
points were 8.5, 7.4 and 6.2 respectively. If their combined mean score was 7.3, find the value of n.
(3 marks)
QUESTION FOUR
a) A number is randomly selected from all the odd integers between 1 and 25 inclusive. Let A be the
event that the number is divisible by 3 and B be the event that the number is divisible by 5.
i) Represent this information in a venn diagram (2 marks)
ii) Find P(A) and P(B′) (2 marks)
iii) Find P(A∪ B), P(A∩ B) and P(A∩ B′ ) (3 marks)
b) For a certain sample of size 20 collected on a random variable X,
∑x = 180 and ∑ = 2080 2x
i. find the mean and standard deviation of the sample (3 marks)
ii. redo (i) after dropping 10 which was one of the sample values (3 marks)
iii. write down the answers to (i) if each value is increased by 5 (2 marks)
QUESTION FIVE
a)The probability that it will be cloudy today in Nairobi is 0.24, if it is cloudy the probability that it
rains is 0.82. if it is not cloudy the probability that it rains is 0.22. Find the probability that it does
not rain today in Nairobi. (3marks)
b) The table below shows the cost, in Kenya Shillings of breakfast items and the corresponding
weights in supermarkets A and B.
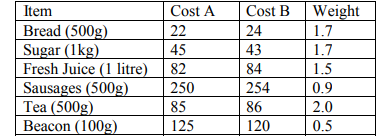
Taking supermarket A to be the base, calculate the composite index for the cost of breakfast items and
interpret your result. (4 marks)
c)A set of data, X and Y gave the following summary,
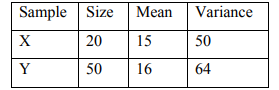
i) Find the combined mean for the data (3 marks)
ii) Suppose the two data were converted to new data by first multiplying by 2 and then adding 5 to
the result. Find the combined mean of the new data. (2 marks)
d) A fair coin is tossed 10 times. Use the binomial formula to find the probability of obtaining at least
two heads. (3 marks)
