
MAASAI MARA UNIVERSITY
REGULAR UNIVERSITY EXAMINATIONS
2015/2016 ACADEMIC YEAR
FIRST YEAR SECOND SEMESTER
SCHOOL OF BUSINESS & ECONOMICS
COMMON COURSE
COURSE CODE: IRD 104
COURSE TITLE: QUANTITATIVE SKILLS II
DATE: 6TH MAY, 2016 TIME: 2.30 – 4.30PM
INSTRUCTIONS TO CANDIDATES
Answer Question ONE and any other THREE questions
Mobile phones are not allowed in the exam room
No writing on the question paper
This paper consists of 2 printed pages. Please turn over.
Briefly explain the meaning of the following terms
Regression analysis and correlation
Discrete random variable and continuous random variable
Alternative hypothesis and null
Point estimate and interval estimate
Skewness and kurtosis (5marks)
It is known that from a lot of 100 computers there are 20 defective ones. 5 of these computers are selected at random and tested. Find the probability that only 2 of the 5 are defective (3marks)
On the basis of the results obtained from a random sample of 100 men from Narok County the 95 % confidence interval for the mean height of the men in the district is found to be (177.22cm,179.18cm)
Find the value of X ̅ , the mean of the sample and ? the standard deviation of the normal population from which the sample is drawn. (3 marks)
Construct/calculate the 98% confidence interval for the mean height (2 marks)
A random sample of 12 items taken from a normal population gave the following data X ̅=82,∑▒X^2 =686,800
Find the 95% confidence intervals for the population mean. (2 marks)
In a competitive examination of 5000 students, the marks of the examinees in statistics were found to be distributed normally with mean 45 and standard deviation 14. Determine the number of examinees whose marks out of 100 were
Less than 30 (1 mark)
Between 30 and 70 (2 marks)
More than 40 (1 mark)
The demand and price (in Ksh ‘000’) for a bag of a hybrid 100kg bag of wheat in different regions of the country is as shown below
Price (in Ksh ‘000’) 7 9 8 11 13 12
Demand 24 28 25 30 31 30
Calculate the Pearson correlation coefficient and comment on your answer. (6marks)
QUESTION TWO (15 MARKS)
In an assembly plant the number of units produced in a day is believed to depend on the number of workers present and the number of hours they work. The following data was collected

Find the estimated regression line of Y on X_1and X_2 (11 marks)
Predict the number of units that would be produced if 8 workers worked for 8 hours (4marks)
QUESTION THREE (15 MARKS)
In a large manufacturing company an opinion survey was conducted regarding two types of bonus schemes. Total employees were divided into two categories, namely: laborers and executives. The results obtained by way of opinion survey are presented in the form of contingency table as given below.

Test at α= 5%, whether the opinion about bonus schemes is independent of the types of employees (10 marks)
A shop sells a particular make of radio at a rate of 4 per week on average. The number sold in a week has a Poisson distribution.
Find the probability that the shop sells at least 2 in a week (2marks)
Find the probability that the shop does not make any sale in a week (3marks)
QUESTION FOUR (15 MARKS)
Given the following data
X 1 2 3 4 5 6 7 8 9 10
Y 1 4 8 14 14 17 20 22 26 30
Fit a regression line of Y on X
Find the value of Y when X=3.5 (10 marks)
For a given se of data, the observed and expected frequencies are shown.
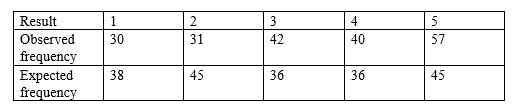
Are the differences between the observed and the expected frequencies significant at 1% level? (5 marks)
QUESTION FIVE (15 MARKS)
State the errors committed when
A null hypothesis is rejected when it ought to be accepted (1 mark)
A null hypothesis is accepted when it ought to be rejected (1 mark)
The prices of shares of a company on different days in a month were found to be
66, 65, 69, 70, 69, 71, 70, 63, 64 and 68.
Discuss whether the mean price of the shares in the month is 65 at α=5%
(7 marks)
Assuming that the sample came from a normal population with variance 4, calculate a 95% confidence interval for the mean length of all the worms in the garden. (3 marks)
The mean monthly income of 144 casual workers in a certain county is 5000 with a standard deviation of 1200. Test the hypothesis that the monthly income of these casual workers is 5500 (use α=0.05) (3marks)
