
MAASAI MARA UNIVERSITY
REGULAR UNIVERSITY EXAMINATIONS
2018/2019 ACADEMIC YEAR
THIRD YEAR SECOND SEMESTER
SCHOOL OF BUSINESS & ECONOMICS
BACHELOR OF SCIENCE IN INFORMATION SCIENCE
COURSE CODE: INS 3203
COURSE TITLE: QUANTITATIVE METHODS
FOR INFORMATION SCIENTISTS
DATE: 15TH APRIL 2019 TIME: 0830AM -10.30AM
INSTRUCTIONS TO CANDIDATES
i. Answer question ONE and any other THREE questions
ii. Do not write on the question paper
iii. Use illustration and diagrams where they serve to support the answers.
This paper consists of 4 printed pages. Please turn over
INS 3203: Quantitative Techniques for Information Scientists Page 2
QUESTION ONE (25 MARKS)
a) Explain each of the following
i) Conditional probability (3 marks)
ii) Collectively exhaustive events (3 marks)
b) Give the probability of each of the following :
i) A or B when the two events are not mutually exclusive (2 marks)
ii) A and B when the two events are dependent (2 marks)
c) Find the probability of tossing a coin and getting a tail then rolling a six sided die and
obtaining less than four (5 marks)
d) A blood bank catalogs the types of blood including positive or negative. Rh-factor given
by the donors during the blood donation week. The number of donors who give each
blood type in your college is listed in the following table.

Required : find the probability that the donor has
i. Type A or B blood (3 marks)
ii. Type AB and is Rh-positive (3 marks)
iii. Type B given that the donor is Rh- negative (4 marks)
INS 3203: Quantitative Techniques for Information Scientists Page 3
QUESTION TWO (15 MARKS)
a) Show that the compounding interest amount at the end of n period (An) equal to
Ai(1+i)
n-1
(4 marks)
b) John has undertaken to invert Ksh. 200,000 with a given financial institution at an
interest rate of 8% per annum.
i) If the interest is paid into the account on a monthly basis, determine the
amount accrued in the investment after six years (4 marks)
ii) Assume that the interest is for the same investment paid daily. Determine
what amount will accrue after the six years period (3 marks)
c) Given an investment that offers interest of 10% per annum over a period of seven
years. Determine the amount you would need to invest now in order to accrue Ksh.
500,000 at the end of the seven year period. (4 marks)
QUESTION THREE (15 MARKS)
In a recent report a magazine suggested that the typical family of four with an intermediate
budget spends an equivalent of Ksh. 9600 per week on food. The following frequency
distribution was included as part of the report.
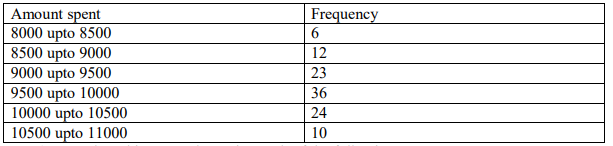
a) Based on this report determine each of the following
i) The variance (3 marks)
ii) The standard deviation (1 marks)
iii) The Karl Pearson’s coefficient of variation (2 marks)
b) A recent study of the hourly wages of maintenance crews for major airlines showed
that the mean after tax hourly earning was Ksh. 2,550 with a standard deviation of
Ksh. 450. If we select a crew member at random. What is the probability this crew
member earns
i. Between Ksh.2000 and Ksh. 2900 (3 marks)
ii. Less than Ksh. 2,400 (3 marks)
iii. Between Ksh. 1,900and Ksh. 2,300 (3marks)
If α = 0.05
INS 3203: Quantitative Techniques for Information Scientists Page 4
QUESTION FOUR (15 MARKS)
a) Explain what is meant by skewness as applied to the study of statistics
diagrammatically explaining the different types of skewness (5 marks)
b) Given the distribution as 1,2,3,4,5 determine the coefficient of skewness using the
statistical software approach and comment on the shape of the data (5 marks)
c) Explain what is meant by Kurtosis explaining the different types of Kurtosis
(5 marks)
QUESTION FIVE (15 MARKS)
Given the data of daily production of trans receivers at Nairobi electrics organized in
a distribution table as below
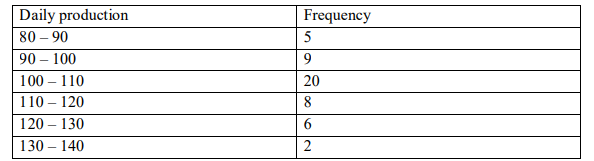
Estimate each of the following
i) The mean (3 marks)
ii) The median (4 marks)
iii) The mode (4 marks)
iv) The interquartile range (4 marks)
