TUESDAY: 5 April 2022. Morning paper. Time Allowed: 3 hours.
Answer ALL questions. Marks allocated to each question are shown at the end of the question. Show ALL your workings. Do NOT write anything on this paper.
QUESTION ONE
1. Using suitable illustrations, define the following matrices:
Identity matrix. (3 marks)
Diagonal matrix. (3 marks)
Null matrix. (3 marks)
2. A wholesaler sold 30 cartons of milk and 20 crates of bread for Sh.31,000. He later sold 40 cartons of milk and 10 crates of bread for Sh.28,000.
Required:
- Formulate simultaneous equations to represent the above information. (2 marks)
- Using matrix algebra, determine the price of a carton of milk and the price of a crate of bread. (7 marks)
- The amount the wholesaler could earn if he sold 50 cartons of milk and 30 crates of bread? (2 marks)
(Total: 20 marks)
QUESTION TWO
1. Consider the functions below for X Ltd.:
TR = 40q — 10q2
TC = – 2q2 + 4q + 10
Where:
TR is the total revenue TC is the total cost
q is the number of units produced and sold
Required:
The total profit function. (4 marks)
The profit maximising units. (4 marks)
The maximum profit. (3 marks)
2. The table below shows the prices and quantities of four beauty products used in a salon for the years 2020 and 2021:
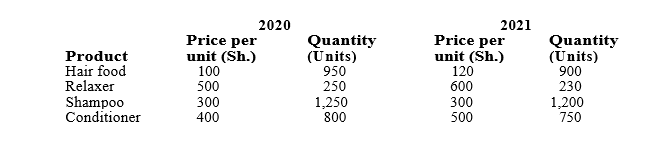
Required:
Laspeyre’s price index using 2020 as the base year. (3 marks)
Paashe’s price index using 2020 as the base year. (3 marks)
Marshall’s Edge-worth price index. (3 marks)
(Total: 20 marks)
QUESTION THREE
- Highlight five advantages of probability sampling. (5 marks)
- Eliud Kimani deposited Sh.390,000 into a bank account which earned interest at the rate of 14% per annum compounded quarterly. He withdrew Sh.470,000 from the account after five years. He intends to purchase a farm machinery worth Sh.800,000 after another two years.
Required:
The amount of money Mr. Kimani needs to deposit in the account to enable him purchase the machinery in two years’ time. (6 marks)
3. A Kenyan businessman imported 380 bicycles from Finland at a cost of 455 Euros (€) per bicycle and 120 lorries from Switzerland at a cost of 950 Swiss Franc (SFr) per lorry.
He incurred the following additional expenses:
- 12% on cost for custom duty
- 5% on cost for insurance
Shipment fee on bicycles at Ksh.400,000 while shipment fee on lorries at Ksh.600,000.
The exchange rates prevailing at the time were:
1 Euro (€) = Ksh.140
1 Swiss Frac (SFr) = Ksh.90
1 US Dollar ($) = Ksh.108
Required:
The total cost of the consignment in US Dollars ($). (5 marks)
The selling price per bicycle and lorry if the profit is 20% and 25% on cost respectively. (4 marks)
(Total: 20 marks)
QUESTION FOUR
1. Highlight two advantages and two disadvantages of the interview method of collecting primary data. (4 marks)
2. Outline the dependent and independent variables for each of the following graphical representations:
Histogram. (2 marks)
Lorenz curve. (2 marks)
Ogive curve. (2 marks)
3. The table below shows the salaries earned by employees of XYZ Ltd. in a given month:
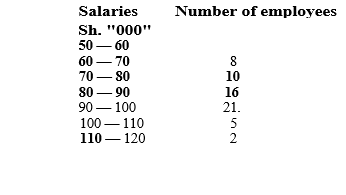
Required:
The average salary. (3 marks)
The upper Quartile (Q3) of salary distribution. (3 marks)
The standard deviation of the salary distribution. (4 marks)
(Total: 20 marks)
QUESTION FIVE
1. Njimbi town has 700 households. Each household has a preference of either cooking gas brand A, B C or none as summarised below:
400 households prefer Brand A.
350 households prefer Brand B.
470 households prefer Brand C.
250 households prefer Brands A and C. 140 households prefer Brands A and B. 200 households prefer Brands B and C.
50 households do not prefer any of the three brands.
Required:
Present the above information in a Venn diagram. (5 marks)
The number of households that prefer all the three brands. (4 marks)
The number of households that prefer only one brand. (2 marks)
2. A, B and C are three football teams. The probability of team A, B and C winning a game is %, 3/4 and 2/7 respectively.
Required:
Represent the above information in a tree diagram. (4 marks)
The probability of only one team winning the game. (3 marks)
The probability of all three teams winning the game. (2 marks)
(Total: 20 marks)
