
UNIVERSITY EXAMINATIONS: 2016/2017
EXAMINATION FOR THE DEGREE IN BACHELOR OF
SCIENCE IN INFORMATION TECHNOLOGY/
BACHELOR OF BUSINESS INFORMATION TECHNOLOGY/
BIT2102 BIT 3101A BBIT 106 DATA STRUCTURES AND
ALGORITHMS
MODE: FULL TIME/PART TIME/DISTANCE LEARNING
ORDINARY EXAMINATIONS
DATE: AUGUST, 2017 DURATION: 2 HOURS
INSTRUCTIONS: Answer question ONE and any other TWO questions
QUESTION ONE [30 MARKS]
a) Differentiate between the following concepts as used in algorithm analysis.
i. Space complexity and time complexity
ii. Big O notation and theta notation
[4 Marks]
b) If you push the letters D, C, B and A in order onto a stack of characters and then pop
them, in what order will they be deleted from the stack?
[4 Marks]
c) Define a recursive function and give any two examples that can be solved recursively.
[4 Marks]
d) The numbers 20, 70, 68, 59,30,15,90,70,60,85 are to be stored for some processing in
that order. Write down the order in which the numbers will be printed if they are:
i. stored in a queue
ii. stored in a stack and
iii. stored in a binary search tree and traversed in order.
[9 Marks]
e) Explain the sufficient conditions for a binary tree to be a heap.
[2 Marks]
f) Design an algorithm for calculating Fibonacci series and estimate its big O.
[7 Marks]
QUESTION TWO [20 MARKS]
a) Write down the algorithm for merge sort and state its big O.
[6 Marks]
b) Performing operations such as delete and insert in a doubly linked list is not easy.
Explain.
[4 Marks]
c) Explain how the divide and conquer technique works. Give two examples.
[4 Marks]
d) Represent the following expression tree: (((A+B)*C+D)*E)-((A+B)*C-D) and write
the prefix and postfix expressions.
[6 Marks]
QUESTION THREE [20 MARKS]
a) Distinguish between preorder and postorder traversal of a binary tree
[4 Marks]
b) Consider the following of a table fields, construct a binary tree to represent them.

[4 Marks]
c) Describe two applications of binary search trees.
[2 Marks]
d) ) Explain why a queue is a two-point structure where a stack is one point structure
[3 Marks]
e) What is an algorithm?
[2 Marks]
f) Describe the following properties that an algorithm must have: precision, uniqueness,
finiteness, input and output.
[5 Marks]
QUESTION FOUR [20 MARKS]
a) Explain what is an in-order traversal for a binary tree?
[2 Marks]
b) Write an algorithm to execute an in-order traversal.
[3 Marks]
c) Estimate the order of magnitude for the expression
[4 Marks]
d) Describe two ways of representing a graph ADT.
[4 Marks]
e) Construct a directed graph with the vertices A,B,C,D and E using the information
below.
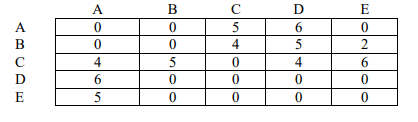
[5 Marks]
f) Briefly describe the depth first search algorithm as used in graph traversal.
[2 Marks]
QUESTION FIVE [20 MARKS]
a) If two or more values in a hash function, map to the same key, a collision is said to
occur. Collisions are not allowed in a hash table. Briefly describe the following
techniques for resolving collisions.
i. re-hashing
ii. chaining
iii. linear probing.
[6 Marks]
b) Differentiate between dynamic programming and backtracking algorithms. Give one
example for each.
[4 Marks]
c) Describe the guidelines for developing an algorithm using a pseudo code.
[5 Marks]
d) Describe the procedure for insert sort.
[3 Marks]
e) Re-arrange the following numbers in descending order using insert sort.
2,4,8,6,10,16,12,14,20,18.
[2 Marks]
