
UNIVERSITY EXAMINATIONS: 2018/2019
EXAMINATION FOR THE DEGREE OF BACHELOR OF SCIENCE IN
INFORMATION TECHNOLOGY /BACHELOR OF BUSINESS IN
INFORMATION TECHNOLOGY / BACHELOR OF SCIENCE IN
APPLIED COMPUTING
BIT1301 BUSS202 PROBABILITY AND STATISTICS
FULL TIME/PART TIME/DISTANCE LEARNING
DATE: APRIL, 2019 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions.
QUESTION ONE [30 MARKS]
(a)Using a suitable diagram, state the difference between Skewness and kurtosis. (4 Marks)
(b) Find the coefficient of variation of a frequency distribution given that the mean is 120, mode is 123
and Karl Pearson’s coefficient of skewness is -0.3. (3Marks)
(c) A bag contains 3 red balls and a number of black ones. The probability of drawing a red ball from the
bag is 0.2. How many balls are there in the bag? (2Marks)
(d)The table below shows the performance of various drivers in a car rally.
Drivers name Accumulated points Distance covered (km)
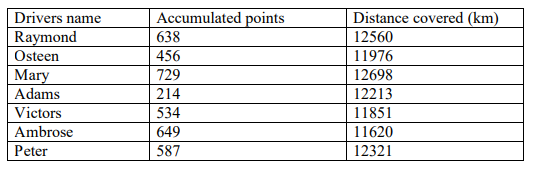
Determine the rank correlation coefficient for this information and interpret it
(6Marks)
(e) 5% of all TVS manufactured by a large electronic company are defective; a quality control
inspector randomly selected three TV’s from the production line. What is the probability that
exactly one of these three TV’s is defective? (4 Marks)
(f) List two properties of the normal distribution. (2 Marks)
(g) In a nationwide survey,100 boys and 50 girls are sampled. For boys, the average number of
absences in the first year is 15 with a standard deviation of 7.; for girls, the average number of
absences is 10 with a standard deviation of 6. What is the mean and standard deviation of
absences for the entire group of 150 students. (4 Marks)
(h) Five students attained the following Marks in Statistics examination.
62,57,45,72and 64 calculate the standard deviation and the interquartile range. (5 Marks)
QUESTION TWO (20 MARKS)
(a) Distinguish between ‘correlation ‘and ‘regression’. (4Marks)
(b) For a period of three years an IT company monitors the number of units of output per quarter and
the total cost of producing the units. The table below shows their results.
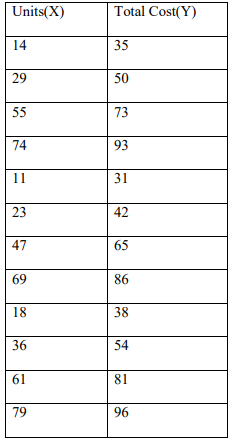
(a) Draw a scatter diagram for the data and interpret it. (4Marks)
(b) (i) Calculate the equation of the regression line of y on x. (7Marks)
(ii) Draw this line on your scatter diagram. (3Marks)
(c) Estimate the total cost when X=52 units. (2Marks)
QUESTION THREE (20MARKS)
(a) If 10% of items produced turn out to be defective,then find out the probability that out of 10
randomly selected items there are:
(i) Exactly three that are defective (3 Marks)
(ii) At least two that are defective (3 Marks)
(iii) More than eight are defective (4Marks)
(b) The number of passengers in a car in a freeway has the probability mass function given by
Number of

(i) Does the distribution meet the two requirements for probability distribution of a
discrete random variable? Justify your answer. (3Marks)
(ii) Find the expected number of passengers in a car. (3Marks)
(iii) Calculate the standard deviation of the number of passengers in a car. (4Marks)
QUESTION FOUR (20MARKS)
(a) Given below are the daily wages paid to workers in two factories X and Y.
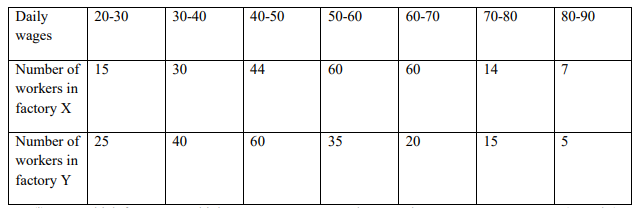
(i) Which factory pays higher average wages? By how much? (5Marks)
(ii) In which factory are the wages more variable? (5Marks)
(iii) Which factory has to pay more wages in a month assuming that both work for 25 days in a
month? (5Marks)
(b) If the probability that a husband will be alive in 50 years is 0.4 and the probability that the wife will be
in 50 years is 0.7. Find the probability that
(i) Both will be alive. (2Marks)
(ii) None will be alive (3Marks)
QUESTION FIVE (20 MARKS)
(a)Suppose that the total pre-tax profit of IT companies in region ABC is known to be normal
with mean Ksh. 100 million and a standard deviation of Ksh. 80million.Determine
(i) The probability that one of these companies has a pre-tax profit of at most 200million.
(ii) The probability that one of these companies has a pre-tax profit of at least 70 million.
(iii)The number of companies out of 50 that will have a pre-tax of at least 110million.
(10 Marks)
(b) The median and the mode of the following distribution are known to be 27 and 26 respectively.

(i) Show that the values of a and b are 8 and 7 respectively. (5 Marks)
(ii) Compute the arithmetic mean and the standard deviation of the distribution. (5 Marks)
