
UNIVERSITY EXAMINATIONS 2017/2018
ORDINARY EXAMINATION FOR BACHELOR OF SCIENCE INFORMATION
TECHNOLOGY, BSc. APPLIED COMPUTING
BIT 1206: DISCRETE MATHEMATICS (DAY/EVENING)
DATE: DECEMBER 2018 TIME: 2 HOURS
INSTRUCTIONS: Answer question ONE and Any other TWO questions
QUESTION ONE
a) Find the sum of products for the function ?(?, ?, ?) = (? + ?)?̅ using
Boolean identities (4 Marks)
b) Find the positive integer ? such that 10 C n =
10 C n + 2 (6 Marks)
c) i) Distinguish between a multigraph and a pseudograph. (2 Marks)
ii) How many edges are there in a graph with 10 vertices each of degree six? (2 Marks)
d) Consider the directed graph G below
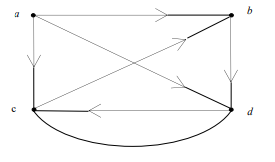
i) Find the indegree and outdegree of each vertex (2 Marks)
ii) Find the successor list of each vertex G (2 Marks)
iii) Are there any sources or sinks? (2 Marks)
e) Solve the following linear homogeneous recurrence relation:
?? = 4 ??−1 – 4 ??−2 with initial conditions
?0 = 4
?1 = 12 (2 Marks)
2
f) Given the Sets:
A = {3, 5, 7, 8, 11, 12}
B = {2, 5, 6, 8, 10, 12}
Determine A ∩ B (2 Marks)
g) Show that p ˄ q logically implies p ↔ q (3 Marks)
h) Consider a graph where
V (G) = {A, B, C,D} and
E (G) = [{A, B,}, {B, C}, {B,D}, {C,D}]
Find the degree and parity of each vertex in G (3 Marks)
TOTAL: [30 MARKS]
QUESTION TWO
a) Draw the multigraph G whose adjacency matrix A is A =
b) Let G be the graph where
V (G) = {A, B, C, X, Y, Z} and
E (G) = [{A, C}, {A, X}, {A, Y}, {B, Y}, {B, Z}]
i) Find G-A (3 Marks)
ii) Determine the number of connected paths of G-A (3 Marks)
c) Draw the Diagrams of each of the following graphs G (V,E):
i) V = {A,B,C,D}
ii) E = [{A,B},{A,D},{B,C},{B,D}{C,D}] (3 Marks)
iii) V= {a, b, c, d, e}
iv) E= [{a, b}, {a, c}, {b, c}, {d, e}] (3 Marks)
d) Order the sets of numbers: Z, IR,QI , IN using ⊂ (3 Marks)
e) Consider the propositions:
p: Juan is a math major.
f: Juan is a computer science major.
Use symbolic connectives to represent the proposition “Juan is a math major but not a
computer science major.” (3 Marks)
TOTAL [20 MARKS]
QUESTION THREE
a) Define the following terms
i) One-to-one (or injective ) Functions (2 Marks)
ii) Onto (or surjective) Functions (1 Mark)
iii) One-to-one correspondence (or bijective) Functions (2 Marks)
iv) Invertible Functions (2 Marks)
b) Let A=
a,b,c,d,e
and B be the set of letters in the alphabet. Let the functions f, g and h
from A into B be defined as follows:
f g h
a → z a → z a → z
b → a b → y b → c
c → s c → x c → e
d → r d → y d → r
e → e e → z e → s
Are any of these functions one to one? (2 Marks)
c) Consider the functions
f(x) = 2x − 3 and g(x) = x
2 + 3x + 5
Find a formula for the composition functions:
i) g ∘ f (1 Mark)
ii) f ∘ g (2 Mark)
d) Consider the maps
f ∶ A → B, g ∶ B → A
h ∶ C → B, F: B → C
G ∶ A → C
i) Is g∘f defined? If so what is the domain and codomain? (2 Marks)
ii) Is h∘f defined? If so what is the domain and codomain? (2 Marks)
iii) Is F∘h∘G defined? If so what is the domain and codomain? (2 Marks)
Is G∘F∘h defined? If so what is the domain and codomain? (2 Marks)
TOTAL: [20 MARKS]
QUESTION FOUR
a) List the elements of the following sets
i) A = {x: x ∈ N, 3 < ? < 9} (1 Mark)
ii) B = {x: x ∈ N, x
2 + 1 = 10} (1 Mark)
iii) C = {x: x ∈ N, x is odd , −5 < ? < 5} ` (1 Mark)
b) (i) Draw a Venn diagram of sets A, B, C where A ⊆ B, sets A and C are disjoint
but B and C have elements in common (4 Marks)
(ii) Write A ∩ (B ∪ C) as the (disjoint) union of fundamental products. (5 Marks)
c) A survey on a sample of 25 new cars being sold at a local auto dealer was conducted to see which
of the three popular options, air-conditioning (A), radio(R), and power windows (W) were
already installed. The survey found:
15 had air-conditioning
12 had Radio
5 had air-conditioning and Power windows
9 had air-conditioning and radio
4 had radio and power window
3 had all the three options
2 had no options
Find the number of cars that had:
i) Only power windows (2 Marks)
ii) Only air-conditioning (1 Mark)
iii) Only radio (1 Mark)
iv) Radio and power windows but not air-conditioning (1 Mark)
v) Air conditioning and radio but not power windows (1 Mark)
vi) Only one of the options (2 Marks)
TOTAL: [20 MARKS]
QUESTION FIVE
(a) How many committees of five with a given chairperson can be selected from twelve persons?
(5 Marks)
(b) How many diagonals has a regular polygon with n sides (5 Marks)
(c) Which regular polygon has the same number of diagonals as sides (5 Marks)
(d) Prove P(n,r) =
?!
(?−?)!
= ?(? − 1)(? − 2) … . . (? − ? + 1) (5 Marks)
TOTAL: [20 MARKS]
