UNIVERSITY EXAMINATIONS: 2011/2012
UNIVERSITY EXAMINATIONS: 2011/2012
FIRST YEAR EXAMINATION FOR THE BACHELOR OF SCIENCE
IN INFORMATION TECHNOLOGY
BIT 1301 PROBILITY AND STATISTICS
DATE: JULY, 2012 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE
a) Define the following terms giving appropriate examples in each case.
i. Mutually exclusive events. (1 Mark)
ii. A sample space. (1 Mark)
iii. Discrete random variable (1 Mark)
iv. Continuous random variable (1 Mark)
v. Qualitative data (1 Mark)
b) State the two basic properties of probability density function (pdf) for a
continuous random variable. (2 Marks)
c) The data below represents masses to the nearest kilogram of fish caught in a day.
Masses 5 – 9 10 – 14 15 – 19 20 -24 25 – 29
No. of fish 5 20 10 10 5
Determine:
i. Mean (4 Marks)
ii. Mode (4 Marks)
iii. Median (4 Marks)
d) If x has the probability density function
{ (1 ), 0 1 ( ) 0,
kx x f x elsewhere
− ≤≤ =
Find k and P x (0.5 1) ≤ ≤
(4 Marks)
e) A random variable X has the following probability distribution table
X 0 1 2 3 4 5 6 7
P(X) 0 k 2k 2k 3k K2 2k2 7k2
+k
i. Find the value of k. (4 Marks)
ii. Evaluate P(X≤ 6). (3 Marks)
QUESTION TWO
a) i. Define a binomial random variable and state the four conditions
of a binomial experiment. (5 Marks)
ii. Find the probability of getting 98 heads in 200 tosses of a fair coin.
(3 Marks)
b) A police department consists of 25 officers of whom 5 are from the marginalized
areas. Three officers are selected to meet with the mayor. Find the probability that
i. None of the officers selected to meet the mayor comes from the marginalized
areas. (3 Marks)
ii. All the three officers selected to meet the mayor comes from marginalized areas.
(3 Marks)
c) i. State the Bayes theorem (2 Marks)
ii. In a bolt factory, machine A manufacture 45% of the total bolts while B
55% . Of their output, 5 % from A and 4 % from B are defective. A bolt is
drawn at random from the output and it is found to be defective. What is
the probability that it was manufactured by machine B. (4 Marks)
QUESTION THREE
a) i. Find the regression line of y on x for the following data. (6 Marks)
x 14 15 12 13 14 14
y 15 15 16 15 16 15
ii. Using the table above estimate the value of y when x = 10 (2 Marks)
b) 160 students scored the following marks in a statistics examination
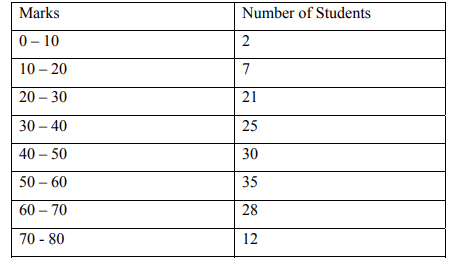
Compute the following:
i. The inter quartile range (4 Marks)
ii. 40th percentile (4 Marks)
iii. 3rd decile (4 Marks)
QUESTION FOUR
a) The random variable and probability distribution function define a model of an
investment process as follows.
Probability distribution function for investment project returns
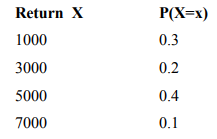
Determine:
i. The mean / expected value (4 Marks)
ii. The variance for the discrete random variable (4 Marks)
b) Consider a continuous random variable X with its probability density function
given by:
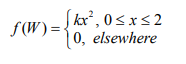
i. The value of (3 Marks)
ii. The mean of (4 Marks)
iii. The variance of X (5 Marks)
QUESTION FIVE
a) Students of a class were given an aptitude test. Their marks were found to be
normally distributed with mean of 60 and standard deviation of 5.
What percentage of the students scored more than 60 marks? (4 Marks)
b) A coin is tossed 3 times, draw a tree diagram to show the possible sample space
and estimate the probability of getting
i. Three heads.
ii. Two heads and a tail.
iii. At least 2 tails (6 Marks)
c) A manufacturer intends that his electric bulbs have a life of 1000 hours. He tests a
sample of 20 bulbs drawn at random and discovers that the mean life of the
sample bulbs is 990 hours with a standard deviation of 22 hours. Does this signify
that the batch is not up to the standard? (5 Marks)
Value of t1 at 1% level of significance with 19 degrees of freedom is 2.539 from tables.
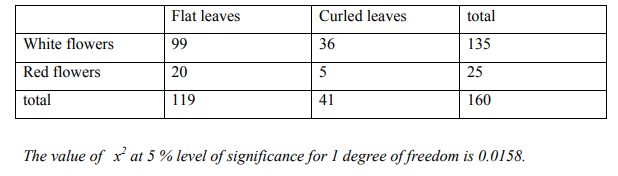
d) The following table shows the number of plants having certain characteristics.
Test the hypothesis that the flower colour is independent of flatness of leaf.
(5 Marks)