 UNIVERSITY EXAMINATIONS: 2011/2012
UNIVERSITY EXAMINATIONS: 2011/2012
FIRST YEAR EXAMINATION FOR THE BACHELOR OF SCIENCE
IN INFORMATION TECHNOLOGY
BIT 1206 DISCRETE MATHEMATICS
DATE: AUGUST, 2012 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE
a) In a survey of 100 students, the numbers studying the various languages were
found to be: Spanish 28, German 30, French 42, Spanish and German 8, Spanish
and French 10, German and French 5, all three languages 5.
i. How many were studying no language?
ii. How many had French as their only language?
(5 Marks)
b) Give the converse, contrapositive and inverse of the following implication: “ If it
rains today, l will go to college tomorrow”. (6 Marks)
c) Write the following statements in Symbolic form:
i. The sun is bright and the humidity is not high.
ii. If you do not see me tomorrow, it means l have gone to Chicago.
(4 Marks)
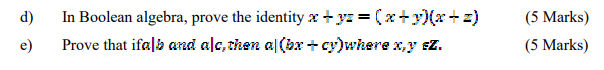

(5 Marks)
QUESTION TWO
a) Test the validity of the following argument. If two sides of a triangle are equal,
then the opposite angles are equal. Two sides of a triangle are not equal. The
opposite angles are not equal. (6 Marks)
b) Given the following propositions: p: food is good, q: service is good, r : restaurant
is 5 Star. Write the following in Symbolic notation:
i. Either food is good or the service is good or both
ii. Either food is good or service is good but not both
iii. Food is good while the service is poor
iv. It is not the case that food is good and the rating is five star
v. If both the food and the service are good, then the rating will be 5 Star.
vi. It is not true that 5 Star rating always means good food and good service.
(6 Marks)
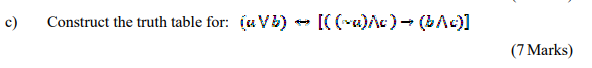
(7 Marks)
QUESTION THREE
a) Write the following statement in symbolic form: There will be no test
examination tomorrow if Professor is out of town or there’s a Matatu Strike.
(3 Marks)
b) Show that xy + yz + xz = xy + yz + xz (7 Marks)
c) Show that these identities hold:
i. x ⊕= + y x y xy ( )( )
ii. x ⊕= + y xy xy ( ) ( )
(4 Marks)
d) Translate the distributive law into logical equivalence and
prove. (8 Marks)
QUESTION FOUR
a) For each pair of integers a and b, find integers q and r such that
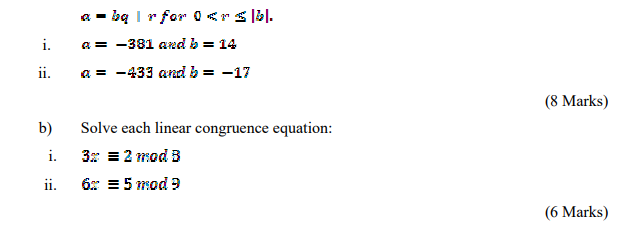
(6 Marks)
c) Find the smallest positive integer x such that when x is divided by 3 it yields a
remainder 2, when x is divided by 7 it yields a remainder 4, and when x is divided
by 10 it yields a remainder 6? (6 Marks)
QUESTION FIVE
a) Define the following terms as used in Graphs:
i. Directed Graph
ii. Degree of a vertex in a graph
iii. Path
iv. Connected graph
v. Subgraph.
b) Consider the graph G below:
(10 Marks)
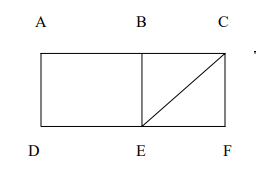
Find:
i. All simple paths from A toF
ii. All trails from A to F
iii. All cycle which include vertex A
iv. All cycles in G.
(10 Marks)
