 UNIVERSITY EXAMINATIONS: 2013/2014
UNIVERSITY EXAMINATIONS: 2013/2014
ORDINARY EXAMINATION FOR THE BACHELOR OF SCIENCE
IN INFORMATION TECHNOLOGY
BIT1301 PROBABILITY AND STATISTICS
DATE: APRIL, 2014 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE
a) The mean mass of a set of components is 750kg and the standard deviation is
50kg. Assuming the masses are normally distributed about the mean, determine
for a sample of 64 components, how many are likely to have masses of.
i. Less than 735kg. (3 Marks)
ii. Between 740 and 760kg. (4 Marks)
b) In a group of40people,10are healthy and every person of the remaining30haseither high blood pressure, a high level of cholesterol or both. If15have highblood pressure and25have high level of cholesterol:
i. How many people have high blood pressure and a high level of
cholesterol? (3 Marks)
ii. If a person is selected randomly from this group, what is the probability
that he or she has high blood
event A . (2 Marks)
iii. If a person is selected randomly from this group, what is the probability
that he or she has high level of cholesterol
event B . (2 Marks)
iv. If a person is selected randomly from this group, what is the probability
that he or she has high blood pressure and high level of
cholesterol
event Aand B . (2 Marks)
v. If a person is selected randomly from this group, what is the probability
that he or she has high blood pressure or high level of
cholesterol
event Aor B . (2 Marks)
vi. Use the above to check the probability formula: (3 Marks)
P AorB P A P B P Aand B .
c) An exploration firm finds that 5% of the test wells it drills yield a deposit of
natural gas. If the firm drills 6 wells, what is the probability that
i. Exactly 2 wells yield gas.
ii. At least 1 well yields gas.
iii. At most 3 wells yield gas.
(6 Marks)
d) The expected number of non-defective bolts in a box is
8
,and the variance is
1.6
.Find the probability that there is only one non-defective bolt in the box.
(3 Marks)
QUESTION TWO
a) The table below shows details of monthly salaries and there corresponding
monthly savings for 10 employees. Use it to answer the following questions.
Employee A B C D E F G H J K
Salary (Ksh ‘000’) 20 35 45 15 20 40 32 52 15 25
Savings (Ksh ‘000’) 6 4 8 7 5 9 7 8 5 8
i. Using the least square method, determine the equation of regression line for salary
on income for the data (10 Marks)
ii. A new employee is to be recruited with a monthly salary set at Ksh 30000. Using
the regression line obtained in (i) above, estimated his expected amount of
savings. (2 Marks)
b) A plant produces steel rods whose weights are known to be normally distributed
with the standard deviation of 2.5kg. A random sample of 40 rods had a mean
weight of 33kg.
i. Find the 99% confidence limits for the population mean. (4 Marks)
ii. Find the probability that a steel rod had weight of 35kg or more (4 Marks)
QUESTION THREE
a) State three assumptions of a binomial distribution. (3 Marks)
b) Explain the meaning of classification of data. (2 Marks)
c) The following distribution gives the difference in age between husband and wife
in a particular community:
Difference
in age
0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80
Frequency 5 18 33 65 76 69 49 35
Determine the:
i. Arithmetic mean correct two decimal places (4 Marks)
ii. Standard deviation. (5 Marks)
iii. Coefficient of dispersion. (3 Marks)
iv. Third quartile (3 Marks)
QUESTION FOUR
a) A department supervisor is considering purchasing a photocopy machine. One
consideration is how often the machine will need repairs. Let
x
denote the
number of repairs during a year. Based on the past performance, the distribution
of
x
is shown as follows.
Number of
repairs ,
x
0 1 2 3
P x 0.2 0.3 0.4 0.1
i. What is the expected number of repairs during a year? (3 Marks)
ii. What is the variance and standard deviation of the number of repairs during a
year? (5 Marks)
b) A committee of
5
people is to be formed randomly from a group of
10
women
and
6
men. Find the probability that the committee has
i.
3
women and
2
men. (3 Marks)
4
ii.
5
women and
1
man. (3 Marks)
iii.
5
women (2 Marks)
iv. At least
3
women. (4 Marks)
QUESTION FIVE
a) Define Spearman’s rank correlation co-efficient. (2 Marks)
b) The table below shows the number of crimes committed in sample communities
during a certain period.
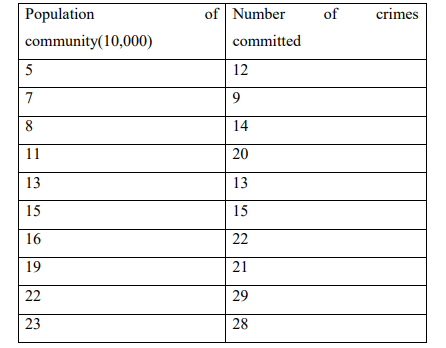
Calculate:
i. a rank correlation for the data
ii. Comment on the value in (i) above.
(10 Marks)
c) Between 2 and 4 pm the average number of phone calls per minute coming in to
the switch board of a company is 2.5. Find the probability that during one
particular minute there will be
i. No phone calls at all. (2 Marks)
ii. Exactly 3 calls. (3 Marks)
iii. At least 2 calls. (3 Marks)
