
UNIVERSITY EXAMINATIONS: 2014/2015
ORDINARY EXAMINATION FOR THE BACHELOR OF SCIENCE
IN INFORMATION TECHNOLOGY
BIT 1301 PROBABILITY AND STATISTICS
DATE: APRIL, 2015 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE (30 Marks)
(a) Define statistics and explain the two broad categories of statistics. (4 marks)
(b) The recovery time after administration of anesthesia to patients undergoing a cardio
vascular surgery is as tabulated below;
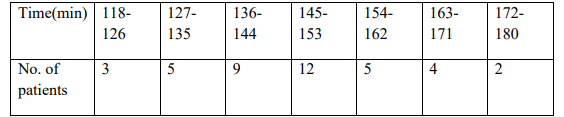
Using the assumed mean method and taking 149 as the assumed mean, calculate the
mean and the standard deviation of the distribution for recovery time. (5marks)
(c) The number of accidents in a production facility has a Poisson distribution with mean
of 2.6 per month.
(i) For a given month what is the probability there will be fewer than two
accidents. (3marks)
(ii) For a given month what is the probability that there will be more than
three accidents. (4marks)
(d) Using appropriate diagrams, briefly explain the following types of distributions:
(i) Platykurtic distribution (2marks)
(ii) Mesokurtic distribution (2marks)
(d) Give a brief distinction between mean absolute deviation and quartile deviation.
Hence obtain the quartile deviation and the mean absolute deviation for the data
below
19,13,14,12,11,1518,14,17,13,19 (7marks)
(f ) The production department of Konza Electronics wants to explore the relationship
between the number of employees who assemble a subassembly and the number
produced. As an experiment, two employees were assigned to assemble the
assemblies. They produced 15 during a one-hour period. Then four employees
assembled them. They produced 25 during a one-hour period. The complete set of
paired observations follows:
Number of Assemblers 1 2 3 4 5
One-Hour production(units) 15 25 10 40 30
Compute the Karl Pearson’s correlation coefficient and comment on the value.
(6marks)
QUESTION TWO (20 Marks)
a) The chair person of Jumuia savings and Sacco would like a measure of association
between their home values and debt based on past experience. The data is given
below;
Home values
85 147 340 94 120 105 135 162 480
Debt data
12 27 45 10 17 4 20 25 35
(i) Compute the spearman rank correlation coefficient and state the relationship
between the variables. (6marks)
(b) A basket contains 7 mangoes and 3 guavas. Three fruits are chosen at random, one at
a time and is not replaced.
(i) What is the probability that all are mangoes (3marks)
(ii) What is the probability that two are mangoes (2marks)
(c) Distinguish between mutually exclusive events and independent events. Let A and B
be two events in a random experiment with P(A)=0.38 and P(B)=0.25.Find the
probability that either A or B occurs if,
(i) A and B are mutually exclusive events.
(ii) A and B are independent events (4marks)
(d) A volunteer ambulance service handles 0 t0 5 calls on a given day. The probability
distribution for the number of calls is as follows.
Number of
service
calls
0 1 2 3 4 5
Probability 0.10 0.15 0.30 0.20 0.15 0.10
(i) What is the expected number of service call? (2marks)
(ii) What is the variance and standard deviation of the number of service calls?
(3 marks)
QUESTION THREE (20 Marks)
(a) Explain the various data types. (4marks)
(b) The following data relates to the heights of employees in a given organization.
Height(cm) Frequency
160-under 165 7
165-under 170 11
170-under 175 17
175-under 180 20
180-under 185 16
185-under 190 9
Calculate
(i) Mean
(ii) Median
(iii) Standard Deviation of the employees in the organization. (9 marks)
(c) The transmission system of a specific car has a warranty of 40,000 miles. It is known
that life of such a transmission system has a normal distribution with a mean of
72,000miles and a standard deviation of 12,000miles.
(i) What percentage of the transmissions will be good for more than
100,000 miles? (3marks)
(ii) What percentage of transmissions will be good between 60,000 and
84,000miles? (4marks)
QUESTION FOUR (20 Marks)
A machine produces the following number of rejects in each successive period of five
minutes
16 21 26 24 11 24 17 25 26 13
27 24 26 3 27 23 24 15 22 22
12 22 29 21 18 22 28 25 7 17
22 28 19 23 23 22 3 19 13 31
23 28 24 9 20 33 30 23 20 8
(a) Construct a frequency distribution from these data using seven class intervals of equal
width
(b) Draw a
(i) frequency histogram and polygon on the same axis
(ii) cumulative frequency curve
(c) Using (b) (i) and (ii) above approximate the mode and the median of the distribution
respectively
(d) Calculate
(i) the mean of the distribution
(ii) the quartile deviation of the distribution (20 marks)
QUESTION FIVE(20Marks)
(a) 5% of all TVS manufactured by a large electronic company are defective; a quality
control inspector randomly selected three TV’s from the production line. What is the
probability that exactly one of these three TV’s is defective? (Use binomial
distribution). (4 marks)
(b) Explain five qualities of a good questionnaire. (5marks)
(d) The height of a child increases at a rate given in the table below. Fit a regression
equation for the data.
Month 1 2 3 4 5 6 7 8 9 10
Height 52.5 58.7 65 70.2 75.4 81.1 87.2 95.5 102.2 108.4
(6 marks)
(d) In a certain statistical distribution, the following results were obtained
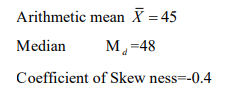
Calculate
(i) Mode
(ii) Standard deviation
