
UNIVERSITY EXAMINATIONS: 2014/2015
ORDINARY EXAMINATION FOR THE BACHELOR OF SCIENCE
IN INFORMATION TECHNOLOGY
BIT 1301 BUSS 202 PROBABILITY AND STATISTICS – DISTANCE
LEARNING
DATE: DECEMBER, 2014 TIME: 2 HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO
QUESTION ONE
a) An urn contains 8 white and 3 red balls. If two balls are drawn at random find the
probability that
i). Both are white
ii). Both are red
iii).One is of each color (6 Marks)
b) A factory has two machines A and B. past records show that machine A produces
40% of the total output and machine B the remaining 60%. Machine A produces 3%
defective articles and machine B produces 1% defective items. An item is drawn at
random and found to be defective. What is the probability that it was produced
i). By machine A
ii). By machine B (8 Marks)
c) The incidence of occupational disease in an industry is such that the workers have a
20% chance of suffering from it. What is the probability that out of six workers, 4 or
more will contact the disease? (8 Marks)
d) In a town 10 accidents take place in a span of 50 days. Assuming that the number of
accidents follows the Poisson distribution, find the probability that there will be 3 or
more accidents in a day. (8 Marks)
QUESTION TWO
a) Construct a frequency table for the following data regarding annual profit, in
thousands of Kenya shillings in 50 firms.
28 35 61 29 36 48 57 67 69 50
48 40 47 42 41 37 51 62 63 33
31 32 35 40 38 37 60 51 54 56
37 46 42 38 61 59 58 44 39 57
38 44 45 45 47 38 44 47 47 64
i). Using 25-34, 35-44, etc., as class intervals, construct a frequency distribution table for the data above (4 marks)
ii). Using the frequency distribution in (i) above, construct a less-than ogive
and find number of firms having profit between ksh. 37,000 and ksh.
58,000. (5 marks)
iii).Calculate the coefficient of variation for this distribution (7 marks)
b) In a moderately skewed distribution, arithmetic mean is 24.6 and the mode is
26.1. Find the value of the median. (4 marks)
QUESTION THREE
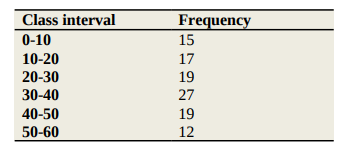
a) Calculate the coefficient of skewness for the following distribution (10 Marks)
b) If A, B, C are mutually exclusive and exhaustive events, find P (B) if
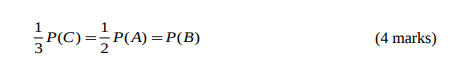
c) A die is thrown at random. What is the expectation of the number on it? (4 Marks)
d) Out of all items sent for refurbishing, 40% had mechanical defects, 50% had electrical defects, and 25% had both. Denoting A = {an item has a mechanical defect} and B
= {an item has an electrical defect}, fill the probabilities into the Venn diagram.
(2 Marks)
QUESTION FOUR
a) Find out the Karl Pearson’s coefficient of correlation between the sales and the expenses of the following 10 firms (figures in ‘000 ksh.). Interpret your results.
(10 Marks)

and probability that B will live
up to 60 years is
What is the probability that
i). Both A and B will live up to 60 years.
ii). Both die before reaching 60 years. (4 Marks)
c) The weekly wages of 1000 workmen are normally distributed around a mean of ksh.
70 with a standard deviation of ksh. 5. Estimate the number of workers whose
weekly wages will be between ksh. 69 and ksh. 72. (6 marks)
QUESTION FIVE
a) The following table gives aptitude test scored and productivity indices of 8 randomly
selected workers. Find the equation to the line which can be used to predict the pro4
ductivity index from the aptitude score. Estimate the productivity index of a worker
whose test score is 66. (12 Marks)

b) The average zinc concentration recovered from a sample of zinc measurements in 36
different locations in the river is found to be 2.6 milligrams per liter. Find the 95%
and 99% confidence intervals for the mean zinc concentration µ . Assume that the
population standard deviation is 0.3. (8 marks)
