
UNIVERSITY EXAMINATIONS: 2021/2022
ORDINARY EXAMINATION FOR BACHELOR OFSCIENCE
INFORMATION TECHNOLOGY, BSc. APPLIED COMPUTING, BSD,
BISF
BIT 1206/ BAC 1201/ BISF 1101/ BSD 1202: DISCRETE
MATHEMATICS
(PARTTIME/ DISTANCE LEARNING)
DATE: DECEMBER, 2021 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One and Any Other Two questions
QUESTION ONE
(a)Use the laws of algebra of sets to simplify
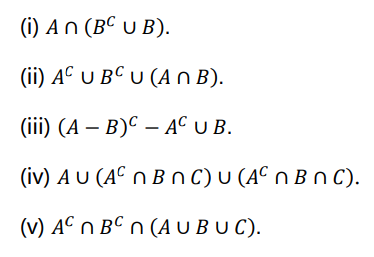
[5Marks]
(b)Prove : if ? is a subset of the null set ? ,then ? = ?.
[5Marks]
(c)Let ? be a subset of ? and let ⅈ: ? ↦ ? be an iclusion
map .Show that the inclusion map is one-to-one.
[5Marks]
(d)Find the largest interval ? on which the formulae
?(?) = ?
2
defines a one to one function.
[5Marks]
QUESTION TWO
(a)Find a traversable trail ? for the graph ? where?(?) =
{?, ?, ?,?} and ?(?) = [{?, ?},{?,?},{?, ?},{?,?},{?,?}] .
[5Marks]
(b)Draw the multigraph ? whose adjacency matrix is
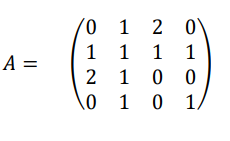
[10Marks]
QUESTION THREE
(a)Determine the number of loops and multiple edges in
a multigraph ? from its adjacency matrix
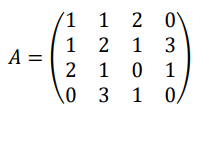
[5Marks]
(b)Let ? be a graph with ? vertices. Describe two major
drawbacks in the computer storage of ? as its adjacency
matrix ?. [10Marks]
QUESTION FOUR
(a)Prove:There is a path from a vertex ? to a vertex ? if and
only if there is a simple path from ? to ?.
[5Marks]
(b)Consider the statement “if Oscar eats Chinese
food,then he drinks milk”.
(i)Write the converse of the statement.
[2Marks]
(ii)Write the contrapositive of the statement.
[2Marks]
(c) Consider the function ?:{1,2,3,4} ↦ {1,2,3,4} given by
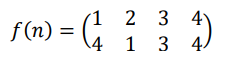
(i) Find ?(1)
[1Mark]
(ii) Find an element ? in the domain such that ?(?) = 1
[1Mark]
(iii) Find an element ? of the domain such that ?(?) = ?
[1Mark]
(iv) Find an element of the condomain that is not in the
range [1Mark]
(d)Consider the function ?: ℤ ↦ ℤ given by ?(?) =
{
? + 1: ? ⋅ ????
? − 3: ? ⋅ ? ⅆⅆ
(i)Is ? injective?Prove your answer
[1Mark]
(ii)Is ? surjective?Prove your answer
[1Mark]