The members of a sample are selected either on a probability basis or by another means. Probability sampling is based on the concept of random selection – a controlled procedure that assures that each population element is given a known nonzero chance of selection.
In contrast, non probability sampling is nonrandom and subjective. Each member does not have a known nonzero chance of being included. Allowing interviewers to choose sample members ‘at random’ (meaning ‘as they wish’ or ‘wherever they find them’) is not random sampling. Only probability samples provide estimates of precision.
Probability Sampling
The unrestricted, simple random sample is the simplest form of probability sampling. Since all probability samples must provide a known nonzero chance of selection for each population element, the simple random sample is considered a special case in which each population element has a known and equal chance of selection. In this section, we use the simple random sample to build a foundation for understanding sampling procedures and choosing probability samples.
1. Simple Random Sampling
In simple random sampling, all study objects have an equal chance of being included in the sample. Researchers begin with a complete list of all members of a population and then choose sample items at random. It should be noted that in simple random sampling, each study object is selected completely independently of other objects. The sampling process involves assigning a unique identification number to each study object in the sampling frame. After this, the researcher must design a method of selecting study objects in
a manner that allows all equal chance of being selected. One way of doing this is writing these identification numbers on small pieces of paper, mixing them thoroughly in a box, and then picking the papers without looking. The numbers on the pieces of paper picked identify the study objects to be included in the sample. In some cases, however, this procedure (lottery method) may be impractical or tedious.
Another procedure used in selecting study objects in simple random sampling involves the use of tables of random numbers. The researcher begins picking randomly objects from any preselected place in the table of random numbers. Then s/he systematically chooses numbers by either moving vertically or horizontally. The sample will therefore consist of the study objects whose numbers are chosen.
Complex probability Sampling
Simple random sampling is often impractical. It requires a population list that is often not available. The design may also be wasteful because it fails to use all the information about a population. In addition, the carrying out of a simple random design may be expensive in time and money. These problems have led to the development of alternative designs that are superior to the simple random design in statistical and/or economic efficiency.
A more efficient sample in a statistical sense is one that provides a given precision (standard error of the mean) with a smaller sample size. A sample that is economically more efficient is one that provides a desired precision at a lower dollar cost. We achieve this with designs that enable us to lower the costs of data collecting, usually through reduced travel expense and interviewer time.
In the discussion that follows, four alternative probability sampling approaches are considered: systematic, stratified, cluster and multi-stage.
2. Systematic Sampling
This method is frequently used in production and quality control sampling. In this approach, every n’th element in the population is sampled, beginning with a random start of an element in the range of 1 to n. After a randomly selected start point(s) a sample item would be selected every n’th item. Assume that in an assembly line it was decided to sample every 100th item and a start point of 67 was chosen randomly, the sample would be the following items: 67th; 167th; 267th; 367th; and so on The gap between selections is known as the sampling interval and is itself often randomly selected. A concern with this technique is the possible periodicity in the population that may coincide with the sampling interval and cause bias.
3. Stratified Sampling
Most populations can be segregated into several mutually exclusive sub-populations, or strata. Thus, the process by which the sample is constrained to include elements from each of the segments is called stratified random sampling.
There are three reasons why a researcher chooses a stratified sample:
• To increase a sample’s statistical efficiency;
• To provide adequate data for analysing the various subpopulations, and
• To enable different research methods and procedures to be used in different strata.
With the ideal stratification, each stratum is homogeneous internally and heterogeneous with other strata.
The size of the strata samples is calculated with two pieces of information:
- How large the total sample should be and
- How the total sample should be allocated among strata.
Proportional versus Disproportionate Sampling
In proportionate stratified sampling the number of items drawn from each stratum is equal. Suppose a researcher needs a sample from a universe of 500 individuals, ie, n = 500. If she were to select 4 strata ie, s1, s2, s3, and s4, each would have 125 items. A simple random sample is then selected independently from each group. In disproportionate sampling, no equal units are drawn but weights are assigned to each stratum. Suppose again the researcher has a sample of 500 which represent income level groups, ie:
Income (Ksh) below 5,000 s1 = 0.4 (500) = 200.
Income (Ksh) 5,000 – 10,000 = s1 = 0.3 (500) = 150
Income (Ksh) 10,000-50,000 = s3 = 0.2 (500) = 100
Income (Ksh) above 50,000 = s4 = 0.1 (500) = 50
Random samples are taken from within each group in the proportions that each group bears to the population as a whole. The purpose of stratification is to ensure that the sample mirrors the characteristics of the population. In the case of the study of incomes, by assigning a higher weight to low income groups, the researcher is likely to get a good sample representative. The main difference between stratified random sampling and simple random sampling is that in the simple random method, sample items are chosen at random from the entire universe, while in the stratified random sampling, the sample items are chosen at random from each stratum.
4. Cluster Sampling
In a simple random sample, each population element is selected individually. The population can also be divided into groups of elements with some groups randomly selected for study. This is cluster sampling. An immediate question might be: How does this differ from stratified sampling? They may be compared as follows:

When done properly, cluster sampling also provides an unbiased estimate of population parameters. Two conditions foster the use of cluster sampling: (1) the need of more economic efficiency than can be provided by simple random sampling and (2) the frequent unavailability of a practical sampling frame for individual elements. Statistical efficiency for cluster samples is usually lower than for simple random samples chiefly because clusters are usually homogeneous. Families in the same block (a typical cluster) are often similar in social class, income level, ethnic origjn, and so forth.
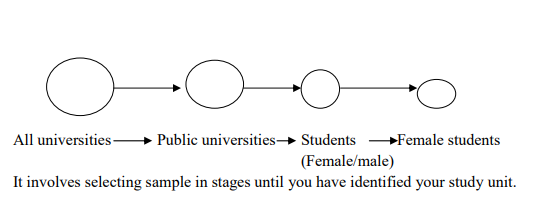
4. Multi-Stage Sampling
This is a practical system widely used to reduce the travelling time for interviewers and the subsequent costs multi-stage sampling is similar to stratified sampling except the groups and sub-groups are selected on a geographical / location basis rather than some social characteristics. For example: Assume you wanted the opinion of female students from universities on gender equality. You would select your sample as:
Non-Probability Sampling
Any discussion of the relative merits of probability versus non probability sampling clearly shows the technical superiority of the former. In probability sampling, researchers use a random selection of elements to reduce or eliminate sampling bias. Under such conditions, we can have substantial confidence that the sample is representative of the population from which it is drawn. In addition, with probability sample designs, we can estimate an interval range within which the population parameter is expected to fall. Thus, we not only can reduce the chance for sampling error but also can estimate the range of probable sampling error present.
With a subjective approach like non probability sampling, the probability of selecting population elements is unknown. There are a variety of ways to choose persons or cases to include in the sample. Often we allow the choice of subjects to be made by field workers on the scene. When this occurs, there is greater opportunity for bias to enter the sample selection procedure and to distort the findings of the study. Also, we cannot estimate any range within which to expect the population parameter. Given the technical advantages of probability sampling over non probability sampling, why would anyone choose the latter? There are some practical reasons for
using these less precise methods.
Practical Considerations
We may use non probability sampling procedures because they satisfactorily meet the sampling objectives. While a random sample will give us a true cross section of the population, this may not be the objective of the research. If there is no desire or need to generalize to a population parameter, then there is much less concern about whether the sample fully reflects the population. Often researchers have more limited objectives. They may be looking only for the range of conditions or for examples of dramatic variations. This is especially true in exploratory research where one may wish to contact only certain persons or cases that are clearly typical.
Additional reasons for choosing non probability over probability sampling are cost and time.
Probability sampling clearly calls for more planning and repeated callbacks to ensure that each selected sample member is contacted. These activities are expensive. Carefully controlled non probability sampling often seems to give acceptable results, so the investigator may not even consider probability sampling. While probability sampling may be superior in theory, there are breakdowns in its application. Even carefully stated random sampling procedures may be subject to careless application by the people involved. Thus, the ideal probability sampling may be only partially achieved because of the human element.
It is also possible that non probability sampling may be the only feasible alternative. The total population may not be available for study in certain cases. At the scene of a major event, it may be infeasible to even attempt to construct a probability sample. A study of past correspondence between two companies must use an arbitrary sample because the full correspondence is normally not available.
In another sense, those who are included in a sample may select themselves. In mail surveys, those who respond may not represent a true cross section of those who receive the questionnaire. The receivers of the questionnaire decide for themselves whether they will participate. There is some of this self-selection in almost all surveys because every respondent chooses whether to be interviewed.
Methods
1. Convenience. Non probability samples that are unrestricted are called convenience samples. They are the least reliable design but normally the cheapest and easiest to conduct. Researchers or field workers have the freedom to choose whomever they find, thus the name convenience. Examples include informal pools of friends and neighbors or people responding to a newspaper’s invitation for readers to state their positions on some public issue.
While a convenience sample has no controls to ensure precision, it may still be a useful procedure. Often you will take such a sample to test ideas or even to gain ideas about a subject of interest. In the early stages of exploratory research, when you are seeking
guidance, you might use this approach. The results may present evidence that is so overwhelming that a more sophisticated sampling procedure is unnecessary. In an interview with students concerning some issue of campus concern, you might talk to 25 students
selected sequentially. You might discover that the responses are so overwhelmingly onesided that there is no incentive to interview further.
2. Purposive Sampling. A non probability sample conforms to certain criteria is called purposive sampling. There are two major types – judgement sampling and quota sampling.
- Judgement Sampling occurs when a researcher selects sample members to conform to some criterion. In a study of labor problems, you may want to talk only with those who have experienced on-the-job discrimination. Another example of judgement sampling occurs when election results are predicted from only a few selected precincts that have been chosen because of their predictive record in past elections. When used in the early stages of an exploratory study, a judgement sample is appropriate.
When one wishes to select a biased group for screening purposes, this sampling method is also a good choice. Companies often try out new product ideas on their employees. The rationale is that one would expect the firm’s employees to be more favorably disposed toward a new product idea than the public. If the product does not pass this group, it does not have prospects for success in the general market. - Quota Sampling is the second type of purposive sampling. We use it to improve representativeness. The logic behind quota sampling is that certain relevant characteristics describe the dimensions of the population. If a sample has the same
distribution on these characteristics, then it is likely representative of the population regarding other variables on which we have no control. Suppose the student body of Mount Kenya is 55 percent female and 45 percent male. The sampling quota would call
for sampling students at a 55 to 45 percent ratio. This would eliminate distortions due to a non representative gender ratio.
In most quota samples, researchers specify more than one control dimension. Each should meet two tests: (1) it should have a distribution in the population that we can estimate. (2) It should be pertinent to the topic studied. We may believe that responses to a question should vary, depending on the gender of the respondent. If so, we should seek proportional responses from both men and women. We may also feel that undergraduates differ from graduate students, so this would be a dimension. Other dimensions such as the student’s academic discipline, ethnic group, religious affiliation, and social group affiliation may be
chosen. Only a few of these controls can be used. To illustrate, suppose we consider the following:
Gender – two categories – male, female
Class level – two categories – graduate and undergraduate
College – six categories – Arts and Science, Agriculture, Architecture, Business,
Engineering, other
Religion – four categories – Protestant, Catholic, Jewish, other
Fraternal affiliation – two categories – member, nonmember
Family social-economic class – three categories – upper, middle, lowerQuota sampling has several weaknesses. First, the idea that quotas on some variables assume representativeness on others is argument by analogy. It gives no assurance that the sample is representative on the variables being studied. Often, the data used to provide controls may also be dated or inaccurate. There is also a practical limit on the number of simultaneous controls that can be applied to ensure precision. Finally, the choice of subjects is left to field workers to make on a judgemental basis. They may choose only friendly looking people, people who are convenient to them, and so forth. Despite the problems with quota sampling, it is widely used by opinion pollsters and marketing and other researchers. Probability sampling is usually much more costly and time consuming. Advocates of quota sampling argue that while there is some danger of systematic bias, the risks are usually not that great. Where predictive validity has been checked (e.g., in election polls), quota sampling has been generally satisfactory.
3. Snowball. This design has found a niche in recent years in applications where respondents are difficult to identify and are best located through referral networks. In the initial stage of snowball sampling, individuals are discovered and may or may not be selected through probability methods. This group is then used to locate others who possess similar characteristics and who, in turn, identify others. Similar to a reverse search for bibliographic sources, the ‘snowball’ gathers a subject as it rolls along. Variations on snowball sampling have been used to study drug cultures, teenage gang activities, power elites, community relations, insider trading and other applications where respondents are difficult to identify and contact.
4. Dimensional Sampling. The researcher identifies the various characteristics of interest in a population and obtains at least one correspondent for every combination of those factors. It is a further refinement of the quota sampling technique. (ie, you have a number of features, male/female, so you choose one man to represent the men and one woman to represent the women).
