FRIDAY: 3 September 2021. Time Allowed: 3 hours.
Answer ALL questions. Marks allocated to each question are shown at the end of the question. Show ALL your workings.
QUESTION ONE
1. The Aviation Perspectives Agency (APA) recently conducted a market survey to determine the air travel preferences of 170 travellers in a certain country. The air travel preferences were represented by the following airlines; Excellent Airways, Safari Connections and Tumaini Services.
The following results were obtained from the survey:
100 travellers preferred Excellent Airways.
40 travellers preferred Safari Connections.
75 travellers preferred Tumaini Services.
20 travellers preferred Excellent Airways and Safari Connections.
28 travellers preferred Excellent Airways and Tumaini Services.
18 travellers preferred Safari Connections and Tumaini Services.
9 travellers did not record any preference.
Required:
Represent the above information in a Venn diagram. (4 marks)
Determine the number of travellers who preferred all the three airlines. (3 marks)
The number of travellers who preferred the Safari Connections and Tumaini Services, but not the Excellent Airways. (1 mark)
2. The following data presents the quarterly imports of electrical products by a certain electronics company for the given four-year period:
Imports in Sh.”Million”
Year
Quarter 1 Quarter 2 Quarter 3 Quarter 4
2017 43 71 83 59
2018 50 82 93 75
2019 62 89 101 81
2020 73 95 120 89
Required:
Using 4-quarter moving averages, calculate the seasonal variations from the above data. (8 marks)
Derive the deseasonalised data for the imports using the additive model. (4 marks)
(Total: 20 marks)
QUESTION TWO
1. Explain any four assumptions underlying the game theory. (4 marks)
2. Zakem Ltd. produces two products namely; “Alkon” and “Zenon”. The products pass through three departments
namely; Assembly, Finishing and Packaging. There is a maximum of 200 hours in each of the Assembly and Finishing departments.
In addition, a maximum of 400 hours of packaging are available for packing “Alkon” and “Zenon”.
The table below shows the number of hours required per unit of each product:

Each unit of “Alkon” and “Zenon” gives a profit contribution of Sh.3,000 and Sh.2,000 respectively.
Required:
Formulate a linear programming model to solve the above problem. (2 marks)
Using the simplex method, solve the linear programming model formulated in above. (14 marks)
(Total: 20 marks)
QUESTION THREE
1. The demand function for a certain product is given by:
P = 0.3Q — 5 Where:
P is the price in shillings of the product per unit; and Q is the quantity of the product demanded in units.
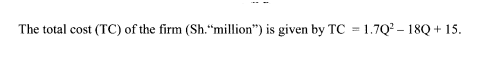
Required:
The break-even point quantity (in units). (2 marks)
The level of output (in units) that maximises profit. (4 marks)
2. Explain the difference between “point estimate” and “confidence interval”. (4 marks)
Mali Mali Supermarkets (MMS) operates two branches, one in Kisumu and the other in Mombasa. The management has received complaints that there is a significant difference between the wages paid to employees in the two branches.
A sample of 40 employees was taken from the Kisumu branch and it had a mean wage of Sh.12,000 and a standard deviation of Sh.1,000. A sample of 50 employees taken from the Mombasa branch had a mean wage of Sh.13,000 and a standard deviation of Sh.1,200.
Required:
Advise the management of MMS on whether there is a significant difference between the wages paid in Kisumu branch and Mombasa branch.
(Use a significance level of 5%). (10 marks)
(Total: 20 marks)
QUESTION FOUR
1. Explain the difference between “correlation coefficient” and “coefficient of determination” as used in regression
analysis. (4 marks)
2. A group of eight students were tested in “Quantitative Analysis” and “Auditing” examinations. The marks scored were as follows:
Marks in percentage (%)
Student Quantitative Analysis Auditing
A 76 82
B 43 57
C 49 75
D 84 86
E 69 68
F 69 92
G 53 43
H 36 53
Required:
Compute the Spearman’s rank correlation coefficient and interpret the results. (8 marks)
3. A medium-sized company manufactures product “Ndovu”. The current variable production cost per unit of product “Ndovu” is Sh.800 while the selling price is Sh.1,150 per unit. However, the demand for product “Ndovu” is uncertain and has the following probability distribution:
Number of units of Probability
product “Ndovu” demanded
10 0.36
20 0.42
30 0.22
Required:
Advise the company on the optimal number of units of product “Ndovu” to produce using the:
Expected monetary value (EMV) criterion. (4 marks)
Hurwicz criterion. Assume a coefficient of optimism of 0.8. (4 marks)
(Total: 20 marks)
QUESTION FIVE
1. Summarise four practical limitations of the “queuing model”. (4 marks)
2. A recent inspection of bolts produced by a certain company revealed that 16 bolts were defective out of a total of 40 bolts inspected.
5 bolts are picked at random and inspected.
Required:
Assuming that the distribution of defective bolts follows the poisson distribution, calculate the probability that at least three bolts are defective. (4 marks)
Assuming that the distribution of defective bolts follows the binomial distribution, calculate the probability that at most 3 bolts are defective. (4 marks)
3. ABC Limited is a construction company. An engineer identified the following activities to complete a project and their estimated expected time in weeks.
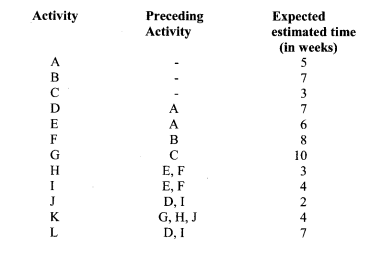
Required:
Draw a network diagram to represent the above project. (6 marks)
Obtain the critical path and project duration. (2 marks)
(Total: 20 marks)
