WEDNESDAY: 3 August 2022. Morning paper. Time Allowed: 3 hours.
Answer any FIVE questions. ALL questions carry equal marks. Show ALL your workings. Do NOT write anything
on this paper.
QUESTION ONE
1. Soundex Company has received an order to supply 900 tables, 1,200 desks and 2,000 chairs. The management of Soundex Company has decided that 500 tables, 800 desks and 1,300 chairs could be supplied from their city centre branch and the balance of the order could be filled from their industrial area branch. Production of each table requires 3 hours in the machining department, 5 hours in the assembly department and 4 hours in the finishing department. Production of a desk requires 4 hours in the machining department, 8 hours in the assembly department and 6 hours in the finishing department. Production of a chair requires 2 hours in the machining department, 3 hours in the assembly department and 5 hours in the finishing department.
The cost of an hour in the machining, assembly and finishing department is Sh.50, Sh.100 and Sh.150 respectively.
Required:
Using matrix algebra:
Calculate the total number of hours required at each branch. (6 marks)
Calculate the total cost incurred at each branch and the total cost incurred by Soundex Company to supply the order. (4 marks)
2. The data below relates to the sales of Madi and Sons Electrical Company for the six months ending 30 June 2022:
Month January February March April May June
Sales (Sh.“000”) 80 76 78 82 72 82
Required:
Using exponential smoothing with a smoothing constant (α) of 0.25, determine the forecast sales for the month of July 2022. (4 marks)
3. The number of employees working online during a particular week was recorded as shown below:
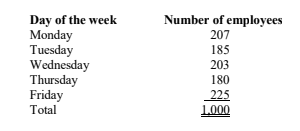
Required:
Test the hypothesis that the number of employees who worked online does not depend on the day of week. Use a significance level of 1%. (6 marks)
(Total: 20 marks)
QUESTION TWO
1. TMA Company produces three products; Standard, Deluxe and Luxury in three of its departments which are Cutting, Assembly and Finishing. The total available labour hours per week for Cutting, Assembly and Finishing departments are 180, 300 and 240 respectively. To produce two units of Standard requires 240 minutes in the Cutting department, half the amount of time in the
Assembly department and same amount of time in the Finishing department as in the Cutting department. To produce one unit of Deluxe requires 60 minutes, 180 minutes and 60 minutes in Cutting, Assembly and Finishing departments respectively.
To produce three units of Luxury requires 180 minutes in Cutting department and twice the amount of time in both Assembly and Finishing departments. The contribution per unit from Standard, Deluxe and Luxury is Sh.6, Sh.5 and Sh.2 per unit respectively.
Required:
Formulate the above problem as a linear programming model. (6 marks)
Prepare an initial simplex tableau to solve the above model. (4 marks)
2. The above problem was solved using a statistical software and the final simplex tableau is provided below:
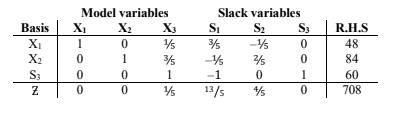
Required:
1. Explain whether the solution is optimal. Justify your answer. (2 marks)
2. Determine the optimal solution for TMA Company. (2 marks)
3. Determine the slack or surplus value for each constraint. State which one is a slack and which one is a surplus. (4 marks)
4. Determine the shadow price for each constraint. (2 marks)
(Total: 20 marks)
QUESTION THREE
1. Explain the term “Markov analysis”. (2 marks)
Highlight four assumptions of Markov analysis. (4 marks)
2. Differentiate between the following sets of terms as used in hypothesis testing:
“Null hypothesis” and “alternative hypothesis”. (2 marks)
“Parameter” and “statistic”. (2 marks)
3. The following payoff matrix shows the potential profits in millions of shillings which are expected to arise from launching four products S1, S2, S3 and S4 for each level of demand; low, moderate or high.
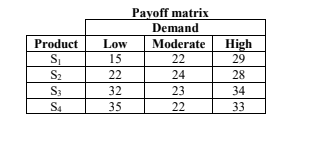
Required:
Assuming that the products are mutually exclusive, evaluate the optimal decision using:
Maximax criterion. (3 marks)
Maximin criterion. (3 marks)
Minimax regret criterion. (4 marks)
(Total: 20 marks)
QUESTION FOUR
1. A proposal to teach longer hours on weekdays rather than have weekend classes was put forward by a subject lecturer to his students.
The following results were obtained:
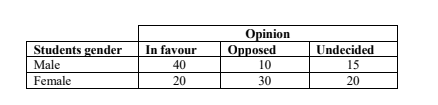
Required:
Calculate the probability that a student selected at random will be:
Female and in favour of the proposal. (2 marks)
Either male or opposed to the proposal. (2 marks)
Undecided given that the student is female. (2 marks)
2. The Production Manager of AMIK Company has provided the following information relating to the number of units produced per day in the last 172 days:

Required:
The modal production. (2 marks)
The median production. (2 marks)
The quartile deviation of the production. (6 marks)
3. A curve is defined by the quadratic function
![]()
Required:
Determine the roots of the equation using the factorisation method. (2 marks)
By using differentiation, determine the coordinates of the turning point of the curve. (2 marks)
(Total: 20 marks)
QUESTION FIVE
1. ABC Ltd. has introduced a new product branded “Nilan”. The Production Manager wishes to establish the relationship between the total cost of production and the number of units produced. The Production Manager also believes that the relationship between the total cost of producing “Nilan” and the number of units produced is linear in nature.
The Production Manager has gathered the following data on the production for the last 8 months:
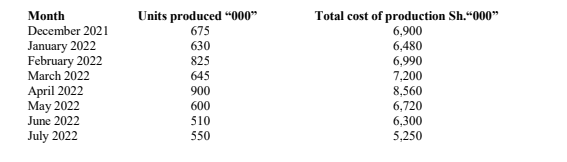
Required:
Estimate the total cost function using the ordinary least squares method. (7 marks)
The coefficient of determination between the number of units produced and the total cost of production. (2 marks)
Interpret your answer in 1 (ii) above. (1 mark)
2. A survey of 850 residents of a certain town aimed at finding out the brand of vehicles owned, produced the following results:
316 residents owned Nissan vehicles.
160 residents owned Honda vehicles.
360 residents owned Toyota vehicles.
120 residents owned both Nissan and Toyota vehicles.
56 residents owned both Nissan and Honda vehicles.
80 residents owned both Honda and Toyota vehicles.
240 residents did not own any of the three brands of vehicles.
Required:
Present the above information in the form of a Venn diagram. (5 marks)
The number of residents who own all the three brands of vehicles. (3 marks)
The number of residents who own just one of the three brands of vehicles. (2 marks)
(Total: 20 marks)
QUESTION SIX
1. Outline four qualities of a good average. (4 marks)
2. The weights of 1,000 items are normally distributed with a mean weight of 200 kgs and a standard deviation of 22 kgs.
Required:
Determine the number of items that have weights between 210 kgs and 220 kgs. (2 marks)
Determine the number of items that have weights between 180 kgs and 230 kgs. (2 marks)
Calculate the weight below which 20% of the items fall. (2 marks)
3. The data below shows the probability distribution of profits earned by firms in the manufacturing industry:
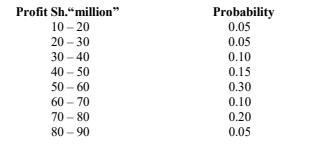
Required:
The expected profit. (4 marks)
The expected standard deviation. (4 marks)
The coefficient of variation. (2 marks)
(Total: 20 marks)
QUESTION SEVEN
1. A technician at Light Industries Ltd. has established that the probability of a production process producing defective output is 0.2. A total of 60 units are produced from the process in a certain production period.
Required:
The probability that exactly 10 of the units will be defective assuming a poisson distribution. (3 marks)
The probability that exactly 10 of the units will be defective assuming a binomial distribution. (2 marks)
The expected number and standard deviation of units expected to be defective assuming a binomial distribution. (2 marks)
2. XYZ Ltd. produces and sells a product branded “Xedo”. The product is produced in two departments; manufacturing and assembly.
The marginal revenue (MR) of XYZ Ltd. is given by the function
MR = 600 – 0.12q
Where q is the number of units produced and sold.
The total variable cost (VC) for the two departments is given as follows:

Required:
The total revenue, total cost and profit functions of XYZ Ltd. (6 marks)
The profit maximising level of output. (2 marks)
The maximum profit of XYZ Ltd. (1 mark)

