 UNIVERSITY EXAMINATIONS: 2015/2016
UNIVERSITY EXAMINATIONS: 2015/2016
EXAMINATION FOR THE CERTIFICATE IN BRIDGING
MATHEMATICS
MAT104 STATISTICS & PROBABILITY
DATE: AUGUST 2016 TIME: 1½HOURS
INSTRUCTIONS: Answer Any THREE Questions.
QUESTION ONE
a) Define the terms
i) Statistics (2 Marks)
ii) Probability distribution (2 Marks)
b) Consider the following data:
X 2 4 6 7 8 10
f 3 4 5 3 2 2
Compute:
i) The mean (3 Marks)
ii) The inter-quartile range (5 Marks)
iii) The 6th decile (3 Marks)
c) A bag contains 5 ripe mangoes and 6 unripe ones. John picks two mangoes at random one
after the other and gives it to his sister Esther only if it is ripe and if not returns it back into the
basket. Using a probability tree diagram, compute the probability that Esther gets at least one
ripe fruit.
2
(5 Marks)
d) The following frequency table gives the height in metres of some trees in a plantation:
class 1.5-
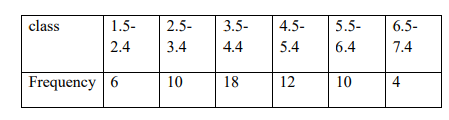
Frequency 6 10 18 12 10 4
i) Represent this information in cumulative frequency (ogive) curve (5 Marks)
ii) From the ogive curve estimate the boundary height if the trees are classified as 20% retarded,
50% standard and the rest overgrown
(3 Marks)
c) By calculation, find the position of a tree with a height of 5.7 metres (2 Marks)
QUESTION TWO
Consider the following data:
0 – 9,999
10,000 – 19,999
20,000 – 29,999
30,000 – 39,999
40,000 – 49,000
50,000 – 59,000
60,000 – 69,000
70,000 – 79,000
80,000 – 89,000
90,000 – 99,999
Required:
i) Compute the mean using 64,500 as an assumed mean (5 Marks)
3
ii) Compute the variance and standard deviation using 64,500 as an assumed mean(8 Marks)
iii) Compute the inter-quartile range (7 Marks)
QUESTION THREE
a) The price of a commodity increased by 35% between 2010 and 2014 but declined by 24%
between 2014 and 2015. Using the price relative concepts determine the percentage change in
the price of the commodity between 2010 and 2015.
(4 Marks)
b) The following table shows the monthly cost of living in two estates, estate A and B in Nairobi
in year 2015 and the significance/weight of each commodity:
Item Town A Cost (Shs) Town B Cost (Shs) Weight

Nancy is trying to establish where to reside at the lowest cost possible. Taking Town A as the
base town compute the composite/cost of living index and advise her accordingly.
(10 Marks)
c) A sample containing 10 values has a mean of 5 and a standard deviation of 3. Without
compotation explain what the standard deviation and the mean shall be if all the values are
multiplied by 3.
(2 Marks)
d) A discrete random variable X takes the following values with the corresponding probabilities:
x -30 -10 0 10 20 30
P(x) 0.1 K 0.15 K 0.1 0.25
Find:
i) The value of k (1 Mark)
ii) P(x˃0) (1 Mark)
iii) Mean of x (2 Marks)
QUESTION FOUR
a) Describe the following terms:
i) Probability (2 Marks)
ii) Mutually exclusive events (2 Marks)
iii) Set (2 Marks)
b) A fair six sided dice is painted Yellow on two of its faces and red on the remaining faces. A
game is played such that you win Ksh 50 if you get a yellow face and lose Ksh 30, if you get a
red dice. The dice is tossed five times. Let X represent the event yellow occurs:
i) Provide the probability distribution function of X and hence how much one would expect to
earn in this game
(12 Marks)
(II) The probability that one earns Ksh 200 (2 Marks)
QUESTION FIVE
The following data relates to the number of absent students at a school on monthly basis for 12
months of the year:

i) Compute the four point moving averages and centre them (8 Marks)
ii) Plot the time series data on a graph (5 Marks)
iii) Super-impose the line of best fit on the time series graph (5 Marks)
iv) Comment on the general trend of the data (2 Marks)
