
UNIVERSITY EXAMINATIONS: 2016/2017
EXAMINATION FOR THE CERTIFICATE IN BRIDGING
MATHEMATICS
MAT102 GEOMETRY
DATE: DECEMBER, 2016 TIME: 1 ½ HOURS
INSTRUCTIONS: Answer Question ONE and any TWO questions.
QUESTION ONE
a) A surveyor sets up a theodolite some distance from a pylon and finds that the angle of
elevation to the top of the pylon to be 25°. He then moves 50 metres nearer and observes that the
angle of elevation to be 50ᶿ. Find the height of the pylon assuming the instrument has a height of
1.8 metres.
(6 Marks)
b) Solve triangle ABC using the cosine rule: a= 12cm, b= 9cm and angle C= 118°.
(6 Marks)
c) Calculate the interior angles of a regular polygon with 12 sides. (4 Marks)
d) Two of the exterior angles of a polygon are 63° each while the remaining are each 26°. How
many sides does the polygon have? (4 Marks)
e) Find the diameter of a circumscribing circle of triangle ABC such that A= 75°, B= 48° and a=
21 cm.
(4 Marks)
f) A ship which can travel at 10 knots is at a point with the latitude 40°S, longitude 30°W. Find
the time taken for the ship to reach the equator.
(6 Marks)
QUESTION TWO
a) Solve triangle ABC using sine rule given A= 61°, B= 71° and b= 91 mm
(6 Marks)
b) A ship sends a radio message saying it is in distress and giving its position as (50°N, 20°W).
The signal is picked up by a ship A at (50°N, 15°W) and a ship B at (53°N, 20°W). Both ships
can move at the speed of 20 knots
i) Calculate the length of time each ship will take to the distressed ship, assuming A sails due
west and B sails due south.
(6 Marks)
ii) If the distressed ship is drifting due east at 4 knots, find the new position it should radio 5
hours later
(4 Marks)
c) The longitude of Moshi in Tanzania and Lucknow in India are 38°E and 81°E respectively.
What will be the time in Lucknow when it is noon in Moshi.
(4 Marks)
QUESTION THREE
a ) Prove the identities:
i) Cos2 X- Sin2 X = 1 – 2Sin2 X (5 Marks)
ii) Cos2 X – Sin2 X = 2Cos2 X – 1 (5 Marks)
b) a2= b2+ c2
– 2bc Cos A. Using a suitable explanations and diagram prove it (10 Marks)
QUESTION FOUR
a) The angles of a quadrilateral are x, 5x, 4x and 2x. Find the value of these angles.
(6 Marks)
b) Explain THREE characteristics that can prove that two triangles are congruent. (6 Marks)
c) Generate the trigonometric ratios of special angles 30° and 60° without calculator computation
(hint: use a triangle)
(8 Marks)
QUESTION FIVE
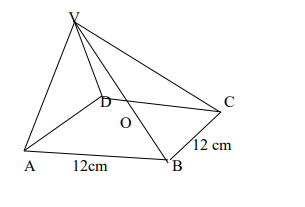
The figure above shows a pyramid VABCD with a square base of 10cm and each of its slanting
edge 15 cm long. O is the centre of the base. Calculate:
i) The length of OB (5 Marks)
ii) The height VO (5 Marks)
iii) The angle between VB and the base (5 Marks)
iv) The angle between the plane VAB and the base (5 Marks)
