UNIVERSITY EXAMINATIONS: 2015/2016
EXAMINATION FOR THE CERTIFICATE IN BRIDGING
MATHEMATICS
MAT102 GEOMETRY
DATE: AUGUST 2016 TIME: 1½HOURS
INSTRUCTIONS: Answer Any THREE Questions.
QUESTION ONE
a) The angles of a quadrilateral are x, 5x, 4x and 2x. Find the value of these angles (4 Marks)
b) Explain THREE characteristics that can prove that two triangles are congruent (3 Marks)
c) Find the distance between Monrovia (6.3° N; 10.8° W) and Benin City (6.3° N; 5.7° E) in
Kms and Nautical miles (4 Marks)
d) An Aeroplane flies from a point P (21 N, 32 E) southwards at 850km/hr. Find its position Q
after 4 hrs. (3 Marks)
e) Find the time difference between two places whose coordinates are:
– M (112° E 14° N) and N (49° W, 18° S) (2 Marks)
– P (15° W; 30° S) and Q(24° W 12° S) (2 Marks)
f) To find the height of a tower a surveyor stands some distance away from the base of the tower
and observes the angle of elevation to the top of the tower to be 45°. He then moves 80m nearer
and observes that the angle of elevation to be 60°. Find the height of the tower. (5 Marks)
g) Solve the triangle ABC using the sine rule given a= 23 cm, c= 18.2 cm and A= 49.32°
(5 Marks)
2
h) Find the diameter of a circumscribed circle of the triangle ABC given:
C= 100°, B = 50° and b= 90mm (2 Marks)
QUESTION TWO
a) The cosine rule states that
. Using a suitable explanations and diagram prove it (10 Marks)
b) Hence use the cosine rule to solve triangle ABC where a= 9 cm, b=11 cm and C= 60°
(5 Marks)
c) Generate the trigonometric ratios of special angles 30° and 60° without calculator computation
(hint: use a right angled triangle)
(5 Marks)
QUESTION THREE
a) A plane passes over a point P (20°E, 26°N) and flies due south for 8 hrs at a rate of 540 knots
until it is over a point Q ( 20°E, α° S). The plane then flies to a point R for 1 hr at the same
speed. Calculate to the nearest degree:
i) The value of α (5 Marks)
ii) The longitude of R (5 Marks)
b) A man standing on top of a cliff 100m high observes that the angles of depression of two
object on the ground to be 18° and 22°. Calculate the distance between the two objects
(5 Marks)
QUESTION FOUR
a) Construct triangle ABC where, A= 75°, B= 34° and a= 10 cm (5 Marks)
b) Construct an inscribed circle with center O (5 Marks)
c) Measure the size of the radius of the circle (2 Marks)
d) Calculate the size of interior angles of a regular polygon with 15 sides (3 Marks)
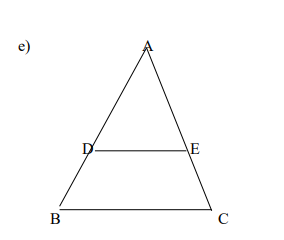
In triangle ABC, DE is // to BC. If AD= 3 cm, DB= 4cm and DE= 6cm. Find the length of BC.
(3 Marks)
f) Triangles ABC and XYZ are known to be similar with heights equal to 20cm and 60 cm
respectively. If the area of triangle ABC is 80cm2, find the area of triangle XYZ .
(2 Marks)
QUESTION FIVE
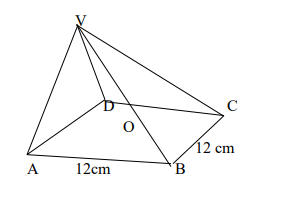
The figure above shows a pyramid VABCD with a square base of 12cm and each of its slanting
edge 15 cm long. O is the center of the base. Calculate:
i) The length of OB (4 Marks)
ii) The height VO (4 Marks)
iii) The angle between VB and the base (4 Marks)
iv) The angle between the plane VAB and the base (4 Marks)
b) Provide TWO characteristics that prove that two triangles are similar (4 Marks)
