
UNIVERSITY EXAMINATIONS: 2016/2017
EXAMINATION FOR THE CERTIFICATE IN BRIDGING
MATHEMATICS
MAT101 ALBEBRA & BUSINESS MATHEMATICS
DATE: AUGUST, 2017 TIME: 2 HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions.
QUESTION ONE
a) Solve the following equations by factors method


QUESTION TWO
a) Express each of their following in the simplest forms possible:

f) A certain sum of money, at compound interest, amounts to shs 5,250 at the end of
the first year and to 5512.5 at the end of the second year. Find
i. The interest rate percent and (4 Marks)
ii. The principal amount. (4 Marks)
QUESTION THREE
a) When a body moves with uniform speed, the distance (d) moved varies directly as the
time (t) taken
i. express the relation between d and t (4 Marks)
ii. When d = 25m, t = 1.25s. Find the law connecting d and t (4 Marks)
iii. Find t when d = 90m (4 Marks)
b) Find the values of x and y if
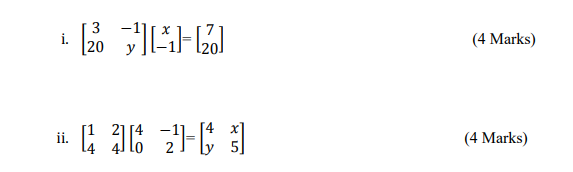
QUESTION FOUR
a) It is estimated that the population of a town increases by 4% each year. If the
population of the town was 425,000 on 1st January 2016, find what it would be (to the
nearest thousand) on the 31st December 2017 (5 Marks)
c) The value of K £ 15,000 of a house rose by 25% in the first year, by 10% the second
year but dropped by 20% in the third year. Find its value after the three years(5Marks)
d) A scientific calculator marked at shs 1560 under hire purchase. It is available for a
down payment (deposit) of shs 200 and six monthly installments of shs 250 each.
Calculate
i. The hire purchase price (5 Marks)
ii. The extra amount paid over cash price. (5 Marks)
QUESTION FIVE
a) The fourth term of an arithmetic progression is 79 and its 11th term is 100. Find the
first term, the common difference and the 21st term (4 Marks)
b) Solve for x given
