
UNIVERSITY EXAMINATIONS: 2017/2018
EXAMINATION FOR THE CERTIFICATE IN BRIDGING
MATHEMATICS
MAT 102: GEOMETRY
DATE: DECEMBER, 2017 TIME: 1 ½ HOURS
INSTRUCTIONS: Answer Question ONE and any other TWO questions.
QUESTION ONE
a) Two places on the equator lie on longitude 63° and 132 ° . How far apart are they measured along
the equator in KMs an nm?
(5 Marks)
b) Two planes A and B took off at JKIA (1°S, 37°E) at 11 pm on Monday. Plane A flew due east while B
flew due west. If they met after again after 18 hours at (1°S, 117°W), calculate:
i) Their respective speeds (7 Marks)
ii) The time they met again (3 Marks)
c) In triangle ABC, B=38°, C=48° and c= 18.8 cm. Solve for triangle ABC using the cosine rule
(7 Marks)
d) Give a circumscribed circle is such that a= 34cm, b= 20cm and A=48°. Find the size of the diameter of
the circumscribing circle.
(3 Marks)
e) Each of the interior angle of a regular polygon is x°, and each exterior angle is {x-36}°
Find the value of x (3 Marks)
Find the number of sides in the polygon (2 Marks)
QUESTION TWO
a) Using a well labeled diagram determine the Sine and cosine of special angles 30° and 60°. Leave your
answer in surd form (10 Marks)
b) Use the cosine rule derived to solve triangle ABC if a= 70cm, b= 40cm C= 64° (4 Marks)

QUESTION THREE
a) Derive the cosine rule (10 Marks)
b) Use the cosine rule derived in (a) above to solve for triangle PQR such that; q= 8 cm, r= 12 cm and P=
132°.
(7 Marks)
c) In triangle ABC, C= 90°, B= 23.3° and AC= 11.2 cm. Find AB. (3 Marks)
QUESTION FOUR
a) A man standing on top of a cliff 1200m high is in line with two boats at the coastline whose angles of
depression are 18° and 25°. Calculate the distance between the two boats.
(6 Marks)
b) A flag post is 15 m high, if it casts a shadow with a length of 9.741m, determine the altitude of the sun
(4Marks)
c) Two aircrafts fly at 480 knots from x(0°, 2°W) to Y(30°N, 28°E). One flies along the equator and then
due north along the meridian 28°E. The other flies first due north and then due east along a parallel of
latitude 30°N. If the aircrafts leaves X the same time, find the difference in their arrival times at Y.
(10 Marks)
QUESTION FIVE
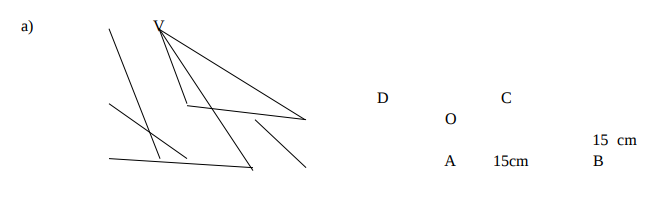
The figure above shows a pyramid VABCD with a square base of 15cm and each of its slanting
edge 20 cm long. O is the center of the base. Calculate:
i) The length of OB (5 Marks)
ii) The height VO (5 Marks)
iii) The angle between VB and the base (5 Marks)
iv) The angle between the plane VAB and the base (5 Marks)
