
2021 Physics paper 1
SECTION A
Answer all the questions in this section in the spaces provided.
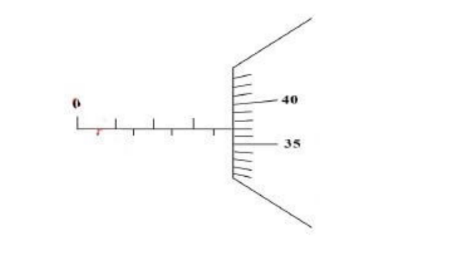
1. Figure 1 shows part of the thimble scale of a screw gauge with 50 divisions.
On the diagram, draw the sleeve scale to show a reading of 3.87 mm. (1 mark)
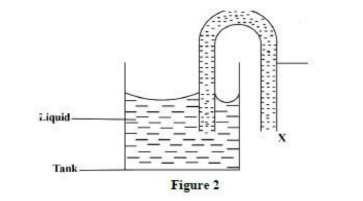
2. Figure 2 shows a siphon used to empty a tank. In order to start the siphon, state why:
a. it must be full of liquid. (1 mark)
- To overcome atmospheric pressure inside the siphon by expelling trapped air inside the siphon.b. end X must be below the level of the liquid in the tank. (1 mark)
- To create pressure difference.
- 3. Figure 3(a) shows a horizontal tube containing air trapped by a mercury thread of length 5 cm. Thelength of the enclosed air column is 7.5cm. The atmospheric pressure is 76 cmHg.
The tube is then turned vertically with its mouth facing down as shown in Figure 3(b).
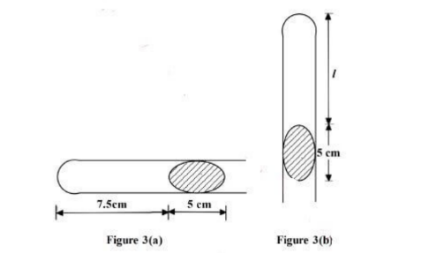
- a. Determine the length 1 of the air column. (3 marks)P1V1 = P2V2
76 x 7.5 = (76 – 5)l
l = 8.03cm (2 dp)
b. State the reason why the mercury thread did not fall out in Figure 3(b). (1 mark)
4. In a Physics experiment, a student filled a burette with water up to a level of 15 ml. The student ran out 3 drops of water each of volume 2 cm³ from the burette into a beaker. Determine the final reading of the burette. (2 marks)
Initial burette reading = 15ml
Volume of water dropped out = 3 drops x 2cm³
= 6cm³
New burette reading = 15cm³ + 6cm³
= 21cm
5. State two factors that affect the angular velocity of a body moving in a circular path (marks)
- The instantaneous linear velocity of the moving body
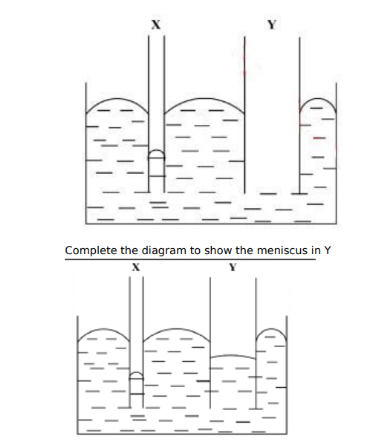
- The radius of the circular path6. Figure 4 shows two capillary tubes X and Y of different diameters dipped in mercury.
Complete the diagram to show the meniscus in Y. (1 mark)
- 7. In an experiment, a drop of black ink is introduced at the bottom of a container filled with water. It is observed that the water gradually turns black. State the effect on the observation when the experiment is carried out using water at a lower temperature. (1 mark)8. Figure 5 shows two identical springs arranged side by side and supporting a weight of 50 N.
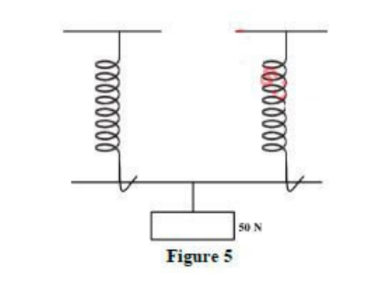
- When the same weight is supported by one of the springs above, it produces an extension of 1 cm.Determine the effective spring constant of the arrangement in Figure 5. (3 marks)
K = F/e = 50N/1cm
= 50N/cm
KT = 2x 50N/cm
= 100N/cm or 1000N/m
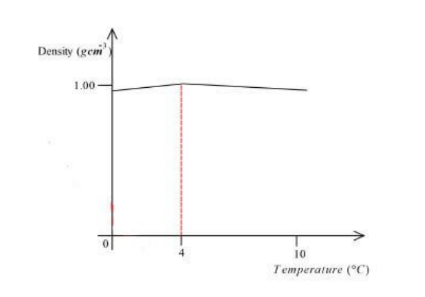
9. On the axes provided, sketch a graph of density against temperature for water between 0°C and 10 °C. (1 mark)
- 10. State the reason why a student climbing a hill tends to bend forward. (1 mark)
- To shift the position of the centre of gravity to the front part to maintain equilibrium.11. Figure 6 shows a graph of temperature against time for a pure molten substance undergoing cooling.
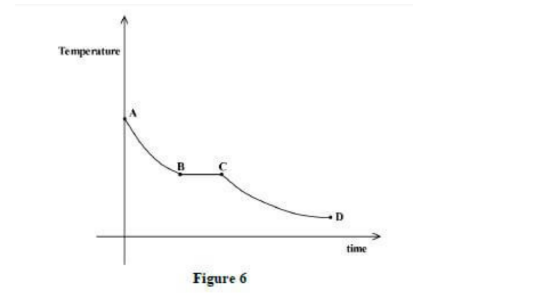
- Explain what happens to the substance in region BC. (2 marks)
- The substance undergoes change of state from molten to solid without change in temperature.12. Figure 7 shows a uniform rod AB 2 m long and of mass 1 kg. It is pivoted 0.5 m from end A and balanced horizontally by a string attached 0.1 m from end B.
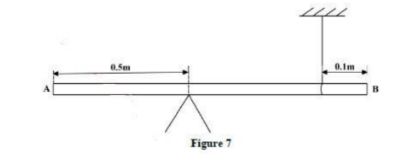
- Determine the tension in the string. (take g = 10 Nkg) (2 marks)Sum of clockwise moments = sum of anti-clockwise moments
10N × 0.5m = 1.4m × T
T= 3.57N
13. Figure 8 shows two pieces of ice A and B trapped using a wire gauze in a large beaker containing water. Heat is supplied at the centre of the base of the beaker as shown. State the reason why B melted earlier than A (1 mark)
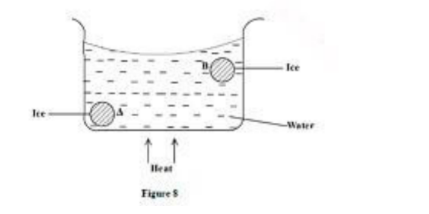
- Heated water at the bottom becomes less dense which rises to the top. Hence ice B melts earlier than A.14. Figure 9 shows a folded piece of paper. A stream of air is blown underneath the paper.
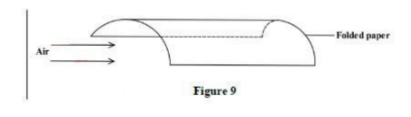
- Explain why the paper collapsed. (2 marks)Air blown underneath the paper reduces pressure acting on the paper. Atmospheric pressure acting from top becomes higher. Hence the paper collapses.
SECTION B (55 marks)
Answer all the questions in this section in the spaces provided.
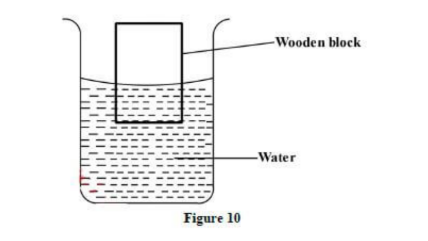
15.a. Figure 10 shows a wooden block of volume 90 cm floating with 1/3 of its body submerged inwater of density 1gcm-3 (g = 10 Nkg-1)
- Determine:i. The weight of the block
weight of block = vpg
1/3 x 90 x 1000 x 10
100000
= 0.3N
Alternatively
W = mg
m = 1/3 x 90 x 1
= 30g
W = 30 x 10
1000
= 0.3N
ii. The weight of a metal block that can be placed onto the block so that its top surface is on the same level as the water surface.(3 marks)
Volume of remaining part = 90 – 30 = 60cm3 U → W = vpg
= 60/1000000 x 1000 x 10
= 0.6N
w = mg but m = v x p
60 x 1 = 60g
w = 60/1000 x 10
= 0.6N
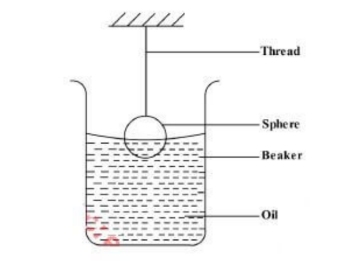
b. Figure 11 shows a solid metal suspended in oil using a thread.
- i. Other than upthrust, list two other forces acting on the sphere. (2 marks)
- Tension force
- Weight, mgii. The oil is carefully and gradually drawn from the beaker. State the effect on each of the two forces in 15(b)(i). (2 marks)
- Tension force will increase
- Weight, mg, will remain constant16.a. Define the term “specific latent heat of fusion” (1 mark)
Quantity of heat required to change a unit mass of the material from solid state to liquid without change in temperature.
b. Ice of mass 5g at a temperature of -10°C is immersed into 10.5g of hot water at 100°C in a container of negligible heat capacity.
All the ice melts and the final temperature of the mixture is 40°C. Assuming there are no heat losses to the surrounding and taking the specific latent heat of fusion for ice as L (Cwar = 4200 Jkg-K and C = 2100 Jkg ‘K).
Determine the:
i. heat lost by the hot water. (3 marks)
heat lost by the water. (3 marks)
Heat lost by the water = m<subw< sub=””>c<subw< sub=””>Δθ</subw<></subw<>
0.0105 x 4200 x (100 – 40)
= 2646J
ii. heat gained by ice from -10°C to 0°C. (2 marks)
heat gained by ice from −10°C to 0°C
heat gained by ice upto 0oC = miceciceΔθ
iii. heat required to melt the ice in terms of Lf (1 mark)
heat required to melt the ice in terms of Lf (1 mark)
mLf
0.005Lf
iv. heat gained by the melted ice. (2 marks)
heat gained by the melted ice. (2 marks)
heat gained by melted ice upto = miceciceΔθ
0.005 x 4200 x 40
= 840J
v. specific latent heat of fusion of ice. (3 marks)
heat lost by hot water= heat gained by ice(-10oC to 0oC) + melting ice + melted ice up to 40oC
2646J = 105J + 0.05Lf + 840J
17. Figure 12 shows a hydraulic lift system. The radius of the small piston is 5.64 cm while that of the large piston is 14.24 cm. The small piston is operated using a lever. A force of 100N is applied to the lever
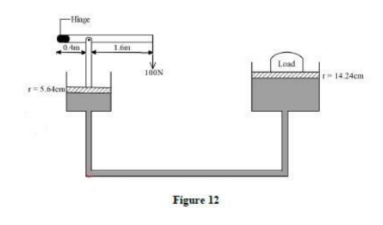
- Determine the:a. pressure exerted by the smaller piston. (5 marks)
w x 0.4 = 100N x 2.0m
w = 500N
P = F/A but A = πr2
22/7 x 5.642
= 99.97cm2
= 99.97 x 10-4m2
P = 500N
99.97 x 10-4m2
=5.0015 x 104Pa
b. load that can be lifted. (3 marks)
L = P x Alarger piston
5.0015 x 104 x 22/7 x 14.242 x 10-4m²
c. mechanical advantage of the system. (3 marks)
M.A = Load/Effort
3185.22N/500N
= 6.37
18.a. A bus moving initially at a velocity of 20ms-1 decelerates uniformly at 2 ms-2
i. Determine the time taken for the bus to come to a stop. (3 marks)
t =v – u OVER a
= 0 – 20 OVER 2
= 10sec
ii. Sketch the velocity – time graph for the motion of the bus up to the time it stopped. (2 marks)
iii. Use the graph to determine the distance moved by the bus before stopping. (1 mark)
Distance = Area under the curve
1⁄2 x 20 x 10
= 100m
b. A car of mass 1000 kg travelling at a constant velocity of 40ms-1 collides with a stationary metal block of mass 800 kg. The impact takes 3 seconds before the two move together.
Determine the impulsive force. (4 marks)
m1v1 + m2v2 = v(m1 + m2)
(1000 x 40) + (800 x 0) = v(1000 + 800)
= 22.22m/s
v = u + at
22.22 = 40 + 3a
a = -5.93m/s²
(decelerating)
F = ma
1800 x -5.93
= 10674N
19.a. State two conditions necessary for a body to be in equilibrium. (2 marks)
- Sum of clockwise moments about a point must be equal to the sum of anti- clockwise moments about the same point.
- For a system of parallel forces in equilibrium, sum of forces in either direction is equal.b. Figure 13 shows a non-uniform log of wood AB of length 4m. The log is held horizontally by applying forces of 80N at end A and 120N at end B.
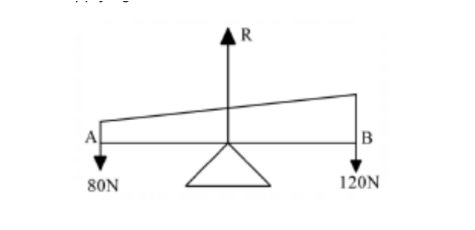
- Determine:i. the value of R. (1 mark)
the value of R. (1 mark)
R = 80 + 120
= 200N
ii. the position of the centre of gravity of the log from end B. (3 marks)
Let x be the distance from the pivot to point B
80(4 – x) = 120x
320 = 200x
x = 1.6m
c. You are provided with a metre rule, a knife edge and a mass m1
i. Describe how the position of the centre of gravity of the metre rule can be determined using the knife edge. (2 marks)
Place the metre rule horizontally on knife edge. The position where it balances on the knife edge is the centre of gravity.ii. Using the position of the centre of gravity determined in 19(c)(i) and the mass M,describe how the mass M of the metre rule can be determined. (4 marks)
- Move the knife edge away from the centre of gravity to a new position. Note the distance from the knife edge and the centre of gravity as d1
- Place the mass m1 on one side of the metre rule and adjust it until the rule balances as in 19 c (i). Note the distance from the knife edge and the mass m1 as d2.
- Using principle of moment;Md1 = m1d2
M = m1d2/d1
Where M is the mass of the metre rule
