
2021 Mathematics Paper 1
Section I (50 marks)
Answer all the questions in this section.
1. Evaluate 1⅘ ÷ ⅔ of 2¼ -3/10 OVER 5/6 + 22/39 + 1 2/11
2. Two bells ring at intervals of 35 and 42 minutes respectively. The bells ring together at 8.48 a.m.
Determine the time when the bells will ring together again. (3 marks)
3. Complete the figure below to show a rotational symmetry of order 3 about O. (3 marks)

4. Solve 5/3 -2x <1 – 2/3x ≤ 2 – x. Hence list the integral values that satisfy the inequalities. (3 marks)
5. The size of two interior angles of an irregular polygon each measures 90°. All the other remaining interior angles each measure 150°. (3 marks)
Determine the number of sides of the polygon.
6. In a race Kipsang maintained an average speed of 5 m/s. When he was 310 m to the finishing line,Mutunga was 50 m behind him. However, Mutunga finished the race 10 m ahead of Kipsang.
Determine Mutunga’s average speed. (3 marks)
7. Simplify (4 + 2y)²– (2y – 4)²(2 marks)
8. A table is sold at Ksh 4 500 and a chair at Ksh 2 000. A salesman earns a commission of 8% on every table and 5% on every chair sold. On a certain week, he sold 3 more chairs than tables and his total earnings were Ksh 3 980.
Determine the number of chairs he sold that week. (3 marks)
9. A translation T maps A(-6, 2) onto A'(3,5).
a. Determine the translation vector T.
b. A point P'(-4, 2) is the image of P under T. Determine the coordinates of P. (2 marks)
10. The cost of one litre of Petrol is Ksh 110. John’s vehicle covers 12 km on one litre of petrol.
He used Ksh 2 805 on petrol to travel from town A to town B. Jane’s vehicle consumes 12.5 litres of Petrol for every 100 km travelled.
Calculate the amount of money that Jane would use to travel from town A to B on the same road.(3 marks)
11. Solve for θ
sin (2θ -15) = cos 3θ(2 marks)
12. Line AB drawn below is a side of a trapezium ABCD.

a. Using a ruler and pair of compasses only, complete trapezium ABCD in which AB is parallel to DC,∠BAD= 67.5°, AD = 5 cm, BC = 5.5 cm and ∠ABC is acute. (3 marks)
b. Measure the length of DC. (1 mark)
13. Ali left Mombasa for Nairobi on Tuesday at 2.30 a.m. He arrived in Mtito Andei after 3 hours 12 minutes.
He stayed in Mtito Andei for 36 hours and then left for Nairobi. He took 5 hours 25 minutes to arrive in Nairobi.
Determine the day and time in the 12 hour system Ali arrived in Nairobi. (3 marks)
14. The height of a cone is 12 cm. A frustrum whose volume is one eighth the volume of the cone is cut off. Determine the height of the frustrum. (3 marks)
15. Solve the equation 8x+1 – 23x-1 = 120. (4 marks)
16. A curve is given by y=2x³- 3x² – 12x + 12.
a. Find the gradient function of the curve. (1 mark)
b. Determine the equation of the normal to the curve at the point (1,-1), in the form y = mx + c, where m and c are constants. (3 marks)
SECTION II (50 marks)
Answer only five questions in this section in the spaces provided.
17. A factory packs fruit jam in cylindrical tins of radius 5 cm and height 15 cm. The tins are then packed into rectangular cartons each measuring 60 cm long, 30 cm wide and 30 cm high.
a. Determine the maximum number of tins that can be packed in one carton. (2 marks)
b. An empty carton and an empty tin weighs 560 g and 300 g respectively. The jam packed in one tin weighs 990 g. A pick-up which can carry a maximum of 600 kg is used to transport
the jam.
Determine the maximum number of cartons the pick-up can carry. (4 marks)
c. The factory delivered a pick-up full of cartons of jam to a retailer. The factory sells one carton to a retailer for Ksh 2 880.
The retailer sells each tin at Ksh 110.
Calculate the percentage profit made by the retailer. (4 marks)
18.a. The length of each side of an equilateral triangle ABC is 10 cm. Calculate the area of the triangle, correct to 2 decimal places. (2 marks)
b. Triangle ABC in 18(a) forms the base of a solid triangular pyramid VABC. The perpendicular height of the pyramid is 15 cm.
Calculate the volume of the pyramid. (2 marks)
c. The pyramid VABC in 18(b) above is recast into a cone of base radius 3.5 cm.
Calculate, correct to 2 decimal places:
i. the height of the cone; (2 marks)
ii. the surface area of the cone. (4 marks)
19. Elimu School bought 25 textbooks and 35 exercise books for Ksh 13 500 from bookshop A. From the same bookshop Soma School bought 21 textbooks and 38 exercise books and spent Ksh 1 300 less than Elimu School.
Take x to represent the price of a textbook and y to represent the price of an exercise book.
a. Form two equations representing the above information. (2 marks)
b. Use matrix method to determine the price of each item. (5 marks)
c. In bookshop B, the cost of a textbook was 5% less and that of an exercise book was 5%
more than in bookshop A. Kasuku School bought the same number of textbooks and
exercise books as Elimu School in bookshop B.
Calculate the difference in the amount spent by Kasuku School and Elimu School (3 marks)
20. The figure below is a quadrilateral ABCD in which AB=8 cm, BC= 6 cm, CD = AD, ∠ABC = 70° and ∠ADC = 50°.
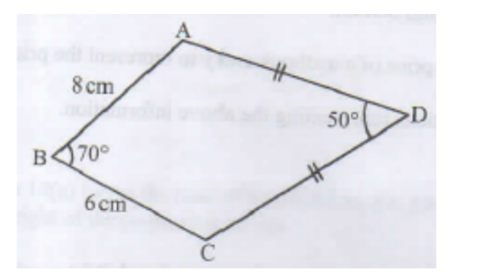
a. Calculate, correct to one decimal place:
i. the length AC. (2 marks)
ii. the length DC. (2 marks)
iii. the size of angle BAD. (3 marks)
b. Calculate the area of the quadrilateral ABCD, correct to one decimal place. (3 marks)
21.a. Solve for x
(x-4)²= (x-8)(2x + 7).
b. John cycled 6 km from his home to school at an average speed of (2x – 3) km/h.
Peter walked 2.4 km from his home to the school at an average speed of x km/h. Peter took 16 minutes less than John.
Determine the time, in minutes, that John took to reach the school. (6 marks)
22. The position vectors of A and B are (-4 6) and (-8 2) respectively.
Point M is the midpoint of AB and point N is the midpoint of OA.
a. Find:
i. the vector AB. (2 marks)
ii. the coordinates of points M and N. (2 marks)
iii. the magnitude of NM. (3 marks)
b. The coordinates of a point C is (2, a). Vector CA is parallel to vector OB.
Determine the value of a. (3 marks)
23. The masses of 40 adults who attended a health clinic were recorded as follows.
64 58 52 73 62
50 60 64 49 47
58 45 58 74 66
73 48 46 55 52
51 69 59 44 60
42 48 54 73 61
58 50 41 53 54
46 43 61 67 70
a. Complete the frequency distribution table below for the above information. Use classes of size 5 starting with the class 40 – 44.(4 marks)
| Mass (kg) | Frequency (f) | Mid points (x) | fx | cf |
|---|---|---|---|---|
| 40 -44 |
b. State the modal class. (1 mark)
c. Estimate:
i. the mean mass. (2 marks)
ii. the median mass. (3 marks)
24. The equation of a curve is given as y = 1/3x3– 1/2x2 – 2x – 1/3
a. Find:
i. the value of y when x=-2. (2 marks)
ii. the equation of the tangent to the curve at x = -2. (4 marks)
b. Determine the coordinates of the turning points of the curve. (4 marks)
