
2020 Mathematics Paper 1
Section I (50 marks)
Answer all the questions in this section.
1. Without using mathematical tables or a calculator, evaluate –3(6 + –2) – –12 ÷ 4 + 5
–4 x –6 + –3 x 5(3 marks)
2.Express 5.5 as a mixed number (1 mark)
3. 3. Without using a calculator or mathematical tables, evaluate: (3 marks)
493/2x{256/2401}¾
4. A rectangular floor of a room measures 5.4 m long and 4.2 m wide. The room is to be covered with square tiles. Calculate the minimum number of square tiles that can be used to cover the floor.(4 marks)
5. Simplify 2x² – xy – 6y²
x² – 4xy + 4y²(3 marks)
6. The line 2y+x= 1 is perpendicular to a line L. Line L passes through point (2,−1), Determine the equation of L in the form y = mx + c, where m and c are constants. (3 marks)
7. The sum of the interior angles of a regular polygon is 12600. Find the size of each exterior angle of the polygon.(3 marks)
8. Using the grid provided below, solve the simultaneous equations.
x – 4y = -5
–x + 2y = 1 (3 marks)
9. Given that sin(θ+30°)=cos2θ, find the value of cos(θ+40°). (3 marks)
10. In the figure below, AB and CD are arcs of two concentric circles, centre O. Angle AOB = 60° and AD=BC=7cm.
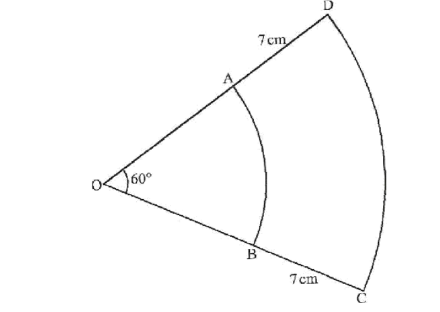
Given that the perimeter of ABCD is 28 2/3 cm, find OA, the radius of the inner circle. (3 marks)
11. Using a ruler and a pair of compasses only, construct a parallelogram ABCD in which AB = 6cm, BC = 5cm and angle ADC = 150°.(3 marks)
12. A Kenyan Non-Governmental Organization (NGO) received a donation of 200 000 US dollars.
The money was converted into Kenyan shillings in a bank which buys and sells foreign currency as follows:
| Buying (Ksh) | Selling (Ksh) | |
|---|---|---|
| 1 USD Dollar | 102.40 | 102.50 |
| 100 Japanese Yen | 92.80 | 93.30 |
(a) Calculate the amount of money, in Kenya Shillings, the NGO received. (1 mark)
(b) The NGO used 90% of the donation to buy a machine from Japan. Calculate the cost of the machine to the nearest Japanese Yen. (3 marks)
13. A chord of a circle, 7 cm long subtends an angle of 60° at the centre of the circle. Determine the area correct to 2 decimal places, of the major segment of the circle. (4 marks)
14. A vertical electric pole was erected 6.4m from the foot of a vertical fencing pole on the same horizontal level. The fencing pole is 2m high.
The angle of elevation of the top of the electric pole from the top of the fencing pole is 30°. Determine the height of the electric pole correct to 1 decimal place. (2 marks)
15. In a 4×400 m relay competition, a team of athletes each completed their round in 45 sec, 43 sec, 44 sec and 45 see respectively.
If the race started at 1:35:31 p.m., find the time when the team completed the race. (3 marks)
16. The figure below shows a quadrilateral ABCD and a mirror line M1M2.
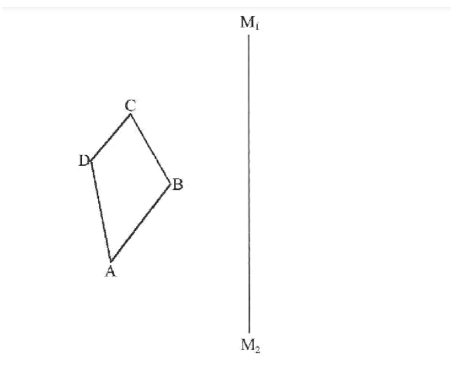
(a) Draw quadrilateral A’B’C’D’, the image of ABCD, under a reflection in the mirror line M1M2.(2 marks)
(b) State the type of congruency between ABCD and A’B’C’D’.(1 mark)
SECTION II (50 marks)
Answer any five questions from this section in the spaces provided.
17. Three business partners, Kosgei, Kimani and Atieno contributed Ksh 1,750,000 towards an investment.
Kosgei contributed 20% of the money.
Kimani and Atieno contributed the remainder in the ratio 3:5 respectively.
(a)(i) Calculate the amount of money Kimani contributed.(2 marks)
(ii) Find the ratio of the contributions by the three partners.(2 marks)
(b) The money earned a compound interest at a rate of 8% per annum. After 3 years, the partners withdrew the interest and donated 10% to a charitable organisation.
The partners then shared the remainder in the ratio of their contributions.
Calculate the amount of money, to the nearest shilling, that each partner received.(6 marks)
18. A solid consists of a conical part, a cylindrical part and a hemispherical part. All the parts have the same diameter of 12cm.
The height of the cylindrical part is 15cm and the slanting height of the conical part is 10 cm. (Take π = 3.142).
Calculate the:
(a) height of the solid;(2 marks)
(b) surface area of the solid, correct to 1 decimal place,(4 marks)
(c) volume of the solid, correct to 1 decimal place. (4 marks)
19. The average speed of a pick-up was 20km/h faster than the average speed of a lorry. The pick-up took 45 minutes less than the lorry to cover a distance of 180 km.
(a) If the speed of the lorry was x km/h:
(i) Write expressions in terms of x for the time taken by the lorry and the pick-up respectively to cover the distance of 180 km(2 marks)
(ii) Determine the speed of the lorry and that of the pick-up.(5 marks)
(b) The distance between towns A and B is 240 km. On a certain day the pick-up started from town A at 8.30 a.m. and the lorry started from town B at the same time.
Determine the time that the lorry and the pick-up met. (3 marks)
20. A forest is enclosed by four straight boundaries AB, BC, CD and DA. Point B is 25km on a bearing of 315° from A, C is directly south of B on a bearing of 260° from A and D is 30km on a bearing of 210° from C.
(a) Using a scale of 1:500,000, represent the above information on a scale drawing (3 marks)
(b) Using the scale drawing, determine the:
i. distance, in kilometres, of D from A: (2 marks)
ii. bearing of A from D (1 mark)
(c) Calculate the area, correct to 1 decimal place, of the forest in square kilometres. (4 marks)
21. The position vectors of points A and B are
OA={2/4} and OB={12/-4}
A point M is on AB such that AM = 1⁄2AB and a point N is on OB such that ON:NB= 1:3.
(a) Find:
(i) AB(2 marks)
(ii) NM;(3 marks)
(iii) |NM|, correct to 1 decimal place. (2 marks)
(b) A translation vector maps A onto A'(5,−1). Find the coordinates of the image of B under the translation vector.(3 marks)
22. The number of students in 40 schools in a certain sub-county were recorded as follow:
238 100 173 115 398 597 572 299
255 750 587 403 250 217 797 386
362 486 453 279 436 248 780 316
529 305 372 286 842 235 420 492
226 245 695 720 267 617 198 830
(a) Complete the frequency distribution table below for the data.
| Number of students | 100-199 | 200-249 | 250-399 | 400-599 | 600-799 | 800-849 |
|---|---|---|---|---|---|---|
| Number of schools |
(a) Complete the frequency distribution table below for the data.
(b) On the grid provided, draw a histogram to represent the data.(4 marks)
(c) Use the histogram to estimate the:
(i) median; (2 marks)
(i) number of schools with more than 350 students. (2 marks)
23. (a) Given that matrix is a singular matrix, find the value of p. (3 marks)
(b) Kirai earned a basic salary of Ksh x per month and Ksh y for each extra hour worked.
Mutua’s basic salary is 20% more than Kirai’s basic salary but also earns Ksh y for each extra hour worked.
In a certain month, Kirai worked 30 extra hours and earned a total of Ksh 70,000 while Mutua worked an extra 40 hours and earned a total of Ksh 88,000.
(i) Form two equations in x and y to represent Kirai’s and Mutua’s total earnings. (2 marks)
(ii) Use matrix method to solve for x and y.(5 marks)
24. The displacement, s metres, of a moving particle after t seconds is given by S=2/3t3-7/2t2-6t+8
Determine the:
(a) velocity of the particle when t = 5:(3 marks)
(b) time, t seconds, when the particle is momentarily at rest; (3 marks)
(c) displacement, s metres, when the particle is momentarily at rest; (2 marks)
(d) acceleration of the particle when t = 4 seconds.(2 marks)
