
Kenya Certificate of Secondary Education
2019 Mathematics Paper 2
1. Simplify √5+3∕ √5-2 . Give the answer in the form a + b∕c where a, b and c are integers. (2 marks)
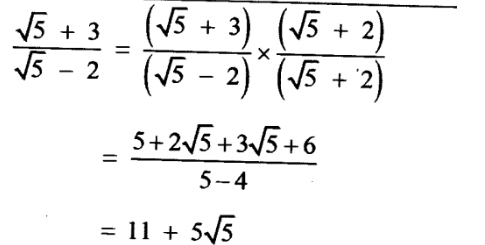
2. Two types of flour, X and Y, cost Ksh 60 and Ksh 72 per kilogram respectively.
The two types are mixed such that the cost of a kilogram of the mixture is Ksh 70. Calculate the ratio X:Y of the mixture.(3 marks)
Let the ratio of X to Y = x: y
60x + 72y/x + y = 70
60x + 72y = 70x + 70y
l0x = 2y x/y = 2/10 0r 1/5
∴ Ratio X:Y = 1:5
3. A quantity P varies inversely as the square of another quantity L.
When P = 0.625, L = 4. Determine P when L — 0.2. (3 marks)
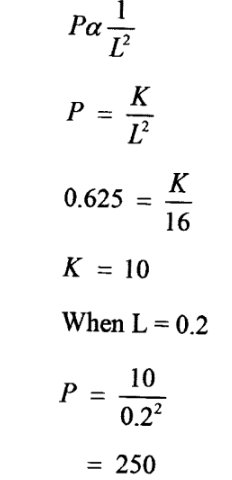
4. An arc of a circle subtends an angle of 150° at the circumference of the circle.
Calculate the angle subtended by the same arc at the centre of the circle. (2 marks)
Angle at centre = 2 x 150°
= 300°
5. Solve the equations:
x + 3y = 13
x² + 3y² = 43 (4 marks)
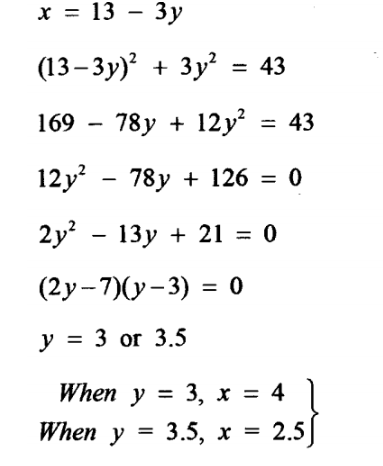
6. A bag contains 6 red counters and 4 blue counters.
Two counters are picked from the bag at random, without replacement.
(a) Represent the events using a tree diagram. (1 mark)
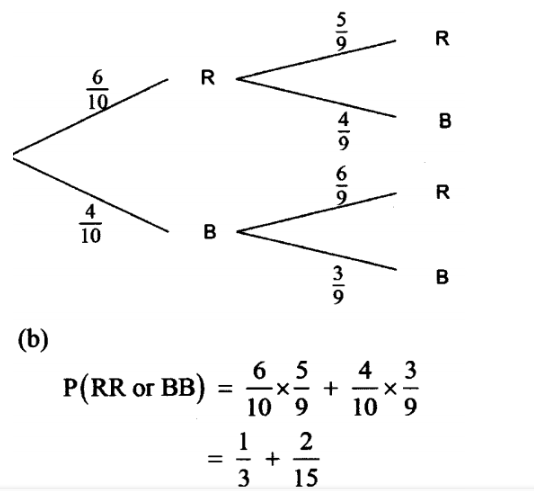
(b) Find the probability that the two counters picked are of the same colour. (2 marks)
P(RR or BB) = 6/10 X 5/9 X 4/10 X 3/9
= 1/3 + 2/15
7/15
7. Find the coordinates of the turning point of the curve y=x²-14x+10 (3 marks)
dy/dx = 2x -14
At the turning point
dy/dx = 2x — 14 = 0
x = 7
y = 49 — 98 + 10 = —39
Coordinate of turning point — (7, —39)
8. OAB is a Sector Of a circle of radius r cm. Angle AOB = 60°.
Find, in its simplest form, an expression in terms of r and z for the perimeter of the sector.(2 marks)
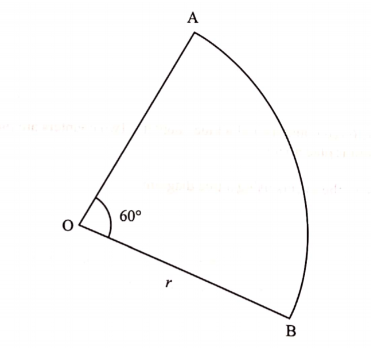
Perimeter of sector = 60/360 x 2π + 2r
= 2r x 1/3πr
9. In a mathematics test, the scores obtained by 30 students were recorded as shown in the table below.
| Score (x) | 59 | 61 | 65 | K | 71 | 72 | 73 | 75 |
|---|---|---|---|---|---|---|---|---|
| No. of students | 2 | 3 | 5 | 6 | 7 | 4 | 2 | 1 |
The score K with a frequency of 6 is not given.
Given that ⅀fd∕⅀f = — 1.2 where d —— x – 69, and using an assumed mean of 69, determine score K.
| Score x | No. of Students | d = x – 16 | fd |
|---|---|---|---|
| 59 | 2 | -10 | -20 |
| 61 | 3 | -8 | -24 |
| 65 | 5 | -4 | -20 |
| k | 6 | k-16 | 6(K-69) |
| 71 | 7 | 2 | 14 |
| 72 | 4 | 3 | 12 |
| 73 | 2 | 4 | 8 |
| 75 | 1 | 6 | 6 |
| Σf =30 | |||
Σfd/Σf 6k — 438/30 = 1.2
6k = 402
k = 67
10. Determine the amplitude and the period of the function y = 3 sin(2x + 40°). (4 marks)
Amplitude = 3 Period = 360/2 =180°
11. The figure ABCDEFGH represents a box.
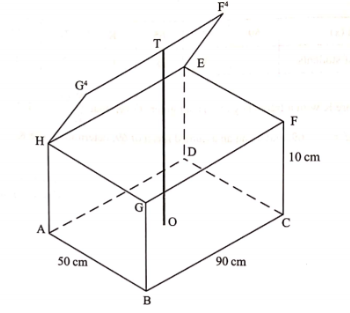
The top lid of the box is opened such that the height OT is 35cm. Calculate the:
(a ) angle the top lid makes with the plane FGHE;
Sin θ = 25/50 θ Sin<sup-1< sup=””>(1/2) = 30°</sup-1<>
(b) length BE, correct to 2 decimal places.
BE = √(90²+50²+10²)
= √10700
=103.44
12. The table below’ shows income tax rates in a certain year.
| Monthly Income in ksh | Tax rate in each shilling (%) |
|---|---|
| 0 – 10164 | 10 |
| 10165 – 19740 | 15 |
| 19741 – 29316 | 20 |
| 29317 – 38892 | 25 |
| 38893 and above | 30 |
In that year,mawira earned a salary of 41000 per month.
calculate mawira’s income tax per month given that a monthly tax relief of ksh 1162 was allowed (3 marks)
Tax before relief
10164 x 0.1 + 9576 x(0. 15 + 0.2 0 25)
+2l08 x 0.3
= 7394.4
Net tax = Ash (7394.4 1162)
= Ksh 6232.4
13. The position vectors of points A,B and C are OA =[3/4],OB = [1/2] and OC =[7/-1] show that A,B and C are collinear (3 marks)

14. The vertices of a triangle PQR are P(-3, 2), Q(0, — 1) and R(2, — 1). A transformation matrix maps triangle PQR onto triangle P’Q’ R’ whose vertices are P'(—7, 2), Q'(2, — 1) and R’(4, – 1).
Find M1 the transformation that maps P’Q’R’ onto PQR.(4 marks)
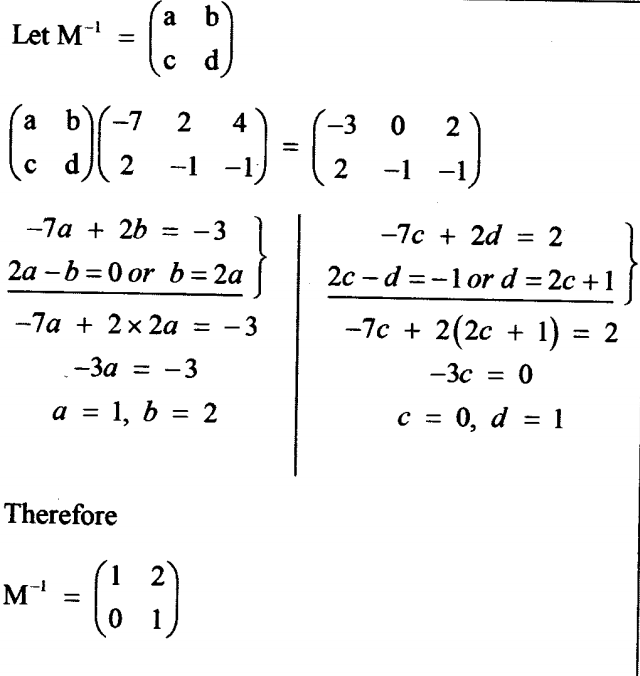
15. Solve for x in log(7x—3) + 2 log 5 = 2 + log(x + 3).(4 marks)
2 = log 100
log (7x — 3) + log 5² = log 100 + log(x + 3) log )25(7x — 3)) = log (100(x + 3))
25(7x — 3) = 100(x + 3)
7x — 3 = 4x + 12
3x = 15
x = 15
16. The length of a shadow’ of a mast was measured at intervals of 1 hour and recorded as shown in the table below.
| Time( hr) | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Length( m) | 18.7 | 8.7 | 5.0 | 2.9 | 1.3 | 0 |
(a) On the grid provided, draw the graph of length against time. (2 marks)
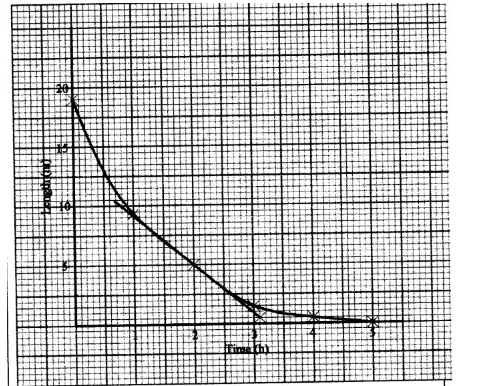
(b) Determine the rate of change of the shadow’ length at = 2 (2 marks)
Acceptable tangent drawn at = t = 2
Tangent passes through points
(2, 5) and (2.5, 3.5)
3.5 — 5/2.5 — 2 = -1.5/0.5
= -3.0m/s
SECTION II (50 MARKS)
Answer any five questions
17.The first term of an Arthmetic Progression(AP) is equal to the first term of a Geometric Progression (GP).
The second team of the AP is equal to the fourth term Of the GP while the tenth term of the AP is equal to the seventh term of the GP.
(a) Given that a is the first term and d is the common difference of the AP while r is the common ratio of the GP, write the two equations connecting the AP and the GP. (2 marks)
ar³ = a + d
ar6 a + 9d
(b) Find the value of r that satisfies the progressions.(4 marks)
From (a) above d = ar3 -a
a +9(ar3 -a) = ar6
a +9ar3 -9a = ar6
ar6 -9ar3 +8a = 0
r6 -9r3 +8 = 0
(r3-1)(r3-8) = 0
r = 1 or r = 2
r = 2
(c) Given that the tenth term of the GP is 5120, find the values of a and d.(2 marks)
ar9 = 5120
a = 5120/2/sup>=10
a+d = 10 x 2³ = 80
∴ d = 80 – 10 = 70
(d) Calculate the sum of the first 20 terms of the AP.( 2 marks)
S 20 20/2(20 +19 x 70)
=13500
18. Mbaka bought some plots at Ksh 400000 each. The value of each plot appreciated at the rate of 10% per annum.
(a) Calculate the value of a plot after 2 years. (2 marks)
558 400 = 400 000(1.1)t
1.1=t558 400/400 000
1.1t = 1.396
t log 1.1 = log 1.396
log1.396/log1.1 = 3.500
= 3 years 6 Months (or 42 months)
(b) After some time t, the value of a plot was Ksh 558400. Find i, to the nearest month. (4 marks)
Value of a plot after 2 years>
= 400 000 x I .1²
= Ksh. 484 000
(c) Mbaka sold all the plots he had bought after 4 years for Ksh2 928200.
Find the percentage profit Mbaka made, correct to 2 decimal places. (4 marks)p> Let the number of plots bought be x
x x 400 000 x(1.1)4 = 2 928 200
2 928 200/400 000 x(I.l)4 = 2 928 200/585 640
= 5
Profit = 2 928 200 — 5 x 400 000
= 928 200
%profit =( 928 200/2 000 000) x100% = 46.41
19. The figure KLMN below is a scale drawing of a rectangular piece of land of length KL = 80m

(a) On the figure, construct
(i) The locus of a point P which is both equidistant from points L and M It and from lines KL and LM. (3 marks)
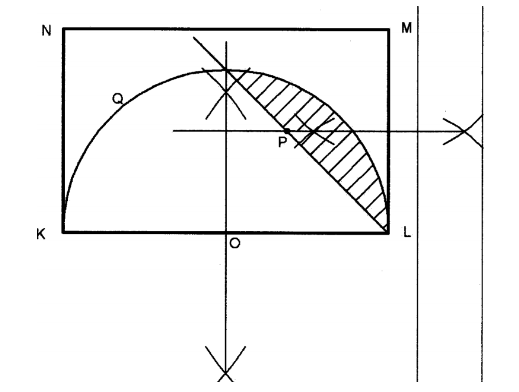
bisector to line LM
Bisector to HKLM
Position of P correctly identified
(ii) the locus of a point Q such that ∠KQL = 90°. (3 marks)
bisector to line KL Correct centre used
Locus of Q correctly drawn
(b) (i) Shade the region R bounded by the locus of Q and the Locus of points equidistant from KL and LM. (3 marks)
(ii) Find the area of the region R in m². (Take ℼ= 3.142). (3 marks)
r = 40m
Area of region R
90/360 x 3.142 x 40²x – 1/2 x 40 x 40
= 1256.8 – 800
= 456.8m²
20. A ship left point P(l0°S, 40°E) and sailed due East for 90 hours at an average speed of 24 Kms to a point R.
(Take I nautical mile (nm) to be 1.853 km and radius of the earth to be 6370 km)
(a) Calculate the distance between P and R in:
(i) nm; (1 marks)
= 24 x 90
‘ 2160nm
(ii) km. (1 marks)
= 2160 x 1.853
= 4002.48 km
(b) Determine the position of point R.( 5 marks)
I° = 60 cos10 nm
0 = <po,r
0 2160/60cos10</po,r
= 36.56°
Position of R
(10°S, (40 + 36.56)°E)
– (10°S, 76.36°E)
(c) Find the local time, to the nearest minute, at point R when the time at P is II:00a.m. (3 marks)
Longitude difference between P and R = 36.56°
Time difference = 36.56 x 4
=2hrs 26mins
Local time at R
= 1100h + 2h 26min
= I 326h
= 1.26 pm
21. A workshop makes cupboards and tables using two artisans A and B every cupboard made requires 3 days of work by artisan A and 2 days of work by artisan B.
Every table made requires 2 days of work by artisan A and 2 days of work by artisan B.
In one month artisan A worked in less than 24 while artisan B Worked for Not More Than 18 Days.
The workshop made x cupboards and y tables in that month.
(a) Write all the inequalities which must be satisfied by x and y. (3 marks)
x ≥ a, y ≥ 0
2x + 2y ≤ 18 or x + y ≤ 9
3x + 2y < 24
(b) Represent the inequaliiies in (a) on the grid provided.(3 marks)
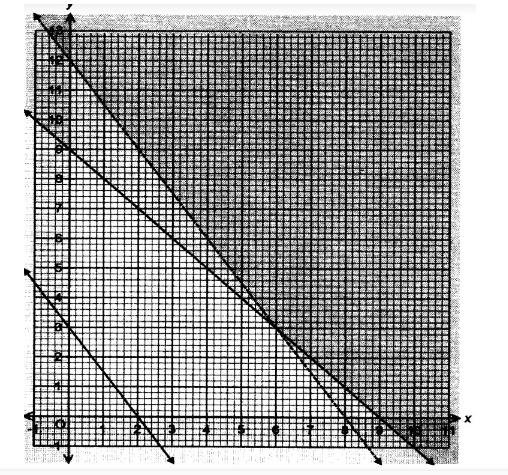
(c) The workshop makes a profit Of Ksh 6 000 on each cupboard and Ksh4 000 on each table.
Find the number of cupboards and the number of tables that must be made for maximum profit and hence determine the maximum profit. (4 marks)
Objective function
6000z + 4000y =12000 or 3 + 2y = 6
z = 5, y = 4 and z = 7, y = 1
Profit – sh (60fi0 x 5 + 40tD x 4) or (6000 x 7 + 4000 x 1)
=sh.31,600
22. The amount of money contributed by a group of students during a fundraising for a needy student was as shown in the table below.
| Amount( Ksh) | 301 – 400 | 401 – 500 | 501 – 600 | 601 – 700 | 701 – 800 | 801 – 900 | 901 – 1000 |
|---|---|---|---|---|---|---|---|
| No. of students | 2 | 10 | 12 | 14 | 7 | 3 | 2 |

(a) On the grid provided draw an ogive to represent the data. (4 marks)
(b) Use the graph to estimate:
(i) The median; (1 marks)
= Contribution of 25th student
= 605.5
(ii) The quartile deviation; (3 marks)
Q3 Contribution of 37.5 student
= 695.5
Q1 = Contribution of 12.5 student
= 505.5
Q3 — Q1/2 695.5 — 505/2
= 95
(iii) The percentage number of students who contributed at least Ksh 750.50. (2 marks)
= 9
% = 9/50 x 100
= 18%
23. In the figure below, OA = a,OB = b and BX meets OY at C.OX:OA = 1:2 and BY:YA = 1:3.
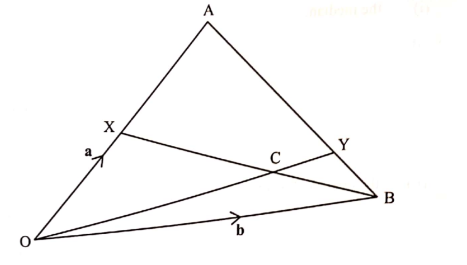
(a) Express in terms of a and b: (1 marks)
(i) BA = a – b
= 3/4b+1/4a
(ii) OY; (2 marks)
=b + 1/4(a-b)
(iii) BX. (1 marks)
BX = -b + 1/2a
(b) Given that OC = hOY and BC = kBX, determine the values of h and k. (6 marks)
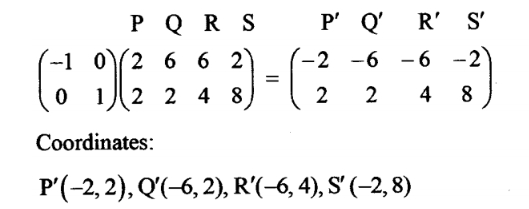
24. A trapezium PQRS with vertices P(2, 2), Q(6, 2), R(6, 4) and S(2, 8) is mapped onto P’Q’R’5′ by a transformation matrix M = (—1/0 0/1).
(a) Find the coordinates of P’Q’R’ S’.(2 marks)
P’(—2, 2), Q’(—6, 2), R’(—6, 4), S’(—2, 8)
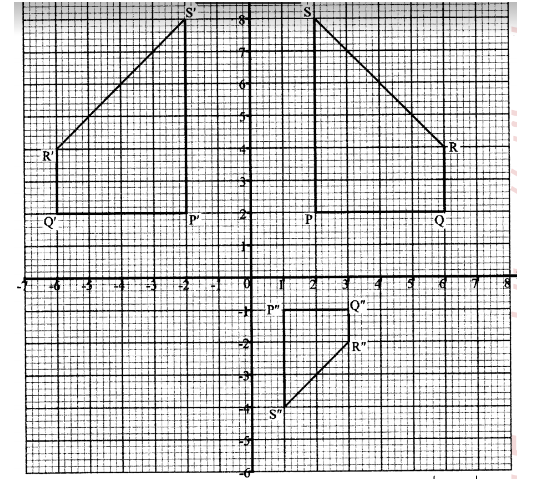
(b) On the grid provided draw PQRS and its image P’Q’R’S’ (2 marks)

(c) Find P”Q”R”S“, the image of P’Q’R’S’ under the transformation matrix. N = (-½/0 0/-½)(1 marks)
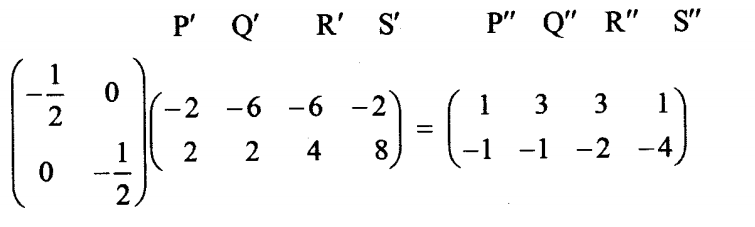
(ii) On the same Grid draw P”Q”R‘S”.(1 marks)
d) (i) The matrix is N-1 (d) (i) Find a single matrix that maps P”Q”R’S” onto P’Q’R’S’.(2 marks)
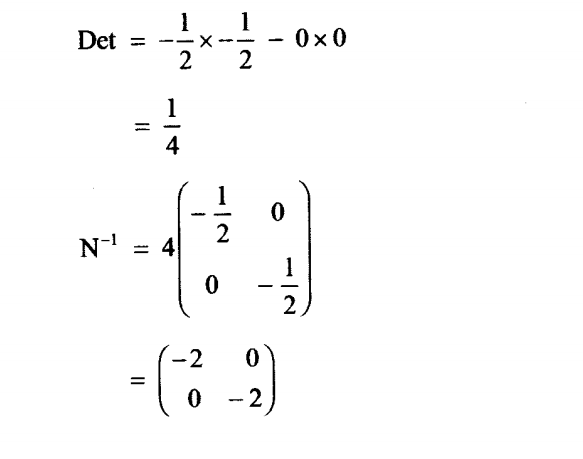
(ii) Describe fully the transformation that maps P”Q”R”S” onto P’Q’R’s’.(2 marks)
S.F =-2<
