
2019 Mathematics Paper 1
Kenya Certificate of Secondary Education
Section I (50 marks)
Answer all the questions in this section.
1. Without using mathematical tables or a calculator, evaluate: 5.4∕ 0.025 x 3.6 (3 marks)
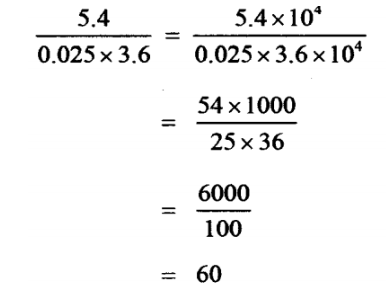
2. Express 1728 and 2025 in terms of their prime factors. Hence evaluate:(4 marks)
∛1728 √ 2025
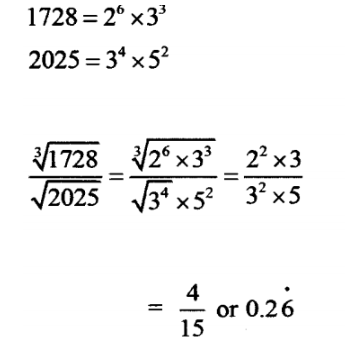
3. Juma left his home at 8.30a.m. He drove a distance of l40km and arrived at his aunt’s home at 10.15 a.m.
Determine the average speed, in km/h, for Juma’s journey.(3 marks)

4. Expand and simplify:
4 (q – 6) + 7 (q — 3).(2 marks)
4(q + 6)+7(q — 3) 4q+ 24 + 7q – 21
= 11q + 3
5. In the trapezium PQRS shown below, PQ = 8 cm and SR = 6 cm.
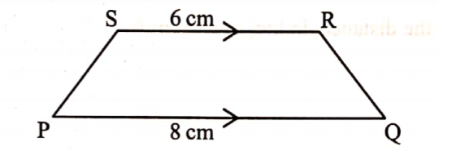
If the area of the trapezium is 28 cm², find the perpendicular distance between PQ and SR. (2 marks)
Area of trapezium = ½(8 + 6)h = 28
7h = 28
h = 4cm
6.Given that = ∛ 94=3n find the value of n.(3 marks)
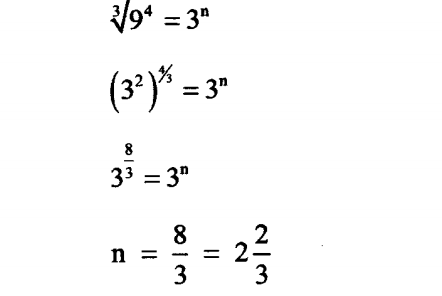
7. Three villages A, B and C rife Such that B is 53 km on a bearing of 295° from A and C IS 75 kin east of B.
(a) Using a scale of 1 cm to represent 10 km, draw a diagram to show the relative positions of villages A, B and C. (2 marks)
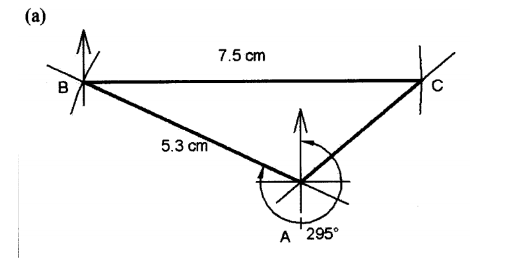
(b) Determine the distance, in km, of C from A. (2 marks)
(b) AC = 3.5cm ± 0.1
AC = (35±1)km
8. A retailer bought a bag of tea leaves. If the retailer were to repack the tea leaves into smaller packets of either 40 g, 250g or 350 g, determine the least mass, in grams, of the tea leaves in the bag.(3 marks)
40 = 2 x 2 x 2 x 5
250 = 2 x 5 x 5 x 5
350 = 2 x 5 x 5 x 7
LCM = 2 x 2 x 2 x 5 x 5 x 5 x 7
= 7000g
9. Given that sin 2x = cos (3z — 10°), find tan z, correct to 4 significant figures. (3 marks)
sin 2s = cos(3s — lO)
2x +(3x —10) = 90
5x = 100
= 20°
tan 20° — 0.3640
10. A tourist converted 5820 US dollars into Kenya Shillings at the rate of Ksh 102.10 per dollar.
While in Kenya, he spent Ksh450 000 and converted the balance into dollars at the rate of Ksh 103.00 per dollar.
Calculate the amount of money, to the nearest dollar, that remained.(3 marks)
$5820 Ksh (5820 H 102.10)
= Ksh 594222
Balance in $
594222 —450000/103.0
144 222/103
1400 US Dollars
11. Given that b =
| (2) |
| (4) |
C,=
| (3) |
| (2) |
and a = 3c — 2b, find the magnitude of a, correct to 2 decimal (4 marks)
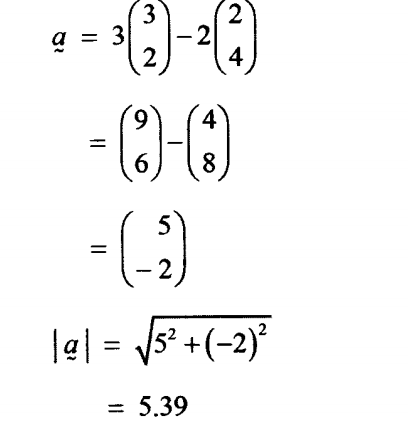
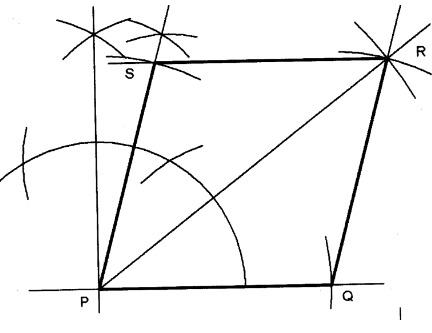
12. Using a ruler and a pair of compass only, construct a rhombus PQRS such that PQ = 6cm and dSPQ = 75°.
Measure the length of PR.
13. Solve the inequality 2x — 1 ≤ 3x + 4 < 7 — x. (3 marks)
2x – 1 ≤ 3x + 4
-5 ≤ x
3x + 4 < 7 — x
4x<3
x=3/4
-5≤x<3/4
14. Given that A = ( 2 3 4 4 ) B, ( X 1 2 3 )
and that AB is a Singular matrix, find the value of x.(3 marks)
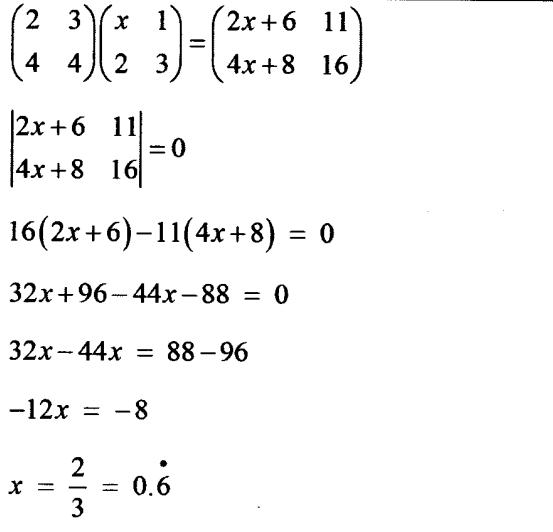
15. A trader bought two types of bulbs A and B at Ksh 60 and Ksh 56 respectively.
She bought a total of 50 bulbs of both types ct a total of Ksh 2872.
Determine the number of type A bulbs that she bought. (3 marks)
A + B = 50
60A + 5dB = 2872
60A + 5d(50-A) — 2872
4A = 2872-2800
4A = 72
A = 18
16. A bus plies between two towns P and R via town Q daily. On each day it departs from P at 8.15 a.m. and stops for 40 minutes at Q before proceeding to R.
On a certain day, the bus took 5 hours 40 minutes to travel from P to Q and 3 hours 15 minutes to travel from Q to R.
Find, in 24 hour clock system, the time the bus arrived at R. (3 marks)
Time taken
5 hours 40 min 3 hours l5 min
40 min 9 hours 35min
Arrival time = 08.15 + 9 hrs 35 min
= 1750 hours
SECTION II (50 marks)
17. A rectangular water tank measures 2.4 m long, 2 m wide and 1.5 m high.
The tank contains some water up to a height of 0.45 m.
(a) Calculate the amount of water, in litres, needed to fill up the tank (3 marks)
(a) Volume of water required
= 2.4 x 2 x (1.5 – 0.45)m³
= 2.4 x 2 x 1.05 m²
Amount of water in litres
= 2.4 x 2 x 1.05 x 1000 litres
= 5040 litres
(b) An inlet pipe was opened and water let to flow into the tank at a rate of 10 litres per minute.
After one hour, a drain pipe was opened and water allowed to flow out of the tank at a rate of 4 litres per minute.
Calculate:
(i) the height of water in the tank after 3 hours;(4 marks)
Amount of water let in by 3h is
= 10 x 3 x 60= 1800 litres
Amount of water drawn from the tank in 2h is
= 4 120 = 480 litres
Total amount of water in tank after 3h
— 2160 +1800 — 480
3480 litres
Height of water in tank is 3480/1000 x 2 x 2.4
0.725 m
(ii) the total time taken to fill up the tank. (3 marks)
Height of water to be filled
= 1.5 — 0.725 — 0.775 m
Time in hours taken to fill the tank is
3h+ (2.4x 2 x 0 775 x1000/6×60)h
3h +10⅓ h
13⅓h(or 13h 20min)
18. (a) A line, L, posies through tho points (3,3) and (5,7).
Find the equation of L, in the form y = mx+c where m and c arc constants. (3 marks)
Gradient
7 — 3/5 —3
= 2
Equation of L1
=y-3/x—3 = 2
y = 2x —3
(b) Another line L2 is perpendicular to L, and passes through (—2, 3). Find:
(i) the equation of L2;
Gradient of L2
i 2 Equation of £2 y – 3/x + 2 = -1
y-3 = -1/2x – 1
y = 1/2x + 2
(ii) the x-intercept of L2.
When y = 0
-1/2 x + 2 = 0
x = 4
The x intercept of L2 is 4
(c) Determine the point of intersection of L, and L2. (3 marks)
(c) At point of intersection of L, and L2
2x – 3 = -1/2x + 2
2½x = 5
x = 2
When x = 2, y —— 2(2) — 3 = I
Point of intersection is (2,1)
19. A triangle ABC with Vertices A (—2,2),B (1,4)and C (-1,4) is mapped on to triangle A’B’C by a reflection in the line y=x+1.
(a) On the grid provided draw
(i) triangle ABC (3 marks)
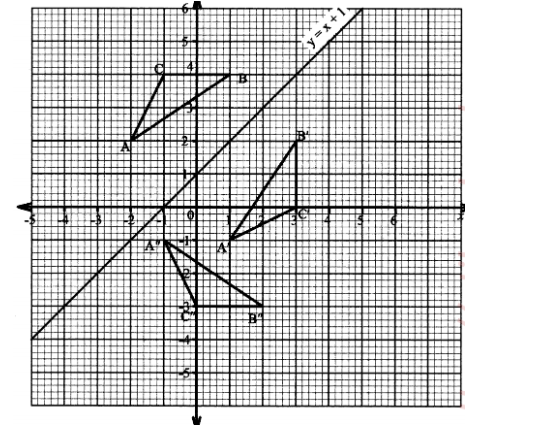
(ii) the line y = x + 1; (2 marks)
(iii) triangle A’B’C’. (2 marks)
(b) Triangle A”B”C“ is the image of triangle A’B’ C’ under a negative quarter turn (0,0).
On the same grid, draw triangle A“B“C“. (3 marks)
20.The figure below is a right pyramid VEFGHI with a square base of 8cm and a slant edge of 20cm Points A B C and D lie on the slant edges or the pyramid such that VA = VB = VC = VD = I0 cm and plane ABCD is paralell to the base EFGH.
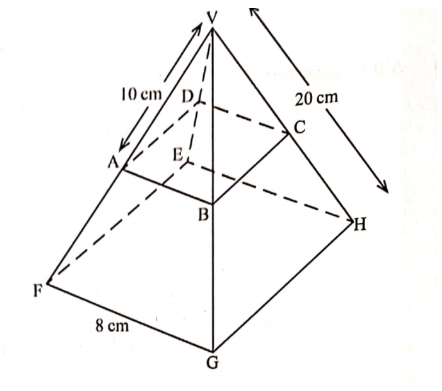
(a) Find the length of AB. (2 marks)
AB/8 = 10/20
AB = 1/2 X 8
= 4cm
(b) Calculate to 2 decimal places
(i) The length of AC (2 marks)
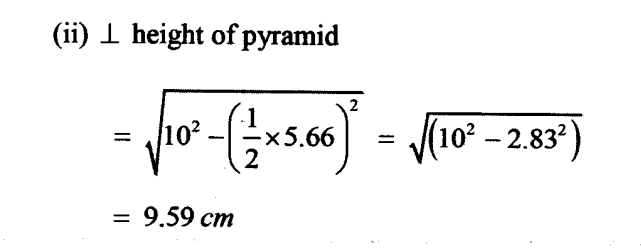
(ii) The perpendicular height of the pyramid VABCD (2 marks)
Volume of VABCD 1/3x 4 x 4x 9.59
= 51.15 cm³
Volume of VEFGH
1/3 x 8x 8x(2 x9.59)
= 409.17
Volume of frustum ABCDEFGH
409.17 —51.15
358.02cm³
(c) The pyramid VABCD was cut off.Find the volume of the frustum ABCDEFGH correct to 2 decimal places (4 marks)
2 +8 +10+ 6+ 2 + z= 40
x = 12
21. The heights of 40 athletes in a county athletics competition were as shown in the table below.
| Height,cm | Frequency |
|---|---|
| 150 -159 | 2 |
| 160 – 169 | 8 |
| 170 – 179 | 10 |
| 180 – 189 | x |
| 190 -199 | 6 |
| 200 – 209 | 2 |
(a) Find the value of X. (1 mark)
2 +8 + 10 + 6+ 2 + x = 40
x = 12
(b) State the modal class. (1 mark)
Modal class = 180 — 189
(c) Calculate:
(i) The mean height of the athletes;(4 marks)
| Height | Mid pt | Freq | fx |
|---|---|---|---|
| 150 – 159 | 154.5 | 2 | 309 |
| 160 – 169 | 164.5 | 8 | 1316 |
| 170 – 179 | 174.5 | 10 | 1745 |
| 180 – 189 | 184.5 | 12 | 2214 |
| 190 – 199 | 194.5 | 6 | 1167 |
| 200 – 299 | 204.5 | 2 | 409 |
| 40 | 7160 |
Mean height = 7160/40
=179
(ii) The median height, correct to 1 decimal place,of the athletes (4 marks)
| x | 0 | 200 | 400 | 600 | 800 | 1000 | 1200 |
|---|---|---|---|---|---|---|---|
| Ordinates along AB | 200 | 240 | 280 | 300 | 280 | 240 | 200 |
| Ordinates along CD | 400 | 500 | 580 | 600 | 580 | 580 | 640 |
Median Height = height of 20th athlete
= 179.5
22. The figure below represents a triangular 8ower garden ABC in which AB = 4 in, BC = 5m and ∠BCA = 30°. Point D lies on AC such that BD = 4 m and ∠BDC is obtuse.
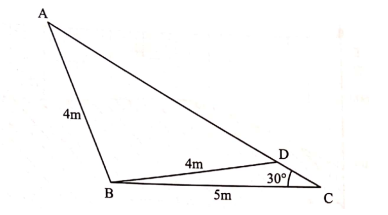
Find, correct to 2 decimal places:
(a) ∠BDC; (3 marks)
(a) Let BDC = 8
Sinθ/5 = _ Sin30°/4
Sin θ = 5 x Sin30/4 = 0.625
Acute θ = 38.68°
Obtuse θ = 141.32°
(b) the length of AD; (3 marks)
Angle ABD = 180 – 38.68 x2
= 102.64
AD² = 4² + 4² – 2 X 4 X 4 cos 102.64
39
AD = 6.24m
(c) the length of DC; (2 marks)
DBC 180 —(30+141.32)
= 8.68°
Using sine rule
Sin 8.68/DC = Sin30/4
DC = 8 Sin 8.68
= l.21m
(d) the area of the flower garden ABC. (2 marks)
1/2x4x5sin(8.68+102.64)
= 9.32 m²
23. The shaded region on the graph below shows a piece of land ABCD earmarked for building a sub-county hospital.
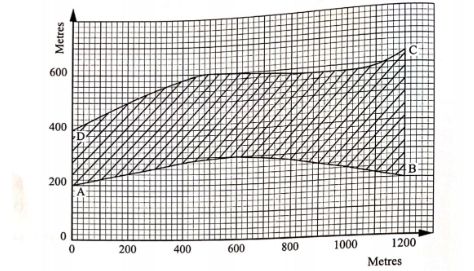
(a) Write down the ordinates of curves AB and DC for x = 0, 200, 400, 600, 800, 1000 and 1200. (2 marks)
| x | 0 | 200 | 400 | 600 | 800 | 1000 | 1200 |
|---|---|---|---|---|---|---|---|
| Ordinates along AB | 200 | 240 | 280 | 300 | 280 | 240 | 200 |
| Ordinates along CD | 400 | 500 | 580 | 600 | 580 | 580 | 640 |
(b) Use trapezium rule, with 6 strips to estimate the area of the piece of land ABCD, in hectares.(4 marks)
Area of piece of land ABCD using trapezium nile Area under curve AB 1/2x 200 {(200+ 200) + 2(240 + 280 + 300 + 280 + 240)}
= 100(400 + 2680)
= 308 000 m²
Area under curve CD
1/2x {200 (400 + 640) + 2(500 + 580 + 600 + 580 + 580)}
= 100 (1040 + 5680)
= 672 000
Area of land ABCD
= 672000 — 308000
364O00m²
364000/10000 ha
36.4 ha
(c) Use mid-ordinate rule with 3 strips to estimate the area of the piece of land, in hectares. (4 marks)
— 400{(500+ 600 +580) —(240 + 300 + 240)}
= 400H 900
360000 m²
360000/10000
= 36ha
24. The equation of a curve is y=x3+x2-x-1
(i) Determine the stationary point of the curve (3 marks)

(ii) the nature of the stationary points in (a) (i) above.(2 marks)
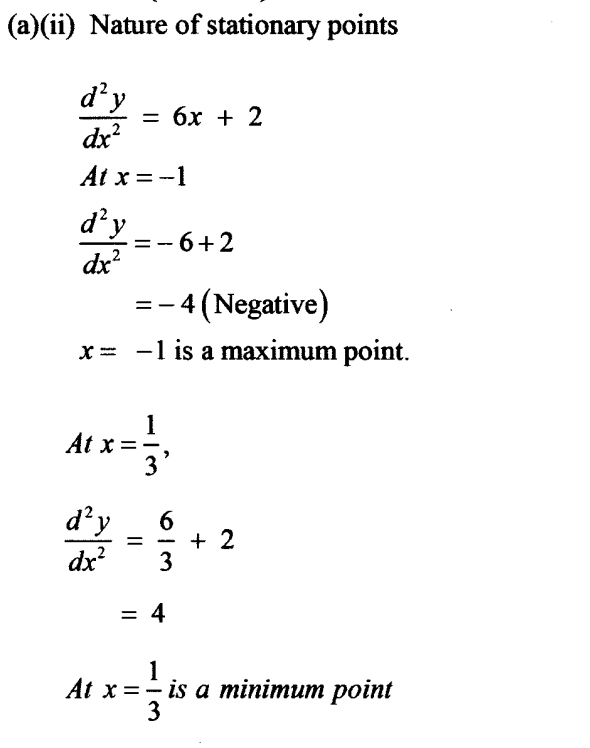
(b) Determine:
(i) the equation of the tangent to the curve at x = 1; (3 marks)
) at x = 1 y = 0
At x = l
dy/dx 3(1) + 2(1) —1 4
Equation of tangent
y —0/x-1 = 4
y = 4x — 4
(ii) the equation of the normal to the curve at x = 1. (2 marks)
Let gradient of normal = m2
m2
x 4 = -4
m2
= – 1/4
y-0/x-1 = -1/4
y = -1/4x – 1/4
