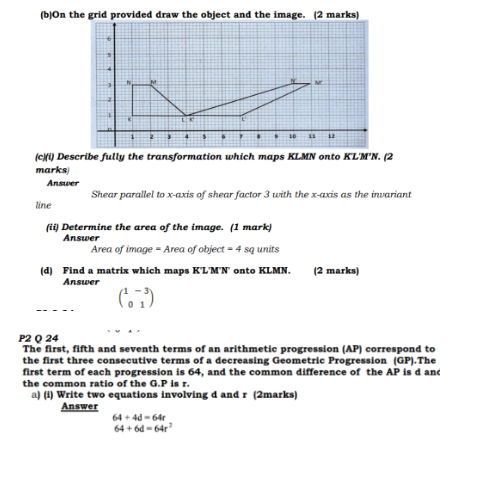
2016 Mathematics Paper 2
1.
7. The masses in kilograms of 20 bags of maize were: 90, 94, 96, 98, 99, 102, 105, 91, 102, 99, 105, 94, 99, 90, 94, 99, 98, 96, 102 and 105.
Using an assumed mean of 96 kg, calculate the mean mass, per bag of the maize. (3 marks)
8. The first term of an arithmetic sequence is —7 and the common difference is 3.
(a) List the first six terms of the sequence; (1 mark)
First six terms -7,-4,-1,2,5,8
(b) Determine the sum of the first 50 terms of the sequence. (2 marks)
Sum of the first 50 terms
50/2 = {2 x -7 + 49 x 3}
332.5
9. A bag contains 2 white balls and 3 black balls. A second bag contains 3 white balls and 2 black balls.
The balls are identical except for the colours. Two balls are drawn at random, one after the other from the first bag and placed in the second bag.
Calculate the probability that the 2 balls are both white. (2 marks)
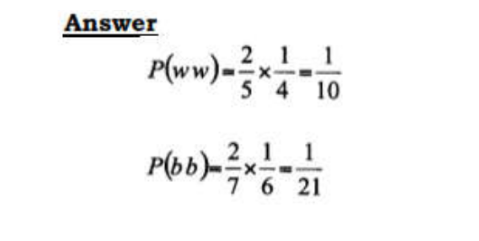
10. An arc 11 cm long, subtends an angle of 70° at the centre of a circle.
Calculate the length, correct to one decimal place, of a chord that subtends an angle of 90° at the centre of the same circle. (4 marks)
- Length 12.7cm11. Given that qi + 1/3j + 2/3k is a unit vector, find q. (2 marks)
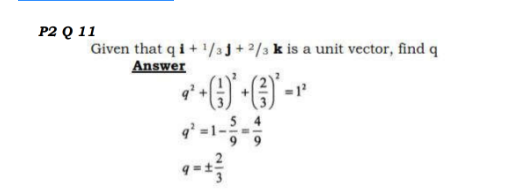
- 12. (a) Expand the expression (1 + 1/2 x)5 in ascending powers of x, leaving the coefficients as fractions in their simplest form. (2 marks)
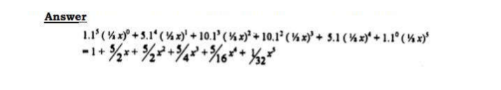
- (b) Use the first three terms of the expansion in (a) above to estimate the value of (1½o)5. (2 marks)
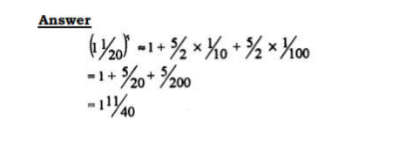
- 13. A circle whose equation is (x – 1)2 + (y – k)2 = 10 passes through the point (2,5). Find the value of k. (3 marks)
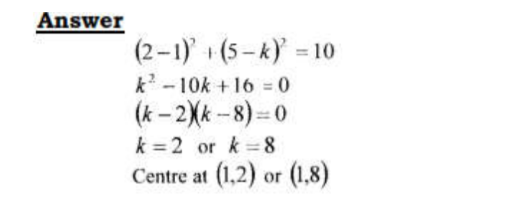
- 14. Water and milk are mixed such that the volume of water to that of milk is 4:1. Taking the density of water as 1 gcm3 and that of milk as 1.2g/cm3, find the mass in grams of 2.5 litres of the mixture. (3 marks)
- 15. A school decided to buy at least 32 bags of maize and beans.The number of bags of beans were to be at least 6.
A bag of maize costs Ksh 2 500 and a bag of beans costs Ksh 3 500. The school had Ksh 100 000 to purchase the maize and beans.
Write down all the inequalities that satisfy the above information. (4 marks)
x + y ≥ 32,x >20,y ≥ 6,5x + 7y ≤ 200
16. Find in radians, the values of x in the interval O’⋜ x ?Πc for which 2 cos2x — sin x = I. (Leave the answer in terms of Π) (4 marks)
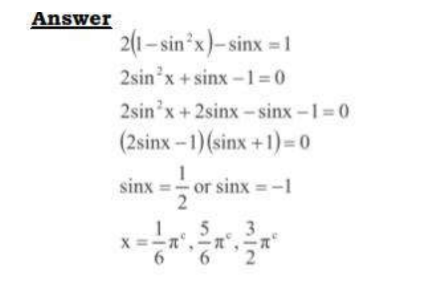
- (b) Calculate the mid-ordinates of 5 strips between x – 1 and x = 6 Use the mid-ordinates rule to approximate, the area under the curve between x-1 ,X = 6 and the x axis.(3 marks)
- (c) Assuming that the area determined by integration to be the actual area,calculate the percentage error in using the mid-ordinate rule.(4 marks)
- 17. A garden measures 10 m long and 8 m wide.A path of uniform width is made all round the garden.
The total area of the garden and the path is 168 m2.
(a) Find the width of the path. (4 marks)
Let the width of the path be x
➡ Area =)(10 + 2x )(8 + 2x) = 168
➡ 80 + 20x + 16x + 4x² = 168
➡ 4x² + 36x – = 0
➡ x² + 9x – 22 = 0
➡(x – 2)( x + 11) = 0
➡ x = 2 or -11
width of the path = 2m
(b) The path is to be covered with square concrete slabs. Each corner of the path is covered with a slab whose side is equal to the width of the path.
The rest of the path is covered with slabs of side 50 cm.
The cost of making each corner slab is Sh 600 while the cost of making each smaller slab is Sh 50.
Calculate:
(i) the number of the smaller slabs used. (3 mark)
14/68 x 12 – {10 x 8 + 4 (2 x2 )}
No. of slabs = 72/0.5 x 0.5
Ans = 288
(ii) the total cost of the slabs used to cover the whole path. (3 marks)
Cost of slabs = Large = 600 x 4 = 2400
Small = 50 x 288 = 14400
Total Cost = 2400 + 14400 = 16,800
18. In the figure below, P, Q, R and S are points on the circle with centre 0. PRI’ and USTV are straight lines. Line USTV is a tangent to the circle at S. L RST = 50° and L RTV = 150°.
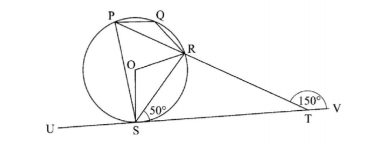
- (a) Calculate the size of(i) L QRS; (2 marks)
(ii) L USP;
(1 mark)
(iii) L PQR. (2 marks)
(b) Given that RT = 7cm and ST = 9 cm, calculate to 3 significant figures: ( ) the length of line PR: (2 marks)
(ii) the radius of the circle. (3 marks)
19. The figure ABCDEF below represents a roof of a house. AB = DC = 12m, BC = AD = 6 m. AE = BF = CF = DE = 5 m and EF = 8 m.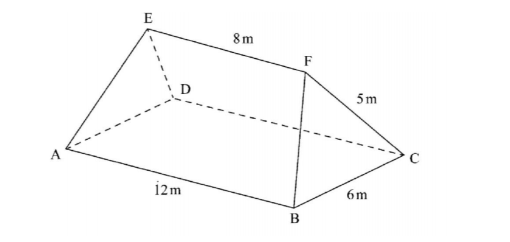
- (a) Calculate, correct to 2 decimal places, the perpendicular distance of EF from the plane ABCD. (4 marks)(b) Calculate the angle between:
(i) the planes ADE and ABCD; (2 marks)
(ii) the line AE and the plane ABCD, correct to 1 decimal place; (2 marks)
(iii) the planes ABFE and DCFE, correct to 1 decimal place. (2 marks)
