Interest rates
Interest rate is the price that a borrower of funds must pay to the lender to secure use of funds for a specified period. An interest rate is a predetermined or negotiated payment made or received for the temporary use of money. A financial institution will charge interest when it lends money to a consumer and a consumer will receive interest when he or she deposits money with a financial institution. It is useful to think of interest as the rental charge on money.
4.1 The fisher effect
In economics, interest is considered the price of credit, therefore, it is also subject to distortions due to inflation. The price of a loan or credit card statement is reflected by nominal interest rate. The nominal interest rate is the interest rate you hear about at your bank. If you have a savings account for instance, the nominal interest rate tells you how fast the number of shillings in your account will raise over time. This nominal interest is composed of the real interest rate plus inflation, among other factors. The real interest rate
corrects the nominal interest rate for the effect of inflation in order to tell you how fast the purchasing power of your savings account will rise over time. A simple formula for the nominal interest is: , Where i is the nominal interest, r is the real interest and π is inflation. This relationship between nominal interest rate, real interest rate and inflation is known as the fisher hypothesis, fisher parity or fisher effect. Fisher effect is a proposition by Irving Fisher that the real interest rate is independent of monetary measures,
especially the nominal interest rate. The Fisher equation is represented as follows for compounded interest rate
This equation implies that the real interest rate (r) equals the nominal interest rate (R ) minus expected inflation rate (πЄ). In the case of simple rates, the Fisher equation takes a different form as shown below: If r is assumed to be constant, R must rise when πЄ rises. Thus, the Fisher Effect states that there will be a one for one adjustment of the nominal interest rate to the expected inflation rate. From the equation it can be deduced that:
- Real interest rate = Nominal Interest Rate – Expected Inflation Rate
- Nominal Interest Rate = Real interest Rate + Expected Inflation Rate
The fisher effect has the implication that if inflation permanently rises from one constant level to a higher constant level that currency’s interest rate would eventually catch up with the higher inflation, rising by same points as inflation year from their initial level. These changes leave the real return on that currency or financial assets unchanged.
In the Macroeconomic policy plane, the Fisher effect is evidence that in the long-run, purely monetary developments will have no effect on that country’s relative prices
4.2 Interest Rates and Discount Rates
The interest rate that is used in making present-value calculation is often called the discount rate. The process of taking present values is often called discounting or reducing future payments to their current value. It is also important to understand another known as yield which is normally used for interest rate. Yield is a term which is generally used to describe the return on holding a bond. So, interest rate, discount rate, yield all essentially mean the same thing. The concepts of an interest rate and a discount rate are important when making financial decisions. Everyone makes the same basic decisions about their income: how much to consume and how much to save. One simple thing is true, people who are more patient tend to save more. These people tend to value the future more. This is the same as saying they discount the future less, or payments in the future have higher present values.
Thus, these people will save in the presence of lower interest rates. All assets and financial markets offer interest rates for holding saving. If an interest rate exceeds a person’s discount rate, then it is likely that they will choose to participate in the market.
4.3 Applying Present Value
Present value is a very important concept in financial decision making. It is important that we go through a few examples to show how to use this concept. These examples entail not only how to compute the present value of a single future payment, but also for a stream of future payments by stringing together several present value computations.
Internal Rate of Return
Internal Rate of Return is the interest rate which equates the present value of an investment with its cost. The following example clearly depicts the usefulness of this concept. One common use of present value is to help make investment decisions.
Suppose we have the following example. You are a business owner deciding whether to buy a new machine. The seller of the machine says that it costs $100,000. We analyze the usefulness of the machine and find that the machine will generate an extra $30,000 for the next 4 years. After 4 years the machine will be obsolete and can no longer be used. Should you buy the machine? Answer: Maybe. If the business owner takes out a loan of $100,000 to cover the cost of the machine, will the $30,000 in extra revenues cover the
loan payments? If the extra revenue does cover the loan payments with a little extra, then yes buying the machine is a good idea, otherwise he had better not buy it. So, we need to figure out if the revenue stream from the machine is high enough to cover the expenses. To do this we need to calculate the internal rate of return on the machine. Denoting the internal rate of return (IRR) of
this machine as i internal rate of return of the machine is obtained through the following formulae:
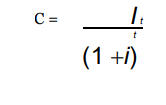
Where It is the expected future cash inflows from the machine, C is the cost of the machine, i is the internal rate of return while t is the time period. In a typical problem with four equal annual expected cash inflow, then t=4. The formulae above is simplified to:

By simple algebra manipulation, this becomes a polynomial of order four which can be easily solved .It turns out that if i = 0:07714. Both sides of the above equation equal $100,000. So the internal rate of return for this machine is 7.714%. The decision criteria involve comparing this rate with the market rate of lending. If the lending rate is less than the IRR, then the project or investment is profitable.
4.4 Valuation of a Bond
One of the basics of finance is to use present value calculation to compute the value of bonds. A Bond is a promise to make a series of payments on specific future dates. Depending on the type of bond, the number of timing of the payments will change. We are going to begin by looking at some of the most common types of bonds. The first is called a coupon bond. Say a borrower wishes to borrow $100 by issuing a coupon bond. This is done by selling the bond to a lender who gives the borrower $100 in return for the bond. The
borrower is required to make annual payments called coupon payments.
These payments depend on the interest rate tied to these bonds called the coupon rate. Thus if this is 5% coupon bond, the borrower would be required to pay 5% of the total amount borrowed to the lender every period. Thus the lender would receive a yearly payment of $5 in this example. A bond will also specify when the initial principal is to be repaid. This is the maturity date of the bond. So, how much should someone be willing to pay for this kind of contract. The answer is the present value of the bond which is a sum of two
values: the present value of the future principal payment and the present value of a stream of coupon payments.
Example
Suppose we have the opportunity to buy a $1000 coupon bond with a maturity of 30 years and an interest rate of 6%.
Solution
PV= PVF +PVCP, Where PVF is the present face value of the bond and PVCP is the present value of the coupon payments. In mathematical notation we can write,

The present value of the bond is equal to the face value of the bond, this will occur if the coupon rate equals the interest rate. This doesn’t have to be the case. The coupon rate (which is specified in the bond) can differ from the interest rate/discount rate. If the interest rate is 5%? the present value of this bond will be $1153.73. The bond is worthy holding.
4.5 Value of a stock or a share
A share is bought with expectation of some dividends and capital gains after exchange of ownership. The value of a share is obtained by computing the present value of expected dividends and disposal price
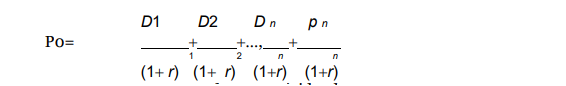
Where Di is the expected annual dividend payment and r is the interest rate. In this model we are assuming that the specific time for selling of the share is known but this might not be the case always. The investor may hold the asset for a long period and at the same time, the dividend value may be growing overtime. Assuming a constant growth rate g, then the price of a share can be expressed as:
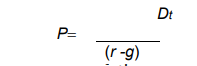
This relationship is called the dividend-discount mode
