
MAASAI MARA UNIVERSITY
REGULAR UNIVERSITY EXAMINATIONS
2015/2016 ACADEMIC YEAR
THIRD YEAR FIRST SEMESTER
SCHOOL OF BUSINESS & ECONOMICS
BACHELOR OF ECONOMICS
COURSE CODE: ECO 314
COURSE TITLE: QUANTITATIVE METHODS I
DATE: 6TH MAY 2016 TIME: 11-1 PM
INSTRUCTIONS TO CANDIDATES
Answer Question ONE and any other THREE questions
This paper consists of 4 printed pages. Please turn over.
QUESTION ONE (25 MARKS)
A manufacturer produces three products X, Y and Z. During production, the products require the use of two machines, A and B. The number of hours neeeded on both machines are shown in the following table

Machine A and B can be used for 40 hours and 34 hours a week respectively. the profits per unit is sh 10, sh 15 and sh 22 for product X , Y and Z respectively.
Formulate the linear Programing problem (3 Marks)
Solve the linear programming problem in a) above (12 Marks)
State and explain the assumptions for the input-output models (6 Marks)
Determine the functional dependence of the following functions
Y_1=〖3x〗_1^2+〖2x〗_2^2
Y_2=〖5x〗_1+1 (4 marks)
QUESTION TWO (15 MARKS)
Differentiate the following terms
Mutually exclusive Events and collectively Exhaustive events (2 marks)
Sample space and experiment (2 Marks)
Solve the following three simultaneous equations using the gaussian method.
2X+12Y-2Z=20
2X+3Y+3Z=17
3X-3Y-2Z=-9 (8 marks)
Differentiate the three approaches to probability (3 marks)
QUESTION THREE (15 MARKS)
Given the linear programing problem below, form its dual problem
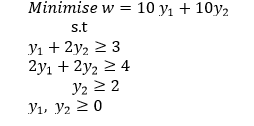
250 members of a certain society have voted to elect a new chairman. Each member may vote for either one or two candidates. The candidate elected is the one who polls most votes. Three candidates x, y z stood for election and when the votes were counted, it was found that:
59 voted for y only, 37 voted for z only
12 voted for x and y, 14 voted for x and z
147 voted for either x or y or both x and y but not for z
102 voted for y or z or both but not for x
Required
Express the above information in a venn diagram (3 marks)
What is the probability that voters voted for x only? (2 marks)
What is the probability that voters voted for y? (2 marks)
What is the probability that voters voted for z? (2 marks)
What is the probability that a voter did not vote? (2 marks)
QUESTION FOUR (15 MARKS)
Out of 3000 tires in a warehouse, 2000 are domestic and 1000 are imported. Among the domestic tires, 40 % are all season and for the imported tires, 10% are all season. If a tire is selected at random and it is all-season, what is the probability that it is imported. (4 marks)
the IQs of a large population of children are normally distributed with a mean of 100.4 and a standard deviation of 11.6.
what percentage of children have IQs greater than 125?
(4 Marks)
90% of the children have IQs greater than what value?
(3 marks)
A commitee has 7 members, 3 men and 4 women. In how many ways can a sub commitee of four be selected if it is to consist of exactly
Three men (1 Mark)
Four women (1 Mark)
Two men and Two women (2 Mark)
QUESTION FIVE(15 MARKS)
The input-output ratio coefficients for a three sector economy are given as:
Determine the total output required in each of the three sectors to meet the inter-industry input requirements and the final demand. (9 marks)
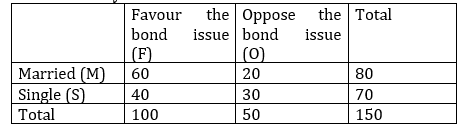
In a survey of 150 people, each person was asked his/her marital status and their opinion about floating a bond issues to build a community centre. The results are summarised as follows

Find the probability that
A person favours the bond issue, given that the person is married (3 marks)
A person is married, given that the person favours the bond issue (3 marks)
