
MAASAI MARA UNIVERSITY
REGULAR UNIVERSITY EXAMINATIONS
2018/2019 ACADEMIC YEAR
SECOND YEAR, FIRST SEMESTER
SCHOOL OF BUSINESS AND ECONOMICS
BSC. AGRICULTURAL ECONOMICS AND RESOURCE MANAGEMENT
COURSE CODE: ECO 2204
COURSE TITLE: MATHEMATICS FOR
ECONOMISTS II
DATE: 11TH DECEMBER, 2018 TIME: 1100 – 1300 HRS
INSTRUCTIONS TO CANDIDATES
Answer Question ONE and any other THREE questions
This paper consists of 4 printed pages. Please turn over.
QUESTION ONE
a) Find the derivatives of y with respect to x:


QUESTION TWO
a) Given Demand and Supply functions in a one-commodity market
model as:

QUESTION THREE
a) Wijenje has the following maize production function
![]()
Where Q is the quantity of maize produced while K and L are
units of inputs capital and labour respectively. Supposing that
the prices of K and L are Ksh 20 and Ksh. 40 respectively, and
that he has a total of Ksh. 5000 to spend on the two inputs:
i. Using Lagrangean optimization technique determine the values of
λ, K and L at profit maximization level
ii. What will be Wijenje’s maximum profit
iii. Using bordered Hessian matrix, confirm that the critical values
present a maximum (15 marks)
QUESTION FOUR
a) Noellene is a price discriminating monopolist having the following
functions for her milk production firm:
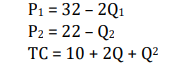
Determine the prices and quantities for the milk in the two different
markets (9 marks)
b) The following demand and supply functions were extracted from a
perfectly competitive market

Q supply function
Determine Producer Surplus and Consumer Surplus at equilibrium
(6 marks)
QUESTION FIVE
a) What is the usefulness of the Lagrangean multiplier in mathematical
optimization (3 marks)
b) Faith has a mango firm in Kitui in which she has an objective of:
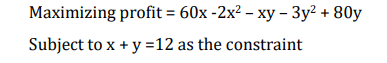
i. Compute the values of x, y and λ at profit maximization
point (10 marks)
ii. What will be Faith’s profit (2 marks)
