
MAASAI MARA UNIVERSITY
REGULAR UNIVERSITY EXAMINATIONS 2013/2014 ACADEMIC YEAR
SECOND YEAR SECOND SEMESTER
SCHOOL OF BUSINESS AND ECONOMICS
BACHELOR OF ARTS IN ECONOMICS
COURSE CODE: ECO 210
COURSE TITLE: BASIC MATHEMATICS
DATE: 22ND APRIL, 2014 TIME: 9.00AM – 12.00PM
INSTRUCTIONS TO CANDIDATES
Question ONE is compulsory
Answer any other TWO questions
This paper consists of 4 printed pages. Please turn over.
QUESTION ONE

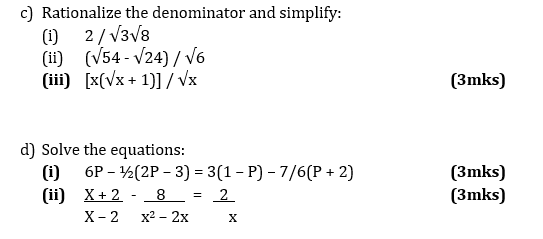
e) Given the arithmetic sequence:
4, 11, 18…….
Find:
i. The common difference.
ii. The 6th term (4mks)
QUESTION TWO
a) List the members of the following sets.

QUESTION THREE
a) Differentiate the following functions with respect to x. (6mks)
(i) Y = x4
(ii) f(x) = 5×3 + 2×2 + x + 7
b) A fridge manufacturer produces and sells all the fridges he produces. The total cost of producing x fridges is 300x + 200. The price demand function is estimated as 500 – 2x.
Determine:
i. The revenue function of the manufacturer. (3mks)
ii. The profit function. (3mks)
iii. The marginal profit function. (3mks)
QUESTION FOUR
a) Solve and graph the following
(i) 7 – 2x > -11 xCR (3mks)
(ii) -5x + 4 < 2x – 10 xCZ (3mks)
b) Solve the equations:
i. 8x – 6 = 5x + 9 (3mks)
ii. 3x + 34 – 8x = 11 – 9x – 13 (3mks)
c) Solve the equations
(i) 2x = 4y = -2
(ii) 5x + 4y = 33 (3mks)
QUESTION FIVE
a) A two digit number is such that its value equals four times the sum of its digits. If 27 is added to the number, the result is equal to the value of the number obtained when the digits are interchanged. What is the number? (6mks)
b) In a survey of 260 college students, the following data is obtained.
64 students – Maths
94 students – Computer Science
58 students – Business Studies
28 students – both Maths and Business English
26 students – both Maths and Computer
22 students – both Computer Science and Business English
i. How many students in the survey did not take any of the three courses? (5mks)
ii. How many students took computer science only?(4mks)
