
MAASAI MARA UNIVERSITY
REGULAR UNIVERSITY EXAMINATIONS
2016/2017 ACADEMIC YEAR
FIRST YEAR SECOND SEMESTER
SCHOOL OF BUSINESS AND ECONOMICS
BACHELOR OF SCIENCE IN ECONOMICS, ECONOMICS AND STATISTICS & FINANCIAL ECONOMICS
COURSE CODE: ECO 1205
COURSE TITLE: ECONOMIC STATISTICS II
DATE: 16TH MAY 2017 TIME: 0830-1030HRS
INSTRUCTIONS TO CANDIDATES
Answer Question ONE and any other THREEquestions.
This paper consists of 5 printed pages. Please turn over.
Question One
(a) You roll one red die and one green die. Define the random variables X and Y as follows: X = The number showing on the red die Y = The number of dice that show the number six For example, if the red and green dice show the numbers 6 and 4, then X = 6 and Y = 1.
i) Write down a table showing the joint probability mass function for X and Y, find the marginal distribution for Y. (4mks)
ii) Compute E(Y). (3mks)
(b) Suppose we want to find a proportion of students who would like to visit the National library. We sampled 100 students and found that 90% of them would like to visit the library. Construct interval confidence of 95% for the population proportion of students. (4mks)

(d) Suppose that a box contains 10 balls which are distributed as follows: three are white and dotted balls, one is white and stripped, two are gray and dotted and four are grey and stripped. Find;
(i) The probability of getting a dotted ball given that its white (2mks)
(ii) The probability of a stripped ball given that its whit (2mks)
(iii) Probability that its grey given that its dotted (2mks)
(iv) Probability that its grey given that its stripped (2mks)
Question Two
(a) Write short notes on the following
(i) Properties of the Chi-Square Distribution (3mks)
(ii) Type I and Type II error (2mks)
(iii) Statistical inference (2mks)
(b) Suppose we are provided with the following information concerning the dependence of the colour of the son’s eyes to the colour of the father’s eyes.
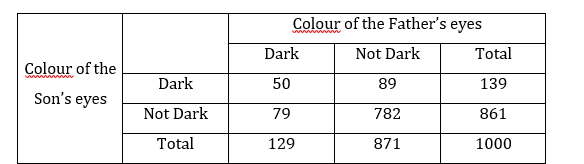
Is the colour of the Son’s eyes independent of the Father’s eyes? (8mks)
Question Three
(a) The Gaussians distributions (Normal distribution) for random variables tend to have density curves that resemble one another in their physical condition. Explain in details the five main properties underlined in the General Normal Distribution. (5mks)
(b) The monthly food expenditure for a single adult meal at Maasai Mara University has a mean of ksh 480 and a standard deviation of ksh 115. If a random sample size of 60 is drawn using this population, what is the probability that mean expenditure in the sample;
i) Lies between 460 and 510 (3mks)
ii) Exceeds 500 (2mks)
(c) Consider a case in which ∏ ≠ 0.5. suppose we toss a die four times, find the number of proportion distribution in which heads appears as follows;
(i) b(0, 4, 1/6) (2mks)
(ii) b(2, 4, 1/6) (2mks)
(iii) b(1, 4, 1/6) (1mks)
Question Four
(a) If a manufacturer of panadol tablets asserts that approximately 40% of the total population uses panadol. A sample of 49 people was taken from a population of those using panadol; the proportion of those using panadol is 18. Is the proportion of people using panadol significantly different from the hypothesized population? (5mks)
(b) Suppose we want to know whether fertilizers significantly increase output. We take a sample of 40 fields and we find that the average yield is 50. We take another sample of 40 fields and the average yield is 45. Given the variance for the first field δ21=100 and second sample is δ22=64. Do fertilizers significantly increase output? (5mks)
(c) Describe the main criterion used in judging estimations in economic statistics . (5mks)
Question Five
(a) A component is tested but the test is not infallible. If the component is good 70% of the time test gives positive indication i.e. 70% of the time test gives positive indication. If the component is defective, 80% of the time test gives negative indication denoting that the system is bad. If in the manufacturing process, the percentage of defective component is 20, calculate;
(i) Probability that the component is good, and test gives positive indication (2mks)
(ii) Probability that the component is good, and test gives negative indication (2mks)
(iii) Probability that the component is not good, and test gives positive indication (1mks)
(iv) Probability that the component is not good, and test gives negative indication (1mks)
(b) Write brief notes on the following aspects as used in economic statistics
(i) Significance of the Central Limit theorem (3mks)
(ii) Probability under statistical independence (3mks)
(iii) Properties of Standard Normal Distribution (3mks)
