
UNIVERSITY EXAMINATIONS: 2016/2017
SUPPLEMENTARY EXAMINATION FOR THE DIPLOMA IN BUSINESS
TECHNOLOGY
DIT401 PROBABILITY AND STATISTICS
DATE: AUGUST 2017 TIME: 1 ½ Hours
INSTRUCTIONS:Answer any THREE questions.
QUESTION ONE
(a) Define skewness and distinguish between positive and negative skewness.
(4marks)
(b)The following data relate to the profits of 1000 companies:-
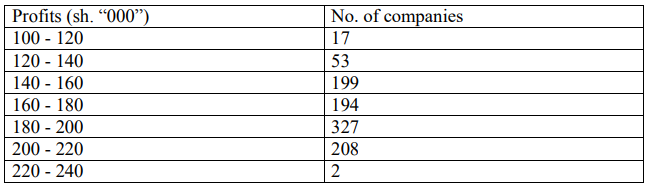
Calculate the Kelly’s coefficient of skewness and comment on its value. (10marks)
(c) The first four central moments of a distribution are 0, 4, 10 and 46
respectively. Compute the moment coefficients of skewness and kurtosis and
comment upon the nature of the distribution (6marks)
QUESTION TWO
(a) If 20% of the bolts produced by a machine are defective, determine the
probability that out of 4 bolts chosen at random:
i. 1 will be defective (4marks)
ii. 0 will be defective (4marks)
iii. Less than 2, will be defective (4marks)
(b)On a statistics examination the mean was 78 and the standard deviation was
10.
i. Determine the standard scores of two students whose grades were 93 and 62,
respectively. (4marks)
ii. Determine the marks of two students whose standard scores were -0.6 and
1.2, respectively. (4marks)
QUESTION THREE
(a) The mean length of 500 laurel leaves from a certain bush is 151mm and the
standard deviation is 15mm. assuming that the lengths are normally
distributed, find how many leaves measure:
(i) Between 120 and 155mm (4marks)
(ii) More than 185mm (4marks)
(b)The following data give the test scores and sales made by nine salesmen
during the last one year.
Test scores 14 19 24 21 26 22 15 20 19
Sales (sh. Millions) 31 36 48 37 50 45 33 41 39
Obtain:
i. The regression equation of test scores on sales (4marks)
ii. The regression equation of sales on test scores and (4marks)
iii. The Pearson’s coefficient of correlation (4marks)
QUESTION FOUR
a) State the features of a probability density function

QUESTION FIVE
(a) Distinguish between empirical probability and theoretical probability.
(4marks)
(b)10% of the tools produced in a certain manufacturing process turn out to be
defective. Find the probability that in a sample of 10 tools chosen at random,
exactly two will be defective by using:
(i) The Binomial distribution. (4marks)
(ii) The Poisson approximation to the Binomial distribution. (4marks)
(c) Let X1,X2, …Xn be i.i.d. random variables that follow Bernoulli distribution
with parameter P. Find moment generating function of X. (4marks)
(d)Let X be a Poisson random variable with parameter . Find the moment
generating function.
