
UNIVERSITY EXAMINATIONS: 2016/2017
EXAMINATION FOR THE DIPLOMA IN INFORMATION TECHNOLOGY
DIT401 PROBABILITY AND STATISTICS
DATE: AUGUST, 2017 TIME: 1 ½ HOURS
INSTRUCTIONS: Answer Question One & ANY OTHER TWO questions.
QUESTION ONE
a) Differentiate between the following terms as used in statistics
i. Qualitative and quantitative variables
ii. Population and sample
iii. Discrete and continuous variables
(9 Marks)
b) The number of points scored in each game by a college team were recorded as follows.
Points scored Matches
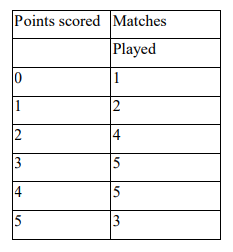
Calculate
i. Mean (3 Marks)
ii. Mean absolute deviation (3 Marks)
iii. Variance (3 Marks)
iv. Standard deviation (3 Marks)
c) A certain data set was collected on a random variable x and the following summaries made:
= 260 and = 2670
Find
i. The mean (4 Marks)
ii. The standard deviation (4 Marks)
QUESTION TWO
a) Find the correlation coefficient by karlpearson’s method between x and y and interpret its value
(4 Marks)
b) Births in a hospital occur randomly at an average rate of 1.8 births per hour. What is the
probability of observing 4 births in a given hour at the hospital? (4 Marks)
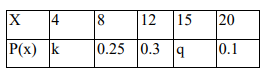
c) The table below gives the probability distribution of a discrete random variable x. Given that
p(x<13) = 0.75, find the value of k and q hence calculate e(x) (4 Marks)
d) The probability that i hit a target is , and the probability that b hits the target is . Both shoot
at the target. Find the probability that
(i) At least one of them hits the target. (3 Marks)
(ii) Neither hits the target (2 Marks)
e) The probability that a student owns a computer is 0.65 and the probability that a student owns a
phone is 0.82. If the probability that a student owns both is 0.55. What is the probability that a
given student owns either a phone or a computer (3 Marks)
X 4 8 12 15 20
P(x) k 0.25 0.3 q 0.1
QUESTION THREE
a) In a class with 10 girls and 20 boys, the following are to be randomly chosen class officials;
class spokesperson and class welfare officer. What is the probability that the two of the
officials are girls? (2 Marks)
b) The weight of 8 diploma students were taken in variable x as they reported and the following
results calculated. (6 Marks)
∑ x = 440 and ∑x2 = 24592
Calculate
i) The mean (3 Marks)
ii) The Variance (3 Marks)
iii) The standard deviation (3 Marks)
c) A class has 10 boys and 5 girls, three students are selected at random. Using a tree diagram,
find the probability that:
i) All are girls (3 Marks)
ii) First 2 are boys (3 Marks)
iii) First and third are of the same sex and the second of opposite sex (3 Marks)
QUESTION FOUR
a) In a study of the daily production of a company over 50 days, the following data was obtained
b) Using a suitable assumed mean, calculate the mean and standard deviation of this data.
(14 Marks)
c) In a bag of 40 vegetables, 25 are carrots and 15 are potatoes. The mean weight of the carrots
is 60grams while that of the potatoes is 52 grams. The standard deviations of the weights arc 4
grams and 6 grams for the carrots and potatoes, respectively. Calculate the mean and standard
deviation of all the vegetables in the bag. (6 Marks)
65 76 36 48 49 48 84 55 79 51
43 21 78 35 37 61 40 45 68 34
88 45 50 53 60 34 56 67 57 42
59 62 62 65 76 55 74 61 70 73
35 41 60 74 52 82 63 58 32 26
QUESTION FIVE
a) The following is data on the heights, in meters, of trees in a certain forest
31 51 37 41 68 50 32 60 53 45 64 54
53 83 52 55 73 55 66 75 57 59 48 70
71 40 53 47 48 36 45 34 26 72 25 29
18 43 48 26 72 15 36 27 39 50 69 32
Prepare a grouped frequency distribution and find the mean of the
grouped data ( 15 Marks)
b) In a company there are 10 managers and 6 accountants. 6 managers and 3 accountants are
female, find the probability that a person selected at random is a. (5 Marks)
